AVL树 (树ADT连载 4/13)
可在作者的 github仓库 中获取本文和其他文章的 markdown 源文件及相关代码。
欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题,我将长期维护所有文章。
所有文章均用 Typora 完成写作,可使用 Typora 打开文章 md 文件,以获得最佳阅读体验。
🌲🌲🌲 一起手写一棵完整的 AVL 树。
❗️ 【NEW】 ❗️
这是小白 yuki 推出的「树ADT」系列文章的第 4 篇 (4/13) 。
k e y w o r d s keywords k ey w or d s
AVL树 / 单旋转与双旋转 / 绝对平衡
本文介绍一种最早提出的自平衡二叉查找树 –– AVL树。本文重点在于展现如何设计一个AVL树类,分析主要方法的代码实现,并给出该类的完整实现代码。期待读者学习之后 能够自己写出一个方法较为完备的AVL树类 。
yuki的其他文章如下,欢迎阅读指正!
如下所有文章同时也在我的 github 仓库 中维护。
[2022-10-17]
旋转后结点高度更新代码有误,Math.max() 取得左右子树中较高者的高度后还要加 1。感谢匿名用户提醒!🙏
[TOC]
AVL树
对于二叉查找树的插入、删除、查找等操作,时间复杂度为 O ( l o g n ) O(logn) O ( l o g n ) 保持树的平衡 ,即保持树的高度为 l o g n logn l o g n 二叉查找树 一文的删除结点的操作中,我们总是 删除目标结点右子树中的最小结点 ,可以预见多次删除操作后将使树呈现 左高右低的倾向 。而一旦树不平衡,插入、删除、查找等操作将无法达到 O ( l o g n ) O(logn) O ( l o g n ) 平衡 BST 。 AVL 树是最早提出的自平衡二叉查找树 。
AVL 树以 「旋转 (rotation)」 操作保证 任意结点的左右子树高度差不超过 1 ,使得树的深度总保持为 O ( l o g n ) O(logn) O ( l o g n )
AVL (Adelson-Velsky and Landis Tree) 树由 G.M. Adelson-Velsky 和E.M. Landis于1962年的 论文 中首次介绍。
文本内容为 Mark Allen Weiss 所著 数据结构与算法分析:Java语言描述 相关章节的整理和总结。代码亦来自该书,略作改动。
旋转
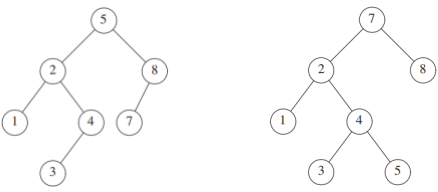
在上图 AVL 树中插入 6 时, 6 将作为 7 的左子结点被插入,这将破坏结点 8 的平衡 (8的左子树与其右子树高差为 2)。AVL 树通过旋转操作能够恢复失衡结点的平衡,本节详细讲解此操作的细节。
考虑插入一个结点 x x x y 1 , y 2 , … y1, y2,… y 1 , y 2 , … x x x 只需沿着此路径恢复平衡即可 。更进一步地,不难证明,只需在第一个平衡被破坏的结点 y y y x x x
插入情况必为如下四情形种之一:
1 2 3 4 情形1(左-左): 插入点在 y 的左儿子的左子树 情形2(左-右): 插入点在 y 的左儿子的右子树 情形3(右-左): 插入点在 y 的右儿子的左子树 情形4(右-右): 插入点在 y 的右儿子的右子树
其中 1 和 4,2 和 3 关于 y y y 单旋转 恢复平衡,对于发生在内侧的情况 (左-右,右-左) ,需要通过 双旋转 恢复平衡。
许多资料将本节介绍的左单旋、右单旋、左右双旋、右左双旋分别称作 zag, zig, zag-zig, zig-zag 操作。zig 和 zag 原意并无左右之分,为了避免歧义,本文不采用这种称呼,读者只需了解即可。在「伸展树」一节中还会有「一字型」的左左双旋和右右双旋,分别被称为 zag-zag 和 zig-zig ,也仅需了解即可。
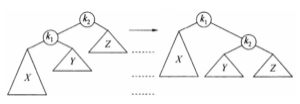
单旋转 右单旋转 (情形1): 如下,左侧的树是在 k 2 k2 k 2 k 1 k_1 k 1 k 2 k2 k 2 k 2 k2 k 2
上左图中 X X X Y Y Y Z Z Z Y Y Y X X X Y Y Y Z Z Z k 1 k1 k 1
单旋转操作方法:
在失衡结点 k 2 k2 k 2 k 1 k1 k 1 k2.left = k1.right,k1.right = k2 ,可以形象地描述为将 k 1 k1 k 1 k 2 k_2 k 2 Y Y Y k 2 k2 k 2 右单旋转 。旋转后以 k 2 k2 k 2 k 1 k1 k 1 h e i g h t height h e i g h t A v l N o d e AvlNode A v lN o d e
1 2 3 4 5 6 7 8 private AvlNode<E> rotateRight (AvlNode<E> k2) { AvlNode<E> k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; k1.height = Math.max(height(k1.left), height(k1.right)) + 1 ; return k1; }
如图调整,将 k 1 k1 k 1 X X X Y Y Y Z Z Z X Y Z XYZ X Y Z
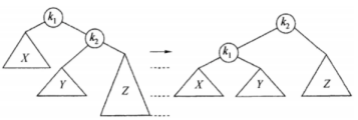
左单旋转(情形4): 如下,左侧的树在 k 1 k1 k 1 k 2 k_2 k 2 k 1 k1 k 1 k 1 k1 k 1
恢复平衡的旋转操作与左-左单旋转类似,核心操作为 k1.right = k2.left,k2.left = k1 。旋转方向为左侧,即逆时针方向,且只有一次旋转操作,因此称为 左单旋转 。以下给出右-右单旋转的代码实现。
1 2 3 4 5 6 7 8 9 private AvlNode<E> rotateLeft (AvlNode<E> k1) { AvlNode<E> k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = Math.max(height(k1.left), height(k1.right)) + 1 ; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; return k2; }
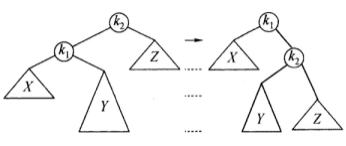
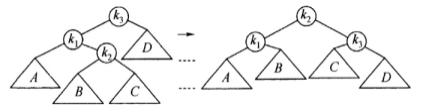
双旋转 左右双旋转(情形2): 如下图左侧的树,在 k 2 k2 k 2 k 1 k1 k 1 k 2 k2 k 2 k 2 k2 k 2
对于情形2和情形3,单旋转无法恢复平衡。如下图,执行一次单旋转后 k 1 k1 k 1 「双旋转」 操作。
双旋转操作方法:
将上述左-右失衡情形 (情形2) 表示为下图。导致失衡的结点插入位置为 k 1 k1 k 1 k 2 k2 k 2
如前述,单旋转将 k 1 k1 k 1 k 2 k2 k 2 k 2 k2 k 2 B B B k 1 k1 k 1 k 2 k2 k 2 C C C k 3 k3 k 3 k 2 k2 k 2 k 1 k1 k 1 k 3 k3 k 3 k 1 k1 k 1 k 3 k3 k 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 private AvlNode<E> rotateLeftRight (AvlNode<E> k3) { k3.left = rotateLeft(k3.left); return rotateRight(k3); }
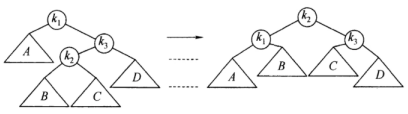
右-左双旋转(情形3): 如下图左侧的树,在 k 1 k_1 k 1 k 3 k_3 k 3 k 1 k_1 k 1 k 1 k_1 k 1
恢复平衡的旋转操作与左右双旋转类似,以下给出右左双旋转的代码实现。
1 2 3 4 private AvlNode<E> rotateRightLeft (AvlNode<E> k1) { k1.right = rotateRight(k1.right); return rotateLeft(k1); }
AVL树类架构
以下是AVL查找树类 AvlTree 的架构。
类成员/方法
描述
private AvlNode<E> root字段,AVL树的根结点
private static final int ALLOWED_IMBALANCE = 1常量字段,结点的失衡判定值,大于此值则失衡
public AvlTree()无参构造器,r o o t root roo t n u l l null n u ll
public void makeEmpty()树置空
public boolean isEmpty()判断树是否为空
public void insert(E e)插入结点驱动方法
public void remove(E e)删除结点驱动方法
public E findMin()查找最小结点驱动方法
public E findMax()查找最大结点驱动方法
public boolean contains(E e)判断是否包含指定元素驱动方法
public void printTree()按中序遍历打印树的驱动方法
public int size()求树的结点个数驱动方法
public int height()求树的高度驱动方法
public void checkBalance()树平衡检查驱动方法
private AvlNode<E> balance(AvlNode<E> t)调整 t t t t t t t t t t t t r o t a t e R i g h t rotateRight ro t a t e R i g h t t t t r o t a t e L e f t R i g h t rotateLeftRight ro t a t e L e f tR i g h t t t t r o t a t e L e f t rotateLeft ro t a t e L e f t t t t r o t a t e R i g h t L e f t rotateRightLeft ro t a t e R i g h t L e f t
private AvlNode<E> insert(E e, AvlNode<E> t)插入结点b a l a n c e ( t ) balance(t) ba l an ce ( t ) t t t t t t t t t
private AvlNode<E> remove(E e, AvlNode<E> t)删除结点(懒惰删除)b a l a n c e ( t ) balance(t) ba l an ce ( t ) t t t t t t t t t t t t
private AvlNode<E> findMin(AvlNode<E> t)返回树的最小结点
private AvlNode<E> findMax(AvlNode<E> t)返回树的最大结点
private boolean contains(E e, AvlNode<E> t)判断树中是否有指定元素的结点
private void printTree(AvlNode<E> t)中序遍历打印树
private int height(AvlNode<E> t)返回以 t t t
private int size(AvlNode<E> t)递归地遍历所有结点,返回结点总数
private int checkBalance(AvlNode<E> t)检查树是否平衡,不平衡打印“imbalance”,并返回树高度
private AvlNode<E> rotateRight(AvlNode<E> k2)右单旋转
private AvlNode<E> rotateLeft(AvlNode<E> k1)左单旋转
private AvlNode<E> rotateLeftRight(AvlNode<E> k3)左右双旋转
private AvlNode<E> rotateRightLeft(AvlNode<E> k1)右左双旋转
以下为 AVL 树结点嵌套类 A v l N o d e AvlNode A v lN o d e
类成员/方法
描述
public E element字段,本结点元素
public AvlNode<E> left字段,本结点的左子结点
public AvlNode<E> right字段,本结点的右子结点
public int height字段,该结点的高度
public AvlNode(E theElement)构造器
public AvlNode(E element, AvlNode<E> left, AvlNode<E> right)构造器
主要方法
insert
插入结点操作由插入驱动方法和具体插入方法完成,与 BST 的插入方法的不同在于,插入后通过 b a l a n c e balance ba l an ce t t t b a l a n c e balance ba l an ce 插入路径上所有结点的平衡 ,且实际上在调整 第一个 (自底向上方向上的第一个)失衡结点后使整棵树恢复为 AVL 树。b a l a n c e balance ba l an ce
1 2 3 4 5 6 7 8 9 10 11 public void insert (E e) { root = insert(e, root); } private AvlNode<E> insert (E e, AvlNode<E> t) { if (t == null ) return new AvlNode <>(e,null , null ); int compareRes = e.compareTo(t.element); if (compareRes < 0 ) t.left = insert(e, t.left); else if (compareRes > 0 ) t.right = insert(e, t.right); return balance(t); }
findMin/findMax
与 BST 的对应方法一致。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public E findMin () { if (isEmpty()) throw new NoSuchElementException (); return findMin(root).element; } private AvlNode<E> findMin (AvlNode<E> t) { if (t == null ) return null ; else if (t.left == null ) return t; return findMin(t.left); } public E findMax () { if (isEmpty()) throw new NoSuchElementException (); return findMax(root).element; } private AvlNode<E> findMax (AvlNode<E> t) { if (t == null ) return null ; while (t.right != null ) t = t.right; return t; }
remove
删除结点操作由删除驱动方法和具体删除方法完成,与 BST 的删除方法的不同在于,删除后通过 b a l a n c e balance ba l an ce t t t b a l a n c e balance ba l an ce 插入路径上所有结点的平衡 ,且实际上在调整 第一个 (自底向上方向上的第一个)失衡结点后使整棵树恢复为 AVL 树。b a l a n c e balance ba l an ce
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public void remove (E e) { root = remove(e, root); } private AvlNode<E> remove (E e, AvlNode<E> t) { if (t == null ) return null ; int compareRes = e.compareTo(t.element); if (compareRes < 0 ) t.left = remove(e, t.left); else if (compareRes > 0 ) t.right = remove(e, t.right); else if (t.left != null && t.right != null ) { t.element = findMin(t.right).element; t.right = remove(t.element, t.right); } else t = (t.left != null ) ? t.left : t.right; return balance(t); }
contains
与 BST 的对应方法一致。
1 2 3 4 5 6 7 8 9 10 public boolean contains (E e) { return contains(e, root); } private boolean contains (E e, AvlNode<E> t) { if (t == null ) return false ; int compareRes = e.compareTo(t.element); if (compareRes < 0 ) return contains(e, t.left); else if (compareRes > 0 ) return contains(e, t.right); else return true ; }
balance
在每一次插入或删除结点后,路径上结点 t t t t t t ALLOWED_IMBALANCE = 1),若超过则分别判断属于左-左、左-右、右-右、右-左中的哪一种情形,调用相应的旋转方法调整即可。该方法返回 t t t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 private AvlNode<E> balance (AvlNode<E> t) { if (t == null ) return null ; if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) { if (height(t.left.left) >= height(t.left.right)){ t = rotateRight(t); } else t = rotateLeftRight(t); } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE){ if (height(t.right.right) >= height(t.right.left)) { t = rotateLeft(t); } else t = rotateRightLeft(t); } t.height = Math.max(height(t.left), height(t.right)) + 1 ; return t; }
rotateRight
右单旋转,见前述说明。
rotateLeft
左单旋转,见前述说明。
rotateLeftRight
左右双旋转,见前述说明。
rotateRightLeft
右左双旋转,见前述说明。
checkBalance
检查整棵树是否平衡的方法。由平衡检查驱动方法和具体平衡检查方法完成。具体方法中以递归方式检查,若平衡则返回树高,不平衡则打印 i m b a l a n c e imbalance imba l an ce
1 2 3 4 5 6 7 8 9 10 11 12 13 public void checkBalance () { checkBalance(root); } private int checkBalance (AvlNode<E> t) { if (t == null ) return -1 ; int lh = checkBalance(t.left); int rh = checkBalance(t.right); if (Math.abs(height(t.left) - height(t.right)) > 1 || height(t.left) != lh || height(t.right) != rh) { System.out.println("imbalance" ); } return height(t); }
类的实现代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 class AvlTree <E extends Comparable <? super E>>{ private AvlNode<E> root; private static final int ALLOWED_IMBALANCE = 1 ; public AvlTree () {} public void makeEmpty () { root = null ; } public boolean isEmpty () { return root == null ; } public void insert (E e) { root = insert(e, root); } public void remove (E e) { root = remove(e, root); } public E findMin () { if (isEmpty()) throw new NoSuchElementException (); return findMin(root).element; } public E findMax () { if (isEmpty()) throw new NoSuchElementException (); return findMax(root).element; } public boolean contains (E e) { return contains(e, root); } public void printTree () { if (isEmpty()) System.out.println("Empty tree" ); else printTree(root); } public int size () { return size(root); } public int height () { return height(root); } public void checkBalance () { checkBalance(root); } private AvlNode<E> balance (AvlNode<E> t) { if (t == null ) return null ; if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) { if (height(t.left.left) >= height(t.left.right)){ t = rotateRight(t); } else t = rotateLeftRight(t); } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE){ if (height(t.right.right) >= height(t.right.left)) { t = rotateLeft(t); } else t = rotateRightLeft(t); } t.height = Math.max(height(t.left), height(t.right)) + 1 ; return t; } private AvlNode<E> insert (E e, AvlNode<E> t) { if (t == null ) return new AvlNode <>(e,null , null ); int compareRes = e.compareTo(t.element); if (compareRes < 0 ) t.left = insert(e, t.left); else if (compareRes > 0 ) t.right = insert(e, t.right); return balance(t); } private AvlNode<E> remove (E e, AvlNode<E> t) { if (t == null ) return null ; int compareRes = e.compareTo(t.element); if (compareRes < 0 ) t.left = remove(e, t.left); else if (compareRes > 0 ) t.right = remove(e, t.right); else if (t.left != null && t.right != null ) { t.element = findMin(t.right).element; t.right = remove(t.element, t.right); } else t = (t.left != null ) ? t.left : t.right; return balance(t); } private AvlNode<E> findMin (AvlNode<E> t) { if (t == null ) return null ; else if (t.left == null ) return t; return findMin(t.left); } private AvlNode<E> findMax (AvlNode<E> t) { if (t == null ) return null ; while (t.right != null ) t = t.right; return t; } private boolean contains (E e, AvlNode<E> t) { if (t == null ) return false ; int compareRes = e.compareTo(t.element); if (compareRes < 0 ) return contains(e, t.left); else if (compareRes > 0 ) return contains(e, t.right); else return true ; } private void printTree (AvlNode<E> t) { if (t != null ) { printTree(t.left); System.out.println(t.element); printTree(t.right); } } private int height (AvlNode<E> t) { return t == null ? -1 : t.height; } private int size (AvlNode<E> t) { if (t != null ) { if (t.left != null && t.right != null ) { return 1 + size(t.left) + size(t.right); } else { return t.left != null ? 1 + size(t.left) : 1 + size(t.right); } } return 0 ; } private int checkBalance (AvlNode<E> t) { if (t == null ) return -1 ; int lh = checkBalance(t.left); int rh = checkBalance(t.right); if (Math.abs(height(t.left) - height(t.right)) > 1 || height(t.left) != lh || height(t.right) != rh) { System.out.println("imbalance" ); } return height(t); } private AvlNode<E> rotateRight (AvlNode<E> k2) { AvlNode<E> k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; k1.height = Math.max(height(k1.left), height(k1.right)) + 1 ; return k1; } private AvlNode<E> rotateLeft (AvlNode<E> k1) { AvlNode<E> k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = Math.max(height(k1.left), height(k1.right)) + 1 ; k2.height = Math.max(height(k2.left), height(k2.right)) + 1 ; return k2; } private AvlNode<E> rotateLeftRight (AvlNode<E> k3) { k3.left = rotateLeft(k3.left); return rotateRight(k3); } private AvlNode<E> rotateRightLeft (AvlNode<E> k1) { k1.right = rotateRight(k1.right); return rotateLeft(k1); } private static class AvlNode <E>{ public E element; public AvlNode<E> left, right; public int height; @SuppressWarnings("unused") public AvlNode (E theElement) { this (theElement, null , null ); } public AvlNode (E element, AvlNode<E> left, AvlNode<E> right) { this .element = element; this .left = left; this .right = right; this .height = 0 ; } } }
测试代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 package com.yukiyama;import java.util.NoSuchElementException;public class AvlTreeDemo { public static void main (String[] args) { AvlTree<Integer> t = new AvlTree <>( ); int [] elements = {3 ,2 ,1 ,4 ,5 ,6 ,7 ,16 ,15 ,14 ,13 ,12 ,11 ,10 ,8 ,9 }; for (int e : elements) t.insert(e); t.printTree(); System.out.printf("size: %d, height: %d, min: %d, max: %d\n" , t.size(), t.height(), t.findMin(), t.findMax()); System.out.printf("has 10? %s, has 100? %s\n" , t.contains(10 ), t.contains(100 )); t.checkBalance(); t.remove(1 ); t.checkBalance(); t.remove(10 ); t.checkBalance(); t.remove(16 ); t.checkBalance(); t.printTree(); System.out.printf("size: %d, height: %d\n" , t.size(), t.height()); System.out.println("is empty: " + t.isEmpty()); t.makeEmpty(); System.out.println("is empty: " + t.isEmpty()); } }