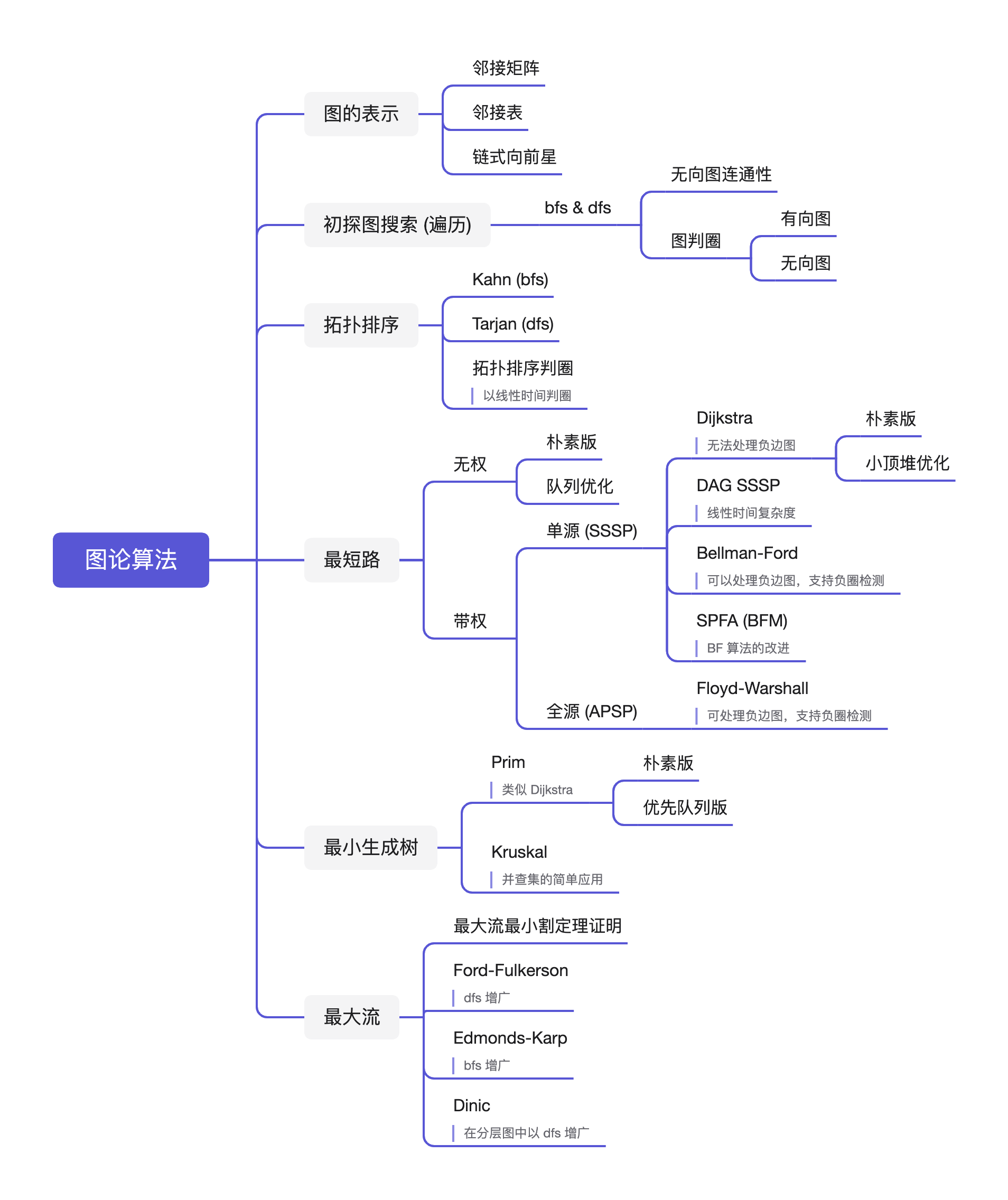
图论算法,拿得起放得下
可在作者的 github仓库 中获取本文和其他文章的 markdown 源文件及相关代码。
欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题,我将长期维护所有文章。
所有文章均用 Typora 完成写作,可使用 Typora 打开文章 md 文件,以获得最佳阅读体验。
⚠️ ⚠️ ⚠️ 本文巨巨巨长,正文近六万字 (不含题解),尽最大努力全面细致地讲解 bfs/dfs、拓扑排序、最短路、最小生成树、最大流,包括不仅限于给出每个专题内容的不同的常见算法 (如在最短路会讲解 DAG SSSP, Dijkstra, Bellman-Ford, SPFA, Floyd-Warshall 等算法),每一个算法的每一步操作的细节、算法正确性证明、复杂度证明以及完整的可应用的实现代码。全面、细致、系统、准确是本文的追求。
❗️ 【NEW】 ❗️
k e y w o r d s keywords k ey w or d s
图的基本概念 / 邻接矩阵 / 邻接表 / 链式向前星 / b f s bfs b f s d f s dfs df s K a h n Kahn K ahn T a r j a n Tarjan T a r jan D i j k s t r a Dijkstra D ijk s t r a B e l l m a n − F o r d Bellman-Ford B e ll man − F or d S P F A SPFA SPF A F l o y d − W a r s h a l l Floyd-Warshall Fl oy d − Wa rs ha ll P r i m Prim P r im K r u s k a l Kruskal Kr u s ka l F o r d − F u l k e r s o n Ford-Fulkerson F or d − F u l k erso n E d m o n d s − K a r p Edmonds-Karp E d m o n d s − K a r p D i n i c Dinic D ini c
这是 yuki 最近一段时间学习图论的总结,发出来跟大家分享 亿点点 🤏心得。写这篇文章的契机是前段时间看 Weiss 那本 「数算Java描述」,看着看着发现到图论那章作者就只提供伪代码了 (之前的章节会提供完整的可运行代码),而且感觉 Weiss 在那一章里什么都提一点,但匆匆抛出几个结论就跑路,整章看下来比较难受。找了好多资料,包括力扣上几本相关的 leetbook,都不太满意。于是乎花了点时间探索整理了一下,写成本文,(我认为的) 优点有四。
面向小白,入门友好 。主要针对像我一样的初学者,或者粗浅地看过一些图论算法,但感觉不是特别踏实的朋友。这里的「不踏实」指的是在题解区看到一个问题有眼花缭乱的多种图论方法,但自己只知道常用的那种,有的压根没听过;也可以指的是虽然知道怎么做,但相关算法的正确性证明或复杂度证明,未曾确切地把握过。循序渐进,反馈及时 。特别突出了各章节之间的联系与过渡。为了使读者能够在每一章学习中都有及时的正反馈,每介绍一个算法,我都会配套一道力扣上的原题 (力扣没有典型题目则采用其他平台的题目)。编排得当,重点全面。 内容编排上作者也颇费苦心,例如「初探图搜索 (遍历)」一节,推敲几日,最终决定用「无向图连通性」问题引入 b f s / d f s bfs/dfs b f s / df s b f s / d f s bfs/dfs b f s / df s b f s / d f s bfs/dfs b f s / df s 证明翔实,有根有据 。在「最短路」和「最大流」这两个章节中,对所有不易看出的结论均给出了详细的,较为严格的证明。包括且不限于对 Dijkstra、Prim、Bellman-Ford、SPFA、Floyd-Warshall 算法的正确性证明,对「最大流最小割定理」的证明,对 Edmonds-Karp、Dinic 算法复杂度的证明等。 部分证明着实耗尽了作者的最后一点智商,导致目前 智商欠费,大脑停机 。
本文所涉具已呈于「主要内容一览」中,如果朋友们觉得合适,不妨一看。希望朋友们能感受到 yuki 的 亿点用心 。
本文标题 意在表达作者的一种「希望」,即通过本文的学习,看似沉重的图论算法,也能 重重拿起,轻轻放下 。
然而不幸的是,作者能力水平十分有限,文章虽已审视几轮,所列代码也悉经验证,但根据之前几篇文章的经验,这一篇也会毫无例外地出现一些错误。因此本文既是心得分享,也是小白 yuki 再次向大家请教的一次机会,文中若有疏漏之处,请各位不吝赐教 🤝。
※ Dinic 的代码还需一些时间验证,暂不列出。「实战应用」中目前有十几题,会持续增加,整篇文章也会持续维护。
※ 部分算法正确性证明及复杂度证明以单篇文章发布过,但为了保持本文完整度,也一并呈现。
※ 内容可能较多,可根据目录选择性阅读。
yuki的其他文章如下,欢迎阅读指正!
如下所有文章同时也在我的 github 仓库 中维护。
[2022-12-01]
[2022-09-28]
概览
内容一览
图论算法复杂度一览
以下列出本文讲解的全部图论算法的时空复杂度。
分类
算法
时间复杂度
图遍历
bfs
O ( V + E ) O(V+E) O ( V + E )
dfs
O ( V + E ) O(V+E) O ( V + E )
拓扑排序
Kahn
O ( V + E ) O(V+E) O ( V + E )
Tarjan (TopoSort)
O ( V + E ) O(V+E) O ( V + E )
最短路
无权SSSP 朴素版
O ( V 2 ) O(V^2) O ( V 2 )
无权SSSP 队列版
O ( V + E ) O(V+E) O ( V + E )
Dijkstra 朴素版
O ( V 2 ) O(V^2) O ( V 2 )
Dijkstra 优先队列版
O ( E l o g V ) O(ElogV) O ( El o g V )
DAG SSSP
O ( V + E ) O(V+E) O ( V + E )
Bellman-Ford
O ( V E ) O(VE) O ( V E )
SPFA (BFM)
O ( V E ) O(VE) O ( V E )
Floyd-Warshall
O ( V 3 ) O(V^3) O ( V 3 )
最小生成树
Prim 朴素版
O ( V 2 ) O(V^2) O ( V 2 )
Prim 优先队列版
O ( E l o g V ) O(ElogV) O ( El o g V )
Kruskal
O ( E l o g V ) O(ElogV) O ( El o g V )
最大流
Ford-Fulkerson
O ( E ∗ f ) O(E*f) O ( E ∗ f )
Edmonds-Karp
O ( V E 2 ) O(VE^2) O ( V E 2 )
Dinic (Dinitz)
O ( V 2 E ) O(V^2E) O ( V 2 E )
※ V V V E E E V V V E E E ∣ V ∣ |V| ∣ V ∣ ∣ E ∣ |E| ∣ E ∣
※ 空间复杂度主要取决于建图方式,以「邻接矩阵」建图时为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
图的基本概念
概念
描述
顶点 & 边vertex & edge
一对顶点 ( u , v ) , u , v ∈ V (u, v), u, v ∈ V ( u , v ) , u , v ∈ V V V V E E E E E E V V V
图graph
顶点集 V V V E E E
权 / 值weight / cost
边的权重。
邻接adjacent
顶点 u u u v v v ( u , v ) ∈ E (u, v) ∈ E ( u , v ) ∈ E
邻接矩阵adjacent matrix
以矩阵表示图。对每条边 ( u , v ) (u, v) ( u , v ) A [ u , v ] A[u, v] A [ u , v ] t r u e true t r u e ( u , v ) (u, v) ( u , v ) f a l s e false f a l se A [ u , v ] A[u, v] A [ u , v ]
邻接表adjacency list
对每一个顶点,以一个表存放其邻接顶点,共以 V V V
无向图undirected graph
点无序的图,( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u )
有向图directed graph / digraph
点对有序的图,( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u )
度degree
对无向图顶点 v v v
入度indegree
对有向图顶点 v v v ( u , v ) (u, v) ( u , v )
出度outdegree
对有向图顶点 v v v ( v , u ) (v, u) ( v , u )
路径path
为一顶点序列 v 1 , v 2 , v 3 , . . . , v N v_1, v_2, v_3,...,v_N v 1 , v 2 , v 3 , ... , v N ( v i , v i + 1 ) ∈ E , 1 < = i < = N − 1 (v_i, v_{i+1}) ∈ E, 1<=i<=N-1 ( v i , v i + 1 ) ∈ E , 1 <= i <= N − 1
路径长度path length
无向图中指路径上的边数,有向图中指路径边权和。
简单路径simple path
所有顶点都不同的路径。
圈cycle
满足 v 1 = v N v_1 = v_N v 1 = v N
环 / 自环loop
一个顶点到它自身的边 ( v , v ) (v, v) ( v , v )
有向无环(圈)图directed acyclic graph, DAG
无(环)圈的有向图。
连通图connected graph
从一顶点 w w w v v v w w w v v v
连通分量connected component
对于无向图而言,一个极大连通子图为一个连通分量。
基础图underlying graph
有向图去掉边的方向后的图称为该有向图的基础图 (无向图)。
强连通strongly connected
称有向连通图是强连通的。
强连通分量strongly connected component (SCC)
对于有向图基础图的一个连通分量,
弱连通weakly connected
有向图不是强连通的,但其基础图是连通的,则称该有向图是弱连通的。
完全图complete graph
每一对顶点间都有边相连的图。
在后续叙述中,我会假定你已熟悉该表所罗列概念。
图的表示
求解图上问题,首先要以合适的方式存储图。图的基本信息是顶点、边、边的方向以及边权,通过「邻接矩阵」或「邻接表」来存储图,可以很好地组织上述信息。本节简单介绍这两种存图方式,但暂不呈现相关代码,在后续章节解决实际问题时,我们会看到程序中是如何应用这两种方式存图以及提取图中的信息的。(本文大部分实现均采用「邻接表」法存图,若读者想立即参考「邻接矩阵」的具体写法,可参考「最短路径」-「带权全源最短路」-「Floyd-Warshall」-「代码」一节的代码。)
邻接矩阵
用二维数组 e d g e s [ ] [ ] edges[][] e d g es [ ] [ ] ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 e d g e s [ u ] [ v ] edges[u][v] e d g es [ u ] [ v ] u u u v v v I n f i n i t y Infinity I n f ini t y O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
邻接表
对每一个顶点,以一个列表来存储其邻接顶点和相应的边权信息,于是图信息被存储在 ∣ V ∣ |V| ∣ V ∣ ∣ E ∣ |E| ∣ E ∣ O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 List<List<Integer>> graph 存图,通过 graph.get(u).get(v) 来获取边 ( u , v ) (u, v) ( u , v ) i n t [ ] int[] in t [ ] List<List<int[]>> graph 存图,对于 int[] v_weight = graph.get(u) ,v _ w e i g h t v\_weight v _ w e i g h t v _ w e i g h t [ 0 ] v\_weight[0] v _ w e i g h t [ 0 ] u u u v v v v _ w e i g h t [ 1 ] v\_weight[1] v _ w e i g h t [ 1 ] ∣ ( u , v ) ∣ |(u,v)| ∣ ( u , v ) ∣ List<List<Pair>> graph 存图,但本文不采用此种写法。
当顶点不适合用非负整数表示时,例如为字符串或其他引用类型,则可用哈希表存图,k e y ke y k ey v a l u e value v a l u e k e y key k ey
链式向前星
相比前两种存图法,「链式向前星」存图法是一种极具技巧性的存图方式,虽不太直观,但有不少优点,我们先来介绍其具体实现,再分析其优点。
首先,链式向前星的 本质也是「邻接表」 ,与邻接表法的显式邻接表 (即 g r a p h . g e t ( u ) graph.get(u) g r a p h . g e t ( u ) u u u L i s t List L i s t 「边下标指针」 来获取一个顶点的邻边信息。我们直接给出链式向前星具体的存图结构,然后再描述如何通过这样的安排来存图,使得我们能够获取图的相关信息,例如遍历一个顶点的所有边 (邻接顶点) 。
边从 1 1 1 ∣ E ∣ |E| ∣ E ∣
e n d s [ ] ends[] e n d s [ ] ∣ E ∣ + 1 |E|+1 ∣ E ∣ + 1 e n d s [ e d g e N u m ] ends[edgeNum] e n d s [ e d g e N u m ] e d g e N u m edgeNum e d g e N u m
w e i g h t s [ ] weights[] w e i g h t s [ ] ∣ E ∣ + 1 |E|+1 ∣ E ∣ + 1 w e i g h t s [ e d g e N u m ] weights[edgeNum] w e i g h t s [ e d g e N u m ] e d g e N u m edgeNum e d g e N u m
n e x t s [ ] nexts[] n e x t s [ ] ∣ E ∣ + 1 |E|+1 ∣ E ∣ + 1 u u u n e x t s [ e d g e N u m ] nexts[edgeNum] n e x t s [ e d g e N u m ] e d g e N u m edgeNum e d g e N u m 「在其所在的顶点邻接表」 中的下一条边。
h e a d s [ ] heads[] h e a d s [ ] ∣ V ∣ |V| ∣ V ∣ u u u h e a d s [ u ] heads[u] h e a d s [ u ] u u u
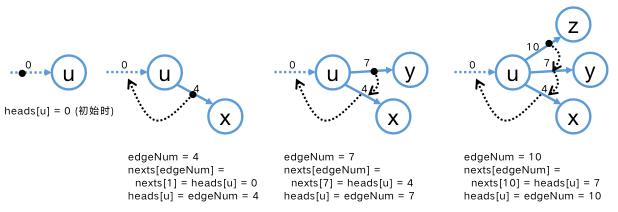
链式向前星通过「插头法」加边建图,伪代码如下,建议结合后图分析此伪代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int n, m, edgeNum int [] heads = new int [n]int [] weights = new int [m + 1 ], ends = new int [m + 1 ], nexts = new int [m + 1 ]int u, v, weight ++edgeNum weights[edgeNum] = weight ends[edgeNum] = v nexts[edgeNum] = heads[u] heads[u] = edgeNum
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int n, m, edgeNum int [] heads = new int [n]int [] ends = new int [2 * m + 1 ], nexts = new int [2 * m + 1 ]int u, v, val ++edgeNum ends[edgeNum] = v nexts[edgeNum] = heads[u] heads[u] = edgeNum ++edgeNum ends[edgeNum] = u nexts[edgeNum] = heads[v] heads[v] = edgeNum
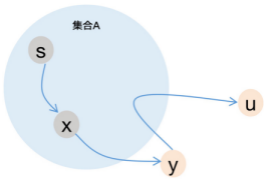
通过下图展示顶点 u u u e d g e N u m , h e a d s , n e x t s edgeNum, heads, nexts e d g e N u m , h e a d s , n e x t s u u u h e a d s [ u ] heads[u] h e a d s [ u ]
在遍历边建图之前,heads[u] = 0 ,表示此时 u u u
在遍历到第 4 条边时 (前三条边与 u u u u u u u u u ( u , x ) (u,x) ( u , x ) e d g e N u m = 4 edgeNum = 4 e d g e N u m = 4 h e a d s [ u ] = 4 heads[u] = 4 h e a d s [ u ] = 4 n e x t s [ 4 ] = 0 nexts[4] = 0 n e x t s [ 4 ] = 0
1 2 3 int tmp = heads[u]; heads[u] = edgeNum; nexts[edgeNum] = tmp;
实际上我们可以先设置 n e x t s [ e d g e N u m ] nexts[edgeNum] n e x t s [ e d g e N u m ] h e a d s [ u ] heads[u] h e a d s [ u ] t m p tmp t m p
1 2 nexts[edgeNum] = heads[u]; heads[u] = edgeNum;
继续遍历边建图,我们在遍历到第 7 条边时遇到第二条 u u u ( u , y ) (u,y) ( u , y ) u u u ( u , z ) (u,z) ( u , z )
从上述伪代码和图示中我们感到 nexts[edgeNum] = heads[u] 较难理解,此行是体现链式向前星「插头法」的核心,建图过程中我们总是以 h e a d s [ u ] heads[u] h e a d s [ u ] u u u u u u e d g e N u m = h e a d s [ u ] edgeNum = heads[u] e d g e N u m = h e a d s [ u ] u u u e d g e N u m = n e x t s [ e d g e N u m ] edgeNum = nexts[edgeNum] e d g e N u m = n e x t s [ e d g e N u m ] u u u e d g e N u m = n e x t s [ e d g e N u m ] = 0 edgeNum = nexts[edgeNum] = 0 e d g e N u m = n e x t s [ e d g e N u m ] = 0 u u u
1 2 3 4 for (int edgeNum = heads[u]; edgeNum != 0 ; edgeNum = nexts[edgeNum]){ int v = ends[edgeNum]; int weight = weights[edgeNum]; }
如果还是不太好理解,我们可以把 e d g e edge e d g e E d g e Edge E d g e n e x t s [ e d g e N u m ] nexts[edgeNum] n e x t s [ e d g e N u m ] e d g e . n e x t edge.next e d g e . n e x t h e a d E d g e headEdge h e a d E d g e u u u h e a d [ u ] head[u] h e a d [ u ] u . h e a d E d g e u.headEdge u . h e a d E d g e
1 2 3 4 5 6 遍历到 u 的新边 edge 后的「插头」操作 edge.next = u.headEdge; u.headEdge = edge; 遍历 u 的边 for (Edge edge = u.headEdge; edge != null ; edge = edge.next)
现在我们能够看出「链式向前星」的如下优点:
空间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) L i s t List L i s t
由于存粹以数组存图,因此处理速度也会比 L i s t List L i s t
由于对边编号,在某些需要处理一条边的反向边的场景下 (例如最大流算法中),可以很方便地操作反向边 (具体看「小结」)。
读者若想尽快把握该存图操作,可直接查看如下位置的相应代码。
无权无向图: 「初探图搜索 (遍历)」-「无向图连通性」-「BFS」-「代码」
带权有向图: 「最短路径」-「带权单源最短路」-「Dijkstra」-「优先队列版」-「代码」
※ 从前面的图示可以看出「链式向前星」这个命名是很贴切的。根据知乎问题 链式前向星的发明者是谁? ,知乎用户「Malash」似乎是中文「链式向前星」一词的命名者。根据该问题下 「Yixiao Huang」 用户的回答,该存图方式似乎出自此篇发表于 1987 年的论文 A versatile data structure for edge-oriented graph algorithms 。
小结
本节学习了三种图的表示方法,各有特点,也有各自适合的应用场景。
对已知「稠密图」建图,或需要频繁地根据两个顶点来读写边权的场景时,考虑「邻接矩阵」。
对已知「稀疏图」建图,或只需根据顶点 u u u
在希望空间复杂度更优,又需要操作「反向边」的场景,考虑「链式向前星」。
操作
邻接矩阵
邻接表
链式向前星
编写
容易
容易
相对复杂
空间
O ( V 2 ) O(V^2) O ( V 2 ) O ( V + E ) O(V+E) O ( V + E ) O ( V + E ) O(V+E) O ( V + E )
遍历 u u u
遍历 d i s t s [ u ] dists[u] d i s t s [ u ] O ( V ) O(V) O ( V )
遍历 g r a p h . g e t ( u ) graph.get(u) g r a p h . g e t ( u ) O ( V ) O(V) O ( V )
e d g e N u m = h e a d s [ u ] edgeNum = heads[u] e d g e N u m = h e a d s [ u ] e d g e N u m = n e x t s [ e d g e N u m ] edgeNum = nexts[edgeNum] e d g e N u m = n e x t s [ e d g e N u m ] O ( V ) O(V) O ( V )
根据 u , v u, v u , v ( u , v ) (u,v) ( u , v )
d i s t s [ u ] [ v ] dists[u][v] d i s t s [ u ] [ v ] O ( 1 ) O(1) O ( 1 ) 遍历 g r a p h . g e t ( u ) graph.get(u) g r a p h . g e t ( u ) O ( V ) O(V) O ( V )
e d g e N u m = h e a d s [ u ] edgeNum = heads[u] e d g e N u m = h e a d s [ u ] e d g e N u m = n e x t s [ e d g e N u m ] edgeNum = nexts[edgeNum] e d g e N u m = n e x t s [ e d g e N u m ] O ( V ) O(V) O ( V )
根据 ( u , v ) (u,v) ( u , v ) ( v , u ) (v,u) ( v , u )
d i s t s [ v ] [ u ] dists[v][u] d i s t s [ v ] [ u ] O ( 1 ) O(1) O ( 1 ) 遍历 g r a p h . g e t ( v ) graph.get(v) g r a p h . g e t ( v ) O ( V ) O(V) O ( V )
若已知 ( u , v ) (u,v) ( u , v ) k ,[ 2 , E + 1 ] , [2,E+1] , [ 2 , E + 1 ] , ( v , u ) (v, u) ( v , u ) k^1 O ( 1 ) O(1) O ( 1 )
※ 链式向前星取反向边操作的说明:
将边编号为 [ 2 , E + 1 ] [2,E+1] [ 2 , E + 1 ] [ 0 , E − 1 ] [0, E-1] [ 0 , E − 1 ] k k k ( u , v ) (u,v) ( u , v ) k + 1 k+1 k + 1 ( v , u ) (v, u) ( v , u )
所有编号为偶数的边,若记作 k k k k + 1 k+1 k + 1
所有编号为奇数的边,若记作 k k k k − 1 k-1 k − 1
上述两种情况可统一为 k^1 ,^ 为异或运算。
另外,并非所有图论问题都需要「建图」,因为问题的输入本身就包含了图的信息,只不过通常需要组织成适合算法操作的结构,若该输入可直接被算法操作,也就不必再另外「建图」了。例如在「最小生成树」-「Kruskal」一节中,利用输入 c o n n e c t i o n s connections co nn ec t i o n s
初探图搜索 (遍历)
图的搜索 (s e a r c h search se a rc h t r a v e r s a l traversal t r a v ers a l 「搜索」 一词的重点在于关注图中的一个 t a r g e t target t a r g e t 「遍历」 一词的重点在于对整张图无遗漏地探索,多数时候这两个词是通用的。如同「树」的 深度优先搜索 (d f s dfs df s 广度优先搜索 (b f s bfs b f s
b f s bfs b f s d f s dfs df s 基本写法 ,就足以支撑我们学习后续更高级的图论算法。为了能够在学习中及时得到反馈,本节以如下三道基本题目引入并详细介绍最基本的 b f s bfs b f s d f s dfs df s
※ 当讨论「连通性」时,通常是对「无向图」而言的,即不关注边方向,只关注那些通过边互相连通的连通分量。在「有向图」中,另有「强连通分量」概念,我们已在「基本概念」中给出定义。
※ 这三道题均有适用性更强的「并查集」解法。如果你尚未学习过「并查集」或仍觉得不太熟练,可以参考我写的 并查集从入门到出门 ,全文 1w+ 字,尝试透彻分析并查集的基本内容,2022年5月中旬在力扣讨论区发布后半个月内收获 5k 阅读量,500+ 收藏,100+ 点赞。
无向图连通性
首先通过考察「无向图连通性」问题 323. 无向图中连通分量的数目 来学习最基本的图的 b f s / d f s bfs / dfs b f s / df s
虽然此时我们还不知道要如何具体写出这两种算法的细节,但我们知道通过 b f s / d f s bfs / dfs b f s / df s u u u
依次访问所有顶点,对于当前顶点 u u u u u u
搜索过程中,跳过那些「已访问」的顶点,对于「未访问」的顶点,显然它们与 u u u
因为从 u u u u u u
上述过程的实现需要设置一个 b o o l e a n boolean b oo l e an v i s i t e d visited v i s i t e d b f s bfs b f s d f s dfs df s
※ 通过 b f s / d f s bfs / dfs b f s / df s 逐渐标记整张图 (的所有顶点) 的做法,也被形象地称之为 flood fill (泛洪) 「记忆化搜索」 的应用。
※ 若采用 b f s bfs b f s
BFS
采用 b f s bfs b f s b f s bfs b f s u u u u u u u u u v v v 按层 完成所有与 u u u 双向建边 。
一般可用哈希表 M a p < k , v > Map<k, v> M a p < k , v > k k k v v v { 0 , 1 , 2 , . . . , n − 1 } \{0,1,2,...,n-1\} { 0 , 1 , 2 , ... , n − 1 } n n n List<List<Integer>> 存图效率更高,下标表示顶点,其对应的 List<Integer> 即为该顶点的邻接顶点表。通过下标可快速获取顶点的邻接表。
第一份代码以 哈希表 存图,适合于无法用连续的整数来表示顶点的场景。本题中,顶点可以被表示为 { 0 , 1 , 2 , 3 , . . . n − 1 } \{0, 1,2,3,...n - 1\} { 0 , 1 , 2 , 3 , ... n − 1 } 线性表 存图的代码效率更高。之后的内容,只要能够以线性表存图,就不再列出哈希表存图的版本。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution { public int countComponents (int n, int [][] edges) { Map<Integer, List<Integer>> graph = new HashMap <>(); for (int [] edge : edges){ int u = edge[0 ], v = edge[1 ]; List<Integer> uAdj = graph.getOrDefault(u, new ArrayList <>()); uAdj.add(v); graph.put(u, uAdj); List<Integer> vAdj = graph.getOrDefault(v, new ArrayList <>()); vAdj.add(u); graph.put(v, vAdj); } boolean [] visited = new boolean [n]; int count = 0 ; for (int u = 0 ; u < n; ++u){ if (!visited[u]){ count++; bfs(u, visited, graph); } } return count; } public void bfs (int u, boolean [] visited, Map<Integer, List<Integer>> graph) { Queue<Integer> q = new ArrayDeque <>(); q.add(u); while (!q.isEmpty()){ u = q.remove(); visited[u] = true ; List<Integer> uAdj = graph.get(u); if (uAdj != null ){ for (int v : graph.get(u)){ if (!visited[v]) q.add(v); } } } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution { public int countComponents (int n, int [][] edges) { List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < n; ++i) graph.add(new ArrayList <>()); for (int [] edge : edges){ int u = edge[0 ], v = edge[1 ]; graph.get(u).add(v); graph.get(v).add(u); } boolean [] visited = new boolean [n]; int count = 0 ; for (int u = 0 ; u < n; ++u){ if (!visited[u]){ count++; bfs(u, visited, graph); } } return count; } public void bfs (int u, boolean [] visited, List<List<Integer>> graph) { Queue<Integer> q = new ArrayDeque <>(); q.add(u); while (!q.isEmpty()){ u = q.remove(); visited[u] = true ; for (int v : graph.get(u)){ if (!visited[v]) q.add(v); } } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution { public int countComponents (int n, int [][] edges) { List<List<Integer>> graph = new ArrayList <>(); int m = edges.length, edgeNum = 0 ; int [] ends = new int [2 * m + 1 ], nexts = new int [2 * m + 1 ]; int [] heads = new int [n]; boolean [] visited = new boolean [n]; for (int [] edge : edges){ int u = edge[0 ], v = edge[1 ]; ++edgeNum; ends[edgeNum] = v; nexts[edgeNum] = heads[u]; heads[u] = edgeNum; ++edgeNum; ends[edgeNum] = u; nexts[edgeNum] = heads[v]; heads[v] = edgeNum; } int count = 0 ; for (int u = 0 ; u < n; u++){ if (!visited[u]) { count++; bfs(u, visited, heads, ends, nexts); } } return count; } private void bfs (int u, boolean [] visited, int [] heads, int [] ends, int [] nexts) { Queue<Integer> q = new ArrayDeque <>(); q.add(u); visited[u] = true ; while (!q.isEmpty()){ int v = q.remove(); for (int edgeNum = heads[v]; edgeNum != 0 ; edgeNum = nexts[edgeNum]) { int w = ends[edgeNum]; if (!visited[w]) { q.add(w); visited[w] = true ; } } } } }
这就是图的 最基本 的 b f s bfs b f s b f s bfs b f s
DFS
若搜索采用 d f s dfs df s u u u d f s dfs df s v i s i t e d [ u ] = t r u e visited[u] = true v i s i t e d [ u ] = t r u e f o r for f or d f s dfs df s d f s dfs df s u u u 必然 都被标记为「已访问」。代码如下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public int countComponents (int n, int [][] edges) { List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : edges){ int u = edge[0 ], v = edge[1 ]; graph.get(u).add(v); graph.get(v).add(u); } boolean [] visited = new boolean [n]; int count = 0 ; for (int u = 0 ; u < n; u++){ if (!visited[u]) { count++; dfs(u, visited, graph); } } return count; } private void dfs (int u, boolean [] visited, List<List<Integer>> graph) { visited[u] = true ; for (int v : graph.get(u)) { if (!visited[v]) dfs(v, visited, graph); } } }
这就是图的 最基本 的 d f s dfs df s d f s dfs df s
时空复杂度
时间复杂度:
无论是 b f s bfs b f s d f s dfs df s v v v v v v 完全图 (任意两个顶点间都有边连接),那么对第一个顶点 v v v ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d visited v i s i t e d O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) 线性空间复杂度 。
并查集
并查集是一种用来解决「连通分量」问题的专用性很强的数据结构,对于 323 题,最为直观合适且高效的办法是「并查集」。并查集本身也属「图论」范畴,我已经在另一篇文章中做过讲解,因此本文不再重复。作为图论的重要一环,并查集的学习是非常必要的,在后续「最小生成树」一节中,我们会再次看到它的身影。总之,如果你还不熟悉并查集,可以阅读我写的 并查集从入门到出门 (全文1w+字,尝试透彻分析并查集的基本内容,2022年5月中旬在力扣讨论区发布后半个月内收获 5k 阅读量,500+ 收藏,100+ 点赞) 。
判断图是否有圈
下面我们考察如何判断图是否有圈。以 684. 冗余连接 一题学习如何利用 b f s / d f s bfs / dfs b f s / df s 在无向图中判圈 ,以 207. 课程表 一题学习如何利用 b f s / d f s bfs / dfs b f s / df s 在有向图中判圈 。通过这两道题目,我们进一步加深对 b f s / d f s bfs / dfs b f s / df s
无向图判圈
对于 684. 冗余连接 ,题目要求我们找到使得图产生圈的 (在 e d g e s edges e d g es 最后出现的边 。有了上一节的经验,我们很容易想到,从某顶点 v v v b f s bfs b f s d f s dfs df s v v v v v v e d g e s edges e d g es 「加边法」 和 「减边法」 ,均为「泛洪法」。
加边法 & 减边法
加边法: 建图过程中,每加入一条边 ( u , v ) (u, v) ( u , v ) u u u v v v u u u v v v ( u , v ) (u, v) ( u , v ) e d g e s edges e d g es
减边法:加边法的逆过程。先完整建图,之后从 e d g e s edges e d g es ( u , v ) (u, v) ( u , v ) u u u v v v ( u , v ) (u, v) ( u , v )
这两种方法都很好理解,应用 b f s / d f s bfs / dfs b f s / df s 题解 。
比较此处的代码与「无向图连通性」一节的代码,可以看到基本框架一样,仅有以下不同,这些不同都是为适应本题所做的简单调整。
本题通过 b f s / d f s bfs/dfs b f s / df s
本题中,每次搜索结束后,若未找到圈,需要重置 v i s i t e d visited v i s i t e d
BFS 加边法代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int [] findRedundantConnection(int [][] edges) { int n = edges.length; boolean [] visited = new boolean [n]; List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < n; ++i) graph.add(new ArrayList <>()); for (int [] edge : edges){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 ; if (bfs(u, v, visited, graph)) { return new int []{u + 1 , v + 1 }; } graph.get(u).add(v); graph.get(v).add(u); Arrays.fill(visited, false ); } return null ; } public boolean bfs (int u, int v, boolean [] visited, List<List<Integer>> graph) { Queue<Integer> q = new ArrayDeque <>(); q.add(u); while (!q.isEmpty()){ u = q.remove(); visited[u] = true ; for (int w : graph.get(u)){ if (w == v) return true ; if (!visited[w]) q.add(w); } } return false ; } }
DFS 加边法代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { boolean hasCycle = false ; public int [] findRedundantConnection(int [][] edges) { int n = edges.length; boolean [] visited = new boolean [n]; List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < n; ++i) graph.add(new ArrayList <>()); for (int [] edge : edges){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 ; if (dfs(u, v, visited, graph)) { return new int []{u + 1 , v + 1 }; } graph.get(u).add(v); graph.get(v).add(u); Arrays.fill(visited, false ); } return null ; } public boolean dfs (int u, int v, boolean [] visited, List<List<Integer>> graph) { visited[u] = true ; for (int w : graph.get(u)){ if (w == v) hasCycle = true ; if (!visited[w]) hasCycle = dfs(w, v, visited, graph); } return hasCycle; } }
时空复杂度
时间复杂度: 最坏和平均时间复杂度都是 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d visited v i s i t e d O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
有向图判圈
684 题的图为无向图,现在我们通过 207. 课程表 一题来学习应用 b f s / d f s bfs / dfs b f s / df s 有向图中判圈 。
读题后不难看出课程之间的依赖关系可抽象成「图」。每一门课程为一个顶点,课程 v v v u u u ( u , v ) (u, v) ( u , v ) 当且仅当 这些课程构成的有向图 「无圈」 时,能够完成所有课程的学习。也就是我们只需要根据输入构建有向图,然后判断该图是否有圈即可,无圈返回 t r u e true t r u e f a l s e false f a l se
类似「无向图判圈」,我们同样可以用「加边法」或「减边法」来求解此题。差别仅在于如下几点。
本题为有向图,建图时只需单向建边。
考察边 ( u , v ) (u, v) ( u , v ) 单向性 ,应当以 v v v u u u
若存在自环,即 ( u , u ) (u, u) ( u , u ) t a r g e t target t a r g e t u u u
这些差别体现在代码中只有两三行的区别,有了之前的经验,我们能够轻松实现。应用 b f s / d f s bfs / dfs b f s / df s 题解 。
BFS 加边法代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public boolean canFinish (int numCourses, int [][] prerequisites) { List<List<Integer>> graph = new ArrayList <>(); boolean [] visited = new boolean [numCourses]; for (int i = 0 ; i < numCourses; ++i) { graph.add(new ArrayList <>()); } for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; if (u == v) return false ; if (bfs(v, u, visited, graph)) return false ; Arrays.fill(visited, false ); graph.get(u).add(v); } return true ; } private boolean bfs (int u, int target, boolean [] visited, List<List<Integer>> graph) { Queue<Integer> q = new ArrayDeque <>(); q.add(u); while (!q.isEmpty()){ u = q.remove(); visited[u] = true ; for (int v : graph.get(u)){ if (v == target) return true ; if (!visited[v]) q.add(v); } } return false ; } }
DFS 加边法代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { boolean hasCycle = false ; public boolean canFinish (int numCourses, int [][] prerequisites) { List<List<Integer>> graph = new ArrayList <>(); boolean [] visited = new boolean [numCourses]; for (int i = 0 ; i < numCourses; ++i) { graph.add(new ArrayList <>()); } for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; if (u == v) return false ; if (dfs(v, u, visited, graph)) return false ; Arrays.fill(visited, false ); graph.get(u).add(v); } return true ; } private boolean dfs (int u, int target, boolean [] visited, List<List<Integer>> graph) { visited[u] = true ; for (int v : graph.get(u)){ if (v == target) hasCycle = true ; if (!visited[v]) hasCycle = dfs(v, target, visited, graph); } return hasCycle; } }
时空复杂度
时间复杂度: 最坏和平均时间复杂度都是 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d visited v i s i t e d O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
小结
在本节中,我们通过「无向图的连通性」展示了图搜索 (遍历) 最基本的 b f s / d f s bfs / dfs b f s / df s 「无向图」和「有向图」 中如何应用节本的 b f s / d f s bfs / dfs b f s / df s
当我们重新审视「图判圈」问题时,我们会感觉到泛洪做法中有很多重复操作。我们每次加边前 (或减边后) 泛洪都是在当前整张图上进行的,我们自然会想,能否通过对原图的一次「遍历」来找到圈呢?答案是可以的,只需要在基本 b f s bfs b f s d f s dfs df s 「拓扑排序」 ,属于图论算法中比 b f s bfs b f s d f s dfs df s O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
现在你已经牢固掌握了图的 b f s bfs b f s d f s dfs df s
拓扑排序
拓扑排序 (Topological Sorting) : 对有向图的顶点的排序,如果存在从顶点 u u u v v v u u u v v v v v v u u u 有向图无圈 。且只要图为 D A G DAG D A G 至少存在一种拓扑排序结果 。此外,是否存在拓扑排序与图是否存在不连通的分量无关,这是显然的,因为互不连通的分量互不依赖,在拓扑排序中这些分量的顺序是任意的。
拓扑排序的主要实现为基于 B F S BFS BFS 「Kahn算法」 以及基于 D F S DFS D FS 「Tarjan拓扑排序算法」 。我们将看到,这两种算法实现的拓扑排序在求解过程上是 「互逆」 的。wiki 中对拓扑排序有如下 更准确的表述 ,后续我们会再次提到该「表述」。
Precisely, a topological sort is a graph traversal in which each node v v v
更准确地,拓扑排序是对图的一种遍历,在这种遍历中,对一个顶点 v v v
※ 大家思考过为什么这种排序要冠以「拓扑」之名吗?根据作者有限的了解,「拓扑学 (Topology)」研究的是平面或立体图形 (多维?) 连续变形过程中的性质。说一个什么事物是「拓扑的 (Topological)」似乎在表达这个事物变形前后的关系,看起来「拓扑排序」跟数学上的「拓扑」并没有什么关联,因为点或边或整张图并未有什么变化。查了一下,这篇讨论 Why is “topological sorting” topological? 的高赞回答表示该命名大概只是想体现 “network topology” 的味道 (sense)。
作者点评: 适当地探索一个技术名词的「语源」,能够加深我们对其的理解 🤔。
在前一节中,我们提到「图判圈」问题,也就是 684. 冗余连接 和 207. 课程表 两题可通过「拓扑排序」解决,且时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) 210. 课程表 II 一题为分析对象,该题目描述的内容常作为介绍拓扑排序的一个经典的现实例子 (具体看原题描述)。在本节最后再给出 684 和 207 题的「拓扑排序」解法,在学完本节后,相应解法是很容易写出的。更多「拓扑排序」相关题目请参考「实战应用」。
Kahn
算法描述
Kahn算法 :基于 B F S BFS BFS 入度 这一概念很好地体现了「表述」,即当访问一个顶点 v v v 「入度」 为 0 ,即说明它所依赖的所有顶点一定已经被访问过了,此时即可将其输出 (将其排序)。具体来说,先计算所有顶点的入度,然后将入度为 0 的顶点放入队列中,从队列输出队首顶点并依次将其所有 邻接顶点入度减 1 ,每一个邻接顶点入度减 1 后,判断其入度是否减至 0 ,若为 0 将其入队。重复上述过程,直到队列为空 (所有顶点均已入队又出队) 。容易看出,一个顶点入度减至 0 ,当前仅当 它所依赖的顶点的入度在此之前已减至 0。算法结束时,顶点出队的顺序即为拓扑排序,这是一个 「顺序」 拓扑排序过程。
判圈: 某个节点出队时对其存在的邻边入度减 1 后,若这些邻边入度均未减至 0,则说明该图 有圈 。可以通过在 w h i l e while w hi l e 出队顶点数与总顶点数是否相等 来判圈。
A. B. Kahn于1962年发表的 Topological Sorting of Large Networks
算法过程
算法的详细过程如下,也即该算法求解拓扑排序问题时的编程范式。具体代码见「代码」部分,在参考之前,你应当通过此处给出的算法过程尝试自己写出。
根据输入建图及计算入度。
建图。
一般可用哈希表 M a p < k , v > Map<k, v> M a p < k , v > k k k v v v { 0 , 1 , 2 , . . . , n − 1 } \{0,1,2,...,n-1\} { 0 , 1 , 2 , ... , n − 1 } n n n List<List<Integer>> 存图效率更高,下标表示顶点,其对应的 List<Integer> 即为该顶点的邻接顶点表。通过下标可快速获取顶点的邻接表。
计算入度。
入度信息一般用大小为顶点数的数组 i n d e g r e e s [ ] indegrees[] in d e g rees [ ] ( u , v ) (u, v) ( u , v ) indegree[v]++ 。当所有边都被考察后,入度信息即已完备。
拓扑排序。
设置一个队列 q q q r e s res res c o u n t count co u n t
遍历 i n d e g r e e s indegrees in d e g rees 连通图 ,则 有且只有一个 顶点入度为 0,可在找到后立即跳出遍历)。
以一个 w h i l e while w hi l e u u u r e s res res count++ ,表明 u u u
遍历 u u u v v v v v v v v v
当 w h i l e while w hi l e 图有圈则存在入度不可能减至 0 的顶点 ,则已拓扑排序 (已出队) 的顶点个数 c o u n t count co u n t c o u n t = = n count == n co u n t == n
时空复杂度
时间复杂度:
建图及计算所有顶点入度需遍历所有边,时间复杂度为 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
队列中每个顶点均入队一次,出队一次,O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
更新并检查邻接顶点的 f o r for f or O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
故总的时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) 线性时间复杂度 。 若图是连通的 ,由于 ∣ E ∣ ≥ ∣ V ∣ |E| ≥ |V| ∣ E ∣ ≥ ∣ V ∣ ∣ E ∣ = ∣ V ∣ − 1 |E| = |V| - 1 ∣ E ∣ = ∣ V ∣ − 1 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) r e s / i n d e g r e e s res / indegrees res / in d e g rees O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
Kahn 拓扑排序算法实现 210. 课程表 II 。在掌握了 B F S BFS BFS
第一份代码以 哈希表 存图,适合于无法用连续的整数来表示顶点的场景。本题中,顶点可以被表示为 { 0 , 1 , 2 , 3 , . . . n − 1 } \{0, 1,2,3,...n - 1\} { 0 , 1 , 2 , 3 , ... n − 1 } 线性表 存图的代码效率更高。此写法为普遍的标准的 Kahn 拓扑排序写法,读者应对该写法 熟稔于心 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { public int [] findOrder(int numCourses, int [][] prerequisites) { int [] res = new int [numCourses], indegrees = new int [numCourses]; Map<Integer, List<Integer>> graph = new HashMap <>(); for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; List<Integer> adjs = graph.getOrDefault(u, new ArrayList <>()); adjs.add(v); graph.put(u, adjs); indegrees[v]++; } int count = 0 ; Queue<Integer> q = new ArrayDeque <>(); for (int u = 0 ; u < numCourses; u++){ if (indegrees[u] == 0 ) q.add(u); } while (!q.isEmpty()){ int u = q.remove(); res[count++] = u; List<Integer> adjs = graph.get(u); if (adjs != null ){ for (int v : adjs){ indegrees[v]--; if (indegrees[v] == 0 ) q.add(v); } } } return count == numCourses ? res : new int []{}; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { public int [] findOrder(int numCourses, int [][] prerequisites) { int [] res = new int [numCourses]; List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < numCourses; ++i){ graph.add(new ArrayList <>()); } int [] indegrees = new int [numCourses]; for (int [] edge : prerequisites){ int u = edge[1 ], v = edge[0 ]; indegrees[v]++; graph.get(u).add(v); } Queue<Integer> q = new ArrayDeque <>(); for (int u = 0 ; u < numCourses; ++u){ if (indegrees[u] == 0 ) q.add(u); } int count = 0 ; while (!q.isEmpty()){ int u = q.remove(); res[count] = u; count++; for (int v : graph.get(u)){ indegrees[v]--; if (indegrees[v] == 0 ) q.add(v); } } return count == numCourses ? res : new int []{}; } }
Tarjan (Topological Sorting)
算法描述
Tarjan拓扑排序算法 :基于 D F S DFS D FS v v v v v v d f s dfs df s v v v d f s dfs df s v v v 「缓存」 路径上 v v v v v v 递归栈的更靠顶部的空间中 (也就是在返回路径上) 缓存着。换句话说,我们只需要将 v v v v v v
顶点在算法过程中有三个状态, 未搜索,搜索中、已完成 (访问) 。算法从遍历顶点开始,每遇到一个「未搜索」的顶点 u u u d f s dfs df s d f s dfs df s u u u f o r for f or u u u v v v
若其状态为「未搜索」,对其递归调用 d f s dfs df s
若其状态为「搜索中」,表明我们此前进入过 v v v d f s dfs df s v v v v v v v v v h a s C y c l e hasCycle ha s C yc l e t r u e true t r u e
注意我们不必处理「已完成」的 v v v
如前一段所说,当 u u u d f s dfs df s h a s C y c l e hasCycle ha s C yc l e t r u e true t r u e
该算法并不总是被冠以 Tarjan 之名,在 wiki 中有下面这段话,注意「…seems to…」。另外,Cormen et al. (2001) 指的是那本著名的「算法导论」。
This depth-first-search-based algorithm is the one described by Cormen et al. (2001) , it seems to have been first described in print by Tarjan in 1976 .
※ 之所以称「Tarjan拓扑排序算法」而非「Tarjan算法」,是因为由 Tarjan 发明或合作发明或有重大贡献的算法和数据结构非常之多,如「最近公共祖先(LCA) 」、「强连通分量(SCC) 」、「伸展树 (Splay Tree) 」、「斐波那契堆 (Fibonacci Heaps) 」、「并查集 (Union-Find Set) 」等等。狭义上的「Tarjan算法」指的是「强连通分量」算法。实际上将基于 B F S BFS BFS D F S DFS D FS Does Tarjan’s SCC algorithm give a topological sort of the SCC? 。
… And his algorithm (SCC) also does topological sorting as a byproduct . ---- by Knuth
算法过程
算法的详细过程如下,也即该算法求解拓扑排序问题时的编程范式。具体代码见「代码」部分,在参考之前,你应当通过此处给出的算法过程尝试自己写出。
根据输入建图及准备 v i s i t e d visited v i s i t e d h a s C y c l e hasCycle ha s C yc l e r e s res res i d x idx i d x ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
建图。与 kahn 算法一致。
v i s i t e d visited v i s i t e d h a s C y c l e = f a l s e hasCycle = false ha s C yc l e = f a l se
拓扑排序。遍历所有顶点,对「未搜索」状态的顶点 u u u d f s dfs df s
进入 d f s dfs df s v i s i t e d [ u ] = 1 visited[u] = 1 v i s i t e d [ u ] = 1 u u u
以 f o r for f or u u u v v v
若 v i s i t e d [ v ] = = 0 visited[v] == 0 v i s i t e d [ v ] == 0 d f s dfs df s
若 v i s i t e d [ v ] = = 1 visited[v] == 1 v i s i t e d [ v ] == 1 v v v d f s dfs df s v v v v v v v v v h a s C y c l e hasCycle ha s C yc l e t r u e true t r u e
若 v i s i t e d [ v ] = = 2 visited[v] == 2 v i s i t e d [ v ] == 2
对于 u u u f o r for f or u u u
若能完成所有顶点的遍历而无圈,说明所有顶点已被拓扑排序,返回 r e s res res
时空复杂度
时间复杂度:
建图及需遍历所有边,时间复杂度为 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
每个顶点至多被标记两次,O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
检查邻接顶点的 f o r for f or O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
故总的时间复杂度为同 Kahn 算法一样也是线性时间复杂度 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) ∣ E ∣ ≥ ∣ V ∣ |E| ≥ |V| ∣ E ∣ ≥ ∣ V ∣ ∣ V ∣ = 2 |V| = 2 ∣ V ∣ = 2 ∣ E ∣ < ∣ V ∣ |E| < |V| ∣ E ∣ < ∣ V ∣ O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) r e s / v i s i t e d res / visited res / v i s i t e d O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
Tarjan 拓扑排序算法实现 210. 课程表 II 。此写法为普遍的标准的 Tarjan 拓扑排序写法,读者应对该写法 熟稔于心 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { List<List<Integer>> graph; int [] visited, res; boolean hasCycle = false ; int idx; public int [] findOrder(int numCourses, int [][] prerequisites) { this .graph = new ArrayList <>(); this .visited = new int [numCourses]; this .res = new int [numCourses]; this .idx = numCourses - 1 ; for (int i = 0 ; i < numCourses; i++) { graph.add(new ArrayList <>()); } for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; graph.get(u).add(v); } for (int u = 0 ; u < numCourses; u++){ if (visited[u] == 0 ) { dfs(u); if (hasCycle) return new int []{}; } } return res; } private void dfs (int u) { if (hasCycle) return ; visited[u] = 1 ; for (int v : graph.get(u)) { if (visited[v] == 0 ) dfs(v); else if (visited[v] == 1 ) { hasCycle = true ; return ; } } visited[u] = 2 ; res[idx--] = u; } }
拓扑排序判圈
在学习了本节内容后,我们再回到 684. 冗余连接 和 207. 课程表 这两题的,给出它们的拓扑排序解法。需要注意的是,应用 Kahn 拓扑排序时,对于「无向图」上的顶点,考虑的是无关方向的 「度」 ,开始排序时要将 度为 1 的顶点入队;对于「有向图」上的顶点,考虑的是 「入度」 ,开始排序时要将 入度为 0 的顶点入队。
无向图判圈
对于 684 题,因为题目要求返回构成圈的在 e d g e s edges e d g es e d g e s edges e d g es 若只要求判圈,那么也可以采用Tarjan拓扑排序算法 。如下我们只给出 Kahn 排序算法解 684 题的代码。
时间复杂度: 由于本题 ∣ V ∣ = ∣ E ∣ |V| = |E| ∣ V ∣ = ∣ E ∣ O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) e d g e s edges e d g es O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) d e g r e e s degrees d e g rees O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public int [] findRedundantConnection(int [][] edges) { int n = edges.length; int [] degrees = new int [n]; List<List<Integer>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : edges){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 ; degrees[u]++; degrees[v]++; graph.get(u).add(v); graph.get(v).add(u); } Queue<Integer> q = new ArrayDeque <>(); for (int i = 0 ; i < n; i++) { if (degrees[i] == 1 ) q.add(i); } while (!q.isEmpty()){ int u = q.remove(); for (int v : graph.get(u)){ degrees[v]--; if (degrees[v] == 1 ) q.add(v); } } for (int i = n - 1 ; i >= 0 ; i--){ int u = edges[i][0 ] - 1 , v = edges[i][1 ] - 1 ; if (degrees[u] > 1 && degrees[v] > 1 ){ return new int []{u + 1 , v + 1 }; } } return null ; } }
有向图判圈
对于 207. 课程表 题,其拓扑排序解法与 210. 课程表 II 题的区别仅在于前者无需真正排序,只需判断是否存在圈即可。以下给出 Kahn 和 Tarjan 两种拓扑排序算法的代码。
Kahn拓扑排序算法
时间复杂度: 拓扑排序时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) i n d e g r e e s indegrees in d e g rees O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution { public boolean canFinish (int numCourses, int [][] prerequisites) { List<List<Integer>> graph = new ArrayList <>(); int [] indegrees = new int [numCourses]; for (int i = 0 ; i < numCourses; i++) { graph.add(new ArrayList <>()); } for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; graph.get(u).add(v); indegrees[v]++; } Queue<Integer> q = new ArrayDeque <>(); for (int u = 0 ; u < numCourses; u++){ if (indegrees[u] == 0 ) q.add(u); } int count = 0 ; while (!q.isEmpty()){ int u = q.remove(); count++; for (int v : graph.get(u)){ indegrees[v]--; if (indegrees[v] == 0 ) q.add(v); } } return count == numCourses; } }
Tarjan拓扑排序算法
时间复杂度: 拓扑排序时间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d visited v i s i t e d O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { List<List<Integer>> graph; int [] visited; boolean hasCycle = false ; public boolean canFinish (int numCourses, int [][] prerequisites) { this .graph = new ArrayList <>(); this .visited = new int [numCourses]; for (int i = 0 ; i < numCourses; i++) { graph.add(new ArrayList <>()); } for (int [] edge : prerequisites){ int v = edge[0 ], u = edge[1 ]; graph.get(u).add(v); } for (int u = 0 ; u < numCourses; u++){ if (visited[u] == 0 ) { dfs(u); if (hasCycle) return false ; } } return true ; } private void dfs (int u) { if (hasCycle) return ; visited[u] = 1 ; for (int v : graph.get(u)) { if (visited[v] == 0 ) dfs(v); else if (visited[v] == 1 ) { hasCycle = true ; return ; } } visited[u] = 2 ; } }
小结
在本节中,我们分别介绍了基于 b f s bfs b f s d f s dfs df s 210. 课程表 II 一题的代码。我们还展示了利用「拓扑排序」,可以在「图判圈」这一问题上,实现线性时间复杂度求解,比「初探图搜索 (遍历)」一节的方法更好,显示了拓扑排序这一方法的优点。在之后的章节中,我们还会看到拓扑排序是如何继续发挥作用的。
最短路径
本节我们将学习图论算法中古老而经典的「最短路径 」问题,该算法在地图、交通等许多领域中的重要性无须多言。我们将按照如下三大类进行讲解。
无权单源最短路: (Single Source Shortest Path, SSSP) 给定一张无权图 G G G s s s s s s G G G
带权单源最短路: (Single Source Shortest Path, SSSP) 给定一张带权图 G G G s s s s s s G G G
带权全源最短路: (All Pairs Shortest Path, APSP) 给定一张带权图 G G G G G G
我们指出,除了特定情形的图 (如 DAG), 最短路径算法不区分图的边是否有向,建图时对有向图/无向图正确建图即可 (有向图单向建边,无向图双向建边)。为了使读者在学习过程中及时地得到反馈,我将在介绍每一种算法后,利用该算法实际解决如下对应题目。读者应当在理解算法内容之后尝试独立求解,然后再与文中给出的代码相比照。
无权单源最短路
我们首先介绍最简单的「无权单源最短路」,力扣上似乎没有相应的题目,不过力扣友商平台上的 814.无向图中的最短路径 一题比较匹配 (请自行搜索),我们通过这题来学习本节。虽然该题只须求给定两点之间的最短距离,但我们仍然按给定一点 (源点 s s s
需要注意的是,本小节给出的例题的图虽是无向图,但有向图解法是一致的。「有向无权单源最短路」与「无向无权单源最短路」的求解方法的唯一区别只在与建图时是双向建边 (无向图) 还是单向 (有向图) 建边。后续「带权图」的最短路问题也一样,有向无向并不影响算法过程,因此 对于「最短路」问题,通常不强调「无向」还是「有向」 。
朴素版
虽然我们早已熟悉利用队列来辅助 b f s bfs b f s 朴素版本 ,以此为契机再次感受使用队列实现 b f s bfs b f s
算法描述
在熟悉 b f s bfs b f s s s s b f s bfs b f s s s s f o r for f or for(int dist = 0; dist < |V| - 1; dist++) ,d i s t = 0 dist = 0 d i s t = 0 f o r for f or f o r for f or 遍历所有顶点 ,找到那些 距离已确定 且为当前 d i s t dist d i s t u u u u u u f o r for f or v v v 距离未确定 的 v v v d i s t + 1 dist + 1 d i s t + 1
具体来说,对于 s s s f o r for f or s s s 邻接顶点 的距离 +1,(如果要求返回具体路径,可以在此时将其前驱顶点置为 s s s u u u 距离未确定 的邻接顶点 v v v v v v v v v u u u f o r for f or d i s t = 0 dist = 0 d i s t = 0 d i s t + 1 dist+1 d i s t + 1 ≤ ∣ V ∣ − 1 ≤|V|-1 ≤ ∣ V ∣ − 1 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1
算法过程
设置一个用于泛洪标记 (访问状态) 的 v i s i t e d visited v i s i t e d d i s t s dists d i s t s
置给定源点 s s s A A A
外层 (第一层) f o r for f or d i s t = 0 dist=0 d i s t = 0 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 d i s t dist d i s t ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1
第二层 f o r for f or d i s t dist d i s t u u u
第三层 f o r for f or u u u v v v v v v d i s t + 1 dist+1 d i s t + 1 v v v u u u
最外层 f o r for f or
※ 该题的输入中,顶点的 l a b e l label l ab e l v i s i t e d visited v i s i t e d d i s t s dists d i s t s
时空复杂度
时间复杂度:虽然程序有三层循环,但总体的效果是对所有顶点询问一次它们的邻接顶点,并不总能进入第三层,因此时间复杂度取决于前两层 f o r for f or O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d / d i s t s visited/dists v i s i t e d / d i s t s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public class Solution { public int shortestPath (List<UndirectedGraphNode> graph, UndirectedGraphNode A, UndirectedGraphNode B) { if (A == B) return 0 ; int n = graph.size(), a = A.label, b = B.label; Set<Integer> visited = new HashSet <>(); Map<Integer, Integer> dists = new HashMap <>(); dists.put(a, 0 ); visited.add(a); for (int dist = 0 ; dist < n - 1 ; dist++){ for (UndirectedGraphNode uNode : graph){ int u = uNode.label; if (visited.contains(u) && dists.get(u) == dist){ for (UndirectedGraphNode vNode : uNode.neighbors){ int v = vNode.label; if (!visited.contains(v)) { dists.put(v, dist + 1 ); visited.add(v); } } } } } return visited.contains(b) ? dists.get(b) : -1 ; } }
队列优化版
算法描述
朴素版做法的明显缺点是在程序运行到后期,大部分顶点的距离已确定,但每次距离加 1 后,仍要遍历所有顶点,我们已经知道使用队列可以优化这部分时间。从源点 s s s b f s bfs b f s s s s f o r for f or u u u v v v v v v v v v q q q s s s
算法过程
设置一个队列 q q q v i s i t e d visited v i s i t e d d i s t s dists d i s t s
首先将源点 s s s
执行 w h i l e ( ! q . i s E m p t y ( ) ) while(!q.isEmpty()) w hi l e ( ! q . i s E m pt y ( )) b f s bfs b f s f o r for f or 一层 顶点,d i s t + + dist++ d i s t + +
对每一个当前层的顶点 u u u f o r for f or v v v v v v v v v
当 q q q s s s
时空复杂度
时间复杂度: B F S BFS BFS O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度: 存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d / d i s t s / q visited/dists/q v i s i t e d / d i s t s / q O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
代码
给出如下代码。由于该题的输入中,顶点的 l a b e l label l ab e l v i s i t e d visited v i s i t e d d i s t s dists d i s t s g r a p h graph g r a p h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class Solution { public int shortestPath (List<UndirectedGraphNode> graph, UndirectedGraphNode A, UndirectedGraphNode B) { if (A == B) return 0 ; int n = graph.size(), dist = 0 , a = A.label, b = B.label; Set<Integer> visited = new HashSet <>(); HashMap<Integer, Integer> dists = new HashMap <>(); Queue<UndirectedGraphNode> q = new ArrayDeque <>(); q.add(A); visited.add(a); while (!q.isEmpty()){ dist++; int size = q.size(); for (int i = 0 ; i < size; i++){ UndirectedGraphNode uNode = q.remove(); for (UndirectedGraphNode vNode : uNode.neighbors){ int v = vNode.label; if (!visited.contains(v)){ dists.put(v, dist); q.add(vNode); visited.add(v); } } } } return visited.contains(b) ? dists.get(b) : -1 ; } }
如果只是为了求解该题,无需记录所有顶点的距离,只要遇到顶点 B B B v i s i t e d visited v i s i t e d
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class Solution { public int shortestPath (List<UndirectedGraphNode> graph, UndirectedGraphNode A, UndirectedGraphNode B) { if (A == B) return 0 ; int n = graph.size(), dist = 0 ; boolean [] visited = new boolean [n + 1 ]; Queue<UndirectedGraphNode> q = new ArrayDeque <>(); q.add(A); visited[A.label] = true ; while (!q.isEmpty()){ dist++; int size = q.size(); for (int i = 0 ; i < size; i++){ UndirectedGraphNode uNode = q.remove(); for (UndirectedGraphNode vNode : uNode.neighbors){ int v = vNode.label; if (vNode == B) return dist; else if (!visited[v]){ q.add(vNode); visited[v] = true ; } } } } return -1 ; } }
带权单源最短路
当图为有权图时,我们将无法简单地通过层数增加来确定每一层顶点的距离,因为从源点若有多条路径可到达顶点 v v v 「带权单源最短路」 算法来求解经典的带权单源最短路问题 743. 网络延迟时间 。再次强调,图「有向」或「无向」,对于这些算法,区别仅在于建图时为双向边还是单向边,除非特别说明 (例如 DAG ),否则 最短路算法不区分有向图或是无向图 。
Dijkstra
一种基于贪心思想的求解 无负边图单源最短路径 的算法 (后续会说明为何不适用于负边图)。该算法可能是「最短路」算法家族中最知名的一个。Dijkstra 算法提出年代早,为贪心思想的极佳应用,另外,其在「20分钟」内被发明的故事也为人所乐道,具体可看相关 wiki 词条。
Dijkstra 在1956年构思出此算法,并于1959年发表的 A Note on Two Problems in Connexion with Graphs
本节中,我将仍旧先给出「朴素版」,专注学习 Dijkastra 的过程,并给出严谨的正确性证明。随后,我们提出应用 「优先队列」 的改进版,并通过对这两个版本时间复杂度的分析,指出对于「稠密图」,应当使用「朴素版」,对于「稀疏图」,应当使用「优先队列版」。接着,我会以一个小例子直观地展示为何 Dijkstra 无法处理具有负边的图。
朴素版
算法描述
Dijkstra算法 (狄杰斯特拉) : Dijkstra 算法的 基本操作 是将所有顶点区分为距离 已确定 和 未确定 的顶点。算法开始前所有顶点的距离均未确定(一般置为I n f i n i t y Infinity I n f ini t y s s s w h i l e while w hi l e 是否有距离未确定 的顶点,若有则将 其中距离最小者 u u u 当前顶点 ,并使其距离已知 。然后以 b f s bfs b f s u u u v v v v v v u u u s s s
松弛操作 (relax) 是 Dijkstra 算法的关键,也是后续其他最短路径算法的关键。「松弛」指的是在确定当前顶点 u u u v v v d u + ∣ ( u , v ) ∣ < d v du + |(u,v)| < dv d u + ∣ ( u , v ) ∣ < d v u u u v v v v v v v v v
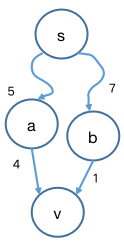
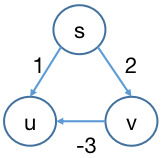
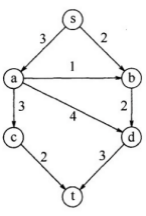
s s s a a a b b b a a a b b b c c c d v = I n i f i n i t y dv = Inifinity d v = I ni f ini t y d a = 5 da = 5 d a = 5 d b = 7 db = 7 d b = 7
松弛顺序为先 a a a b b b
a a a d a + ∣ ( a , v ) ∣ = 9 < I n f i n i t y da + |(a, v)| = 9 < Infinity d a + ∣ ( a , v ) ∣ = 9 < I n f ini t y a a a d v dv d v v v v a a a b b b d b + ∣ ( b , v ) ∣ = 8 < 9 db + |(b, v)| = 8 < 9 d b + ∣ ( b , v ) ∣ = 8 < 9 b b b d v dv d v v v v b b b
松弛顺序为先 b b b a a a
b b b d b + ∣ ( b , v ) ∣ = 8 < I n f i n i t y db + |(b, v)| = 8 < Infinity d b + ∣ ( b , v ) ∣ = 8 < I n f ini t y b b b d v dv d v v v v b b b a a a d a + ∣ ( a , v ) ∣ = 9 > = 8 da + |(a, v)| = 9 >= 8 d a + ∣ ( a , v ) ∣ = 9 >= 8 a a a d v dv d v
通过这个例子我们能够直观地观察到,来自 v v v d v dv d v
至此我们已能够理解如下内容。Dijkstra 算法分成 ∣ V ∣ |V| ∣ V ∣ v v v d v dv d v s s s ∣ V ∣ |V| ∣ V ∣ 「贪心」 的体现,其正确性在于,之后不可能通过除 v v v v v v d v dv d v I n f i n i t y Infinity I n f ini t y d v dv d v
算法过程
建图及初始化。
构建带权图。
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ b o o l e a n boolean b oo l e an v i s i t e d [ ] visited[] v i s i t e d [ ]
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] s s s I n f i n i t y Infinity I n f ini t y s s s
置 s s s
以一个循环寻找 当前距离未确定顶点中距离最小者 u u u u u u
松弛操作。尝试松弛 u u u 距离未确定的 邻接顶点 v v v d v dv d v d v = m i n { d v , d u + ∣ ( u , v ) ∣ } dv = min\{dv, du + |(u,v)|\} d v = min { d v , d u + ∣ ( u , v ) ∣ } v v v u u u
循环结束时,每个顶点到源点的最短路径距离被求出。
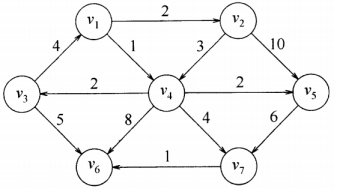
设下图 v 1 v_1 v 1
阶段
距离已确定
距离未确定 (括号内表示距离)
松弛
初始
v 1 ( ∞ ) v_1(∞) v 1 ( ∞ ) v 2 ( ∞ ) v_2(∞) v 2 ( ∞ ) v 3 ( ∞ ) v_3(∞) v 3 ( ∞ ) v 4 ( ∞ ) v_4(∞) v 4 ( ∞ ) v 5 ( ∞ ) v_5(∞) v 5 ( ∞ ) v 6 ( ∞ ) v_6(∞) v 6 ( ∞ ) v 7 ( ∞ ) v_7(∞) v 7 ( ∞ ) v 1 ( 0 ) v_1(0) v 1 ( 0 )
1
v 1 ( 0 ) v_1(0) v 1 ( 0 ) v 2 ( ∞ ) v_2(∞) v 2 ( ∞ ) v 3 ( ∞ ) v_3(∞) v 3 ( ∞ ) v 4 ( ∞ ) v_4(∞) v 4 ( ∞ ) v 5 ( ∞ ) v_5(∞) v 5 ( ∞ ) v 6 ( ∞ ) v_6(∞) v 6 ( ∞ ) v 7 ( ∞ ) v_7(∞) v 7 ( ∞ ) v 2 ( 2 ) , v_2(2), v 2 ( 2 ) , v 4 ( 1 ) v_4(1) v 4 ( 1 )
2
v 4 ( 1 ) v_4(1) v 4 ( 1 ) v 2 ( 2 ) v_2(2) v 2 ( 2 ) v 3 ( ∞ ) v_3(∞) v 3 ( ∞ ) v 5 ( ∞ ) v_5(∞) v 5 ( ∞ ) v 6 ( ∞ ) v_6(∞) v 6 ( ∞ ) v 7 ( ∞ ) v_7(∞) v 7 ( ∞ ) v 3 ( 3 ) v_3(3) v 3 ( 3 ) v 5 ( 3 ) v_5(3) v 5 ( 3 ) v 6 ( 9 ) v_6(9) v 6 ( 9 ) v 7 ( 5 ) v_7(5) v 7 ( 5 )
3
v 2 ( 2 ) v_2(2) v 2 ( 2 ) v 3 ( 3 ) v_3(3) v 3 ( 3 ) v 5 ( 3 ) v_5(3) v 5 ( 3 ) v 6 ( 9 ) v_6(9) v 6 ( 9 ) v 7 ( 5 ) v_7(5) v 7 ( 5 )
4
v 3 ( 3 ) v_3(3) v 3 ( 3 ) v 5 ( 3 ) v_5(3) v 5 ( 3 ) v 6 ( 9 ) v_6(9) v 6 ( 9 ) v 7 ( 5 ) v_7(5) v 7 ( 5 ) v 6 ( 8 ) v_6(8) v 6 ( 8 )
5
v 5 ( 3 ) v_5(3) v 5 ( 3 ) v 6 ( 8 ) v_6(8) v 6 ( 8 ) v 7 ( 5 ) v_7(5) v 7 ( 5 )
6
v 7 ( 5 ) v_7(5) v 7 ( 5 ) v 6 ( 8 ) v_6(8) v 6 ( 8 ) v 6 ( 5 ) v_6(5) v 6 ( 5 )
7
v 6 ( 5 ) v_6(5) v 6 ( 5 )
正确性证明
如下,利用数学归纳法 (结合反证法) 严格证明 Dijkstra 算法正确性。
本证明参考了这个帖子 。
a) 首先回顾数学归纳法的证明过程。
起始验证。对于命题 P ( n ) P(n) P ( n ) n = 1 n = 1 n = 1 P P P
假设命题成立。即假设命题 P ( n ) P(n) P ( n ) n = m ( m > 1 , m ∈ N ) n = m (m > 1, m ∈ N) n = m ( m > 1 , m ∈ N )
递推证明。根据 2 的假设,若能证明 n = m + 1 n = m + 1 n = m + 1 P P P
例如,有命题 P : 1 + 2 + 3... + n = n ∗ ( n + 1 ) / 2 P:1+2+3...+n = n*(n+1)/2 P : 1 + 2 + 3... + n = n ∗ ( n + 1 ) /2
起始验证。当 n n n 1 1 1 1 = 1 ∗ ( 1 + 1 ) / 2 1 = 1*(1+1)/2 1 = 1 ∗ ( 1 + 1 ) /2
假设命题成立。假设命题等于 m m m 1 + 2 + 3 + . . . + m = m ∗ ( m + 1 ) / 2 1+2+3+...+m = m*(m+1)/2 1 + 2 + 3 + ... + m = m ∗ ( m + 1 ) /2
递推证明。根据 2 的假设,如果能证明 n = m + 1 n = m+1 n = m + 1 P P P
证明:在 2 所示式子左右两边加上 m + 1 m+1 m + 1 1 + 2 + 3 + . . . + m + ( m + 1 ) = m ∗ ( m + 1 ) / 2 + ( m + 1 ) 1+2+3+...+m+(m+1) = m*(m+1)/2 + (m+1) 1 + 2 + 3 + ... + m + ( m + 1 ) = m ∗ ( m + 1 ) /2 + ( m + 1 )
等号右边可以写成 ( m + 1 ) ∗ ( m + 2 ) / 2 (m+1)*(m+2)/2 ( m + 1 ) ∗ ( m + 2 ) /2 n = m + 1 n = m+1 n = m + 1 P P P
b) 利用数学归纳法证明如下命题。
命题 P P P n n n w h i l e wh ile w hi l e n n n A A A ∀ v ∈ A ( ∀v ∈ A( ∀ v ∈ A ( n n n d v = δ v dv = δv d v = δ v
※ d v dv d v tentative shortest distance ),对于源点 s s s d s = 0 ds = 0 d s = 0 δ v δv δ v v v v
起始验证。当 n n n 1 1 1 A A A s s s d s = 0 ds = 0 d s = 0 δ v = 0 δv = 0 δ v = 0 n = 1 n=1 n = 1
假设命题成立。假设命题 P P P n n n m m m P ( m ) P(m) P ( m ) m m m m m m A A A ∀ v ∈ A ∀v ∈ A ∀ v ∈ A m m m d v = δ v dv = δv d v = δ v
P ( m + 1 ) P(m+1) P ( m + 1 ) m + 1 m+1 m + 1 u u u A A A d u = δ u du = δu d u = δ u P P P
更详细地,∣ A ∣ = m |A| = m ∣ A ∣ = m B ( B = S − A ) B (B = S - A) B ( B = S − A ) u u u m + 1 m+1 m + 1 A A A ∣ A ∣ = m + 1 |A| = m + 1 ∣ A ∣ = m + 1 d u = δ u du = δu d u = δ u P ( m + 1 ) P(m+1) P ( m + 1 ) ∀ v ∈ A ∀v ∈ A ∀ v ∈ A m + 1 m+1 m + 1 d v = δ v dv = δv d v = δ v
以反证法证明之。
3.1 假设 m + 1 m+1 m + 1 d u = δ u du = δu d u = δ u
(1) δ u < d u δu < du δ u < d u
※ δ u δu δ u u u u d u = δ u du = δu d u = δ u δ u < d u δu < du δ u < d u s s s u u u δ u δu δ u
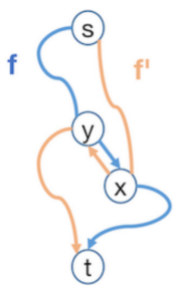
3.2 根据3.1的假设,存在一条从源点 s s s u u u P u Pu P u s s s u u u ∣ P u ∣ = δ u < d u |Pu| = δu < du ∣ P u ∣ = δ u < d u P u Pu P u A A A u u u A A A A A A s s s A A A P u Pu P u x x x y y y x x x A A A s s s y y y B B B u u u y y y u u u A A A P x Px P x P u Pu P u x x x P x + ( x , y ) Px + (x, y) P x + ( x , y ) P u Pu P u
(2) ∣ P x ∣ + ∣ ( x , y ) ∣ ≤ ∣ P u ∣ = δ u |Px| + |(x, y)| ≤ |Pu| = δu ∣ P x ∣ + ∣ ( x , y ) ∣ ≤ ∣ P u ∣ = δ u
这是显然的,因为 P x + ( x , y ) Px + (x, y) P x + ( x , y ) P u Pu P u y = u y=u y = u
3.3 在 x x x A A A y y y 松弛操作 ,该操作会比较 d x + ∣ ( x , y ) ∣ dx + |(x, y)| d x + ∣ ( x , y ) ∣ d y dy d y d x + ∣ ( x , y ) ∣ dx + |(x, y)| d x + ∣ ( x , y ) ∣ d y dy d y d y = d x + ∣ ( x , y ) ∣ dy = dx + |(x, y)| d y = d x + ∣ ( x , y ) ∣ d y < d x + ∣ ( x , y ) ∣ dy < dx + |(x, y)| d y < d x + ∣ ( x , y ) ∣ y y y y y y d y dy d y A A A d y dy d y
(3) d y ≤ d x + ∣ ( x , y ) ∣ dy ≤ dx + |(x, y)| d y ≤ d x + ∣ ( x , y ) ∣
比较式 (2) 和式 (3) 中的 ∣ P x ∣ |Px| ∣ P x ∣ d x dx d x d x = δ x dx = δx d x = δ x P ( m ) P(m) P ( m ) x x x P ( m ) P(m) P ( m ) m m m P x Px P x s s s x x x d ( x ) ≤ ∣ P x ∣ d(x) ≤ |Px| d ( x ) ≤ ∣ P x ∣ P x Px P x s s s x x x
d y ≤ d x + ∣ ( x , y ) ∣ ≤ ∣ P x ∣ + ∣ ( x , y ) ∣ ≤ ∣ P u ∣ dy ≤ dx + |(x, y)| ≤ |Px| + |(x, y)| ≤ |Pu| d y ≤ d x + ∣ ( x , y ) ∣ ≤ ∣ P x ∣ + ∣ ( x , y ) ∣ ≤ ∣ P u ∣
(4) d y ≤ ∣ P u ∣ = δ u dy ≤ |Pu| = δu d y ≤ ∣ P u ∣ = δ u
3.4 顶点 y y y u u u B B B u u u m + 1 m+1 m + 1 A A A m + 1 m+1 m + 1 u u u B B B B B B y y y s s s
(5) d u ≤ d y du ≤ dy d u ≤ d y
结合式 (1),式 (4),式 (5) 得到:
(6) δ u < d u ≤ d y ≤ ∣ P u ∣ = δ u δu < du ≤ dy ≤ |Pu| = δu δ u < d u ≤ d y ≤ ∣ P u ∣ = δ u δ u < δ u δu < δu δ u < δ u
至此,由 3.1 的假设 「d ( u ) = δ ( u ) d(u) = δ(u) d ( u ) = δ ( u ) d ( u ) = δ ( u ) d(u) = δ(u) d ( u ) = δ ( u ) Dijkstra 算法正确性得证 。
时空复杂度
时间复杂度:O ( ∣ V ∣ 2 + ∣ E ∣ ) O(|V|^2 + |E|) O ( ∣ V ∣ 2 + ∣ E ∣ ) ∣ E ∣ < ∣ V ∣ 2 |E| < |V|^2 ∣ E ∣ < ∣ V ∣ 2 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
寻找拥有最小距离的顶点的时间为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) ∣ V ∣ |V| ∣ V ∣
所有顶点的距离被松弛的次数上限为 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) ∣ E ∣ |E| ∣ E ∣ O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
空间复杂度:存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d / d i s t s visited/dists v i s i t e d / d i s t s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
现在,我们利用上述知识来实际编程解决 743. 网络延迟时间 。仔细读题后可知,从某个节点 k k k k k k k k k k k k
构建带权图时,需要记录边权,因此顶点的邻接表以 List<int[]> 表示,对于顶点 u u u int[] v_weight ,v_weight[0] 为 u u u v_weight[1] 为边权 ∣ ( u , v ) ∣ |(u, v)| ∣ ( u , v ) ∣
为了清晰地看出「在当前距离未确定的顶点中找到距离最小者」这一「贪心」动作,我们将其写为 g e t M i n getMin g e tM in
当存在与源点不连通的顶点时,该顶点的距离将得不到松弛,因此存在未松弛顶点时返回 -1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { public int networkDelayTime (int [][] times, int n, int k) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; boolean [] visited = new boolean [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; int u = -1 ; while ((u = getMin(dists, visited)) != -1 ) { visited[u] = true ; for (int [] v_weight : graph.get(u)) { int v = v_weight[0 ], weight = v_weight[1 ]; if (!visited[v]) { int dv = dists[u] + weight; if (dv < dists[v]) { dists[v] = dv; } } } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } private int getMin (int [] dists, boolean [] visited) { int n = dists.length, min = Integer.MAX_VALUE, minVertex = -1 ; for (int u = 0 ; u < n; u++) { if (!visited[u] && dists[u] < min) { min = dists[u]; minVertex = u; } } return minVertex; } }
优先队列版
算法描述
针对朴素版「算法过程」第 2 步「在当前距离未确定顶点中寻找距离最小者」,我们很容易想到利用优先队列 (小顶堆) p q ( p r i o r i t y _ q u e u e ) pq(priority\_queue) pq ( p r i or i t y _ q u e u e ) v v v p q pq pq
算法过程
建图及初始化。
构建带权图。
设置一个小顶堆 p q pq pq
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ b o o l e a n boolean b oo l e an v i s i t e d [ ] visited[] v i s i t e d [ ]
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] s s s I n f i n i t y Infinity I n f ini t y s s s
置 s s s
s s s
一次出堆完成一个顶点最短路径的确定。以 w h i l e while w hi l e p q pq pq u u u u u u u u u
松弛操作。尝试松弛 u u u 距离未确定的 邻接顶点 v v v d v dv d v d v = m i n { d v , d u + ∣ ( u , v ) ∣ } dv = min\{dv, du + |(u,v)|\} d v = min { d v , d u + ∣ ( u , v ) ∣ } v v v u u u
循环结束时,每个顶点到源点的最短路径距离被求出。
时空复杂度
时间复杂度:O ( ∣ E ∣ l o g ∣ E ∣ + ∣ E ∣ l o g ∣ E ∣ ) O(|E|log|E|+|E|log|E|) O ( ∣ E ∣ l o g ∣ E ∣ + ∣ E ∣ l o g ∣ E ∣ ) O ( ∣ E ∣ l o g ∣ E ∣ ) O(|E|log|E|) O ( ∣ E ∣ l o g ∣ E ∣ ) O ( ∣ E ∣ l o g ∣ V ∣ ) O(|E|log|V|) O ( ∣ E ∣ l o g ∣ V ∣ )
在当前距离未确定顶点中寻找距离最小者的总时间复杂度 为 O ( ∣ E ∣ l o g ∣ E ∣ ) O(|E|log|E|) O ( ∣ E ∣ l o g ∣ E ∣ )
w h i l e while w hi l e p q pq pq O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) 获取距离最小者耗时为堆的查找时间复杂度, O ( l o g ∣ E ∣ ) O(log|E|) O ( l o g ∣ E ∣ )
故此部分时间复杂度为 O ( ∣ E ∣ l o g ∣ E ∣ ) O(|E|log|E|) O ( ∣ E ∣ l o g ∣ E ∣ )
※ 优先队列判空操作 i s E m p t y ( ) isEmpty() i s E m pt y ( ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
考虑所有顶点的距离被更新 (松弛) 导致的 总的顶点入堆时间复杂度 为 O ( ∣ E ∣ l o g ( ∣ E ∣ ) ) O(|E|log(|E|)) O ( ∣ E ∣ l o g ( ∣ E ∣ ))
由算法可知顶点 u u u v v v u u u u u u v v v u u u 当前距离被确定的顶点 的所有出边。所有顶点的出边即总边数为 ∣ E ∣ |E| ∣ E ∣ O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
d v dv d v v v v O ( l o g ∣ E ∣ ) O(log|E|) O ( l o g ∣ E ∣ ) 所有顶点的距离更新 以及该更新导致的 顶点入堆的总时间复杂度 为 O ( ∣ E ∣ + ∣ E ∣ l o g ∣ E ∣ ) O(|E| + |E|log|E|) O ( ∣ E ∣ + ∣ E ∣ l o g ∣ E ∣ )
※ 根据上述顶点入堆次数取决于总边数的分析,堆的大小上限不是 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) d v dv d v v v v O ( l o g ∣ E ∣ ) O(log|E|) O ( l o g ∣ E ∣ ) O ( l o g ∣ V ∣ ) O(log|V|) O ( l o g ∣ V ∣ ) ∣ E ∣ < ∣ V ∣ 2 |E| < |V|^2 ∣ E ∣ < ∣ V ∣ 2 l o g ∣ E ∣ < 2 l o g ∣ V ∣ log|E| < 2log|V| l o g ∣ E ∣ < 2 l o g ∣ V ∣ O ( l o g ∣ V ∣ ) O(log|V|) O ( l o g ∣ V ∣ )
空间复杂度:存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d / d i s t s visited/dists v i s i t e d / d i s t s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) p q pq pq O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
※ tip1: 连通图顶点数与边数有如下关系。
无向连通图:∣ V ∣ − 1 < = ∣ E ∣ < = ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) / 2 |V| - 1 <= |E| <= |V|*(|V| - 1) / 2 ∣ V ∣ − 1 <= ∣ E ∣ <= ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) /2
链状时 ∣ E ∣ |E| ∣ E ∣ ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) / 2 |V|*(|V| - 1) / 2 ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) /2
有向连通图:∣ V ∣ − 1 < = ∣ E ∣ < = ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) |V| - 1 <= |E| <= |V|*(|V| - 1) ∣ V ∣ − 1 <= ∣ E ∣ <= ∣ V ∣ ∗ ( ∣ V ∣ − 1 )
链状时 ∣ E ∣ |E| ∣ E ∣ ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 ∣ V ∣ ∗ ( ∣ V ∣ − 1 ) |V|*(|V| - 1) ∣ V ∣ ∗ ( ∣ V ∣ − 1 )
※ 利用 Fibonacci堆的 Dijkstra 算法时间复杂度为 O ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ ) O(|E|+|V|log|V|) O ( ∣ E ∣ + ∣ V ∣ l o g ∣ V ∣ )
对比「朴素版」的时间复杂度,不难看出,当图为 「稠密图」 时,「优先队列版」复杂度可表为 O ( ∣ V ∣ 2 l o g ∣ V ∣ ) O(|V|^2log|V|) O ( ∣ V ∣ 2 l o g ∣ V ∣ ) 「稀疏图」 时,「优先队列版」复杂度可表为 O ( ∣ V ∣ l o g ∣ V ∣ ) O(|V|log|V|) O ( ∣ V ∣ l o g ∣ V ∣ )
代码
现在,我们给出如下利用优先队列的 Dijkstra 算法代码来解决 743. 网络延迟时间 。其与朴素版的差别仅在于每个「阶段」寻找当前距离未确定顶点中距离最小者的方式不同。该写法为 Dijkstra 算法写法的模版写法,读者应 牢记于心 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public int networkDelayTime (int [][] times, int n, int k) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; boolean [] visited = new boolean [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; PriorityQueue<int []> pq = new PriorityQueue <>(((u, v) -> u[1 ] - v[1 ])); pq.add(new int []{k - 1 , 0 }); while (!pq.isEmpty()) { int [] u_dist = pq.remove(); int u = u_dist[0 ]; visited[u] = true ; for (int [] v_weight : graph.get(u)) { int v = v_weight[0 ], weight = v_weight[1 ]; if (!visited[v]) { int dv = dists[u] + weight; if (dv < dists[v]) { dists[v] = dv; pq.add(new int []{v, dv}); } } } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { public int networkDelayTime (int [][] times, int n, int k) { int m = times.length, edgeNum = 0 ; int [] heads = new int [n]; int [] ends = new int [m + 1 ], nexts = new int [m + 1 ], weights = new int [m + 1 ]; for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; edgeNum++; weights[edgeNum] = weight; ends[edgeNum] = v; nexts[edgeNum] = heads[u]; heads[u] = edgeNum; } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; boolean [] visited = new boolean [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; PriorityQueue<int []> pq = new PriorityQueue <>(((u, v) -> u[1 ] - v[1 ])); pq.add(new int []{k - 1 , 0 }); while (!pq.isEmpty()) { int u = pq.remove()[0 ]; if (visited[u]) continue ; visited[u] = true ; for (int edgeNo = heads[u]; edgeNo != 0 ; edgeNo = nexts[edgeNo]) { int v = ends[edgeNo], weight = weights[edgeNo]; if (!visited[v]) { int dv = dists[u] + weight; if (dv < dists[v]) { dists[v] = dv; pq.add(new int []{v, dv}); } } } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } }
负边图
以下图为例说明 Dijkstra 算法为何无法处理负边图。
顶点 s s s s s s d u du d u d v dv d v u u u v v v d u du d u u u u d u = 1 du = 1 d u = 1 s s s v v v u u u
由此我们也可以看到,Dijkstra 「贪心」能够成立的一个隐含前提是路径边数的增长 必须 使得路径长 (边权和) 是 「非递减」 的。存在负边则导致路径边数增长后边权和递减,使得「贪心」成立的前提不成立。
DAG SSSP
算法描述
若最短路的求解对象是 DAG ,那么根据其无圈的特点,可以采用「拓扑排序」的方式求单源最短路,使得时间复杂度仅为线性的 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
有向无圈图 一定存在拓扑排序,从一个入度为 0 的源点 s s s q q q s s s w h i l e ( ! q . i s E m p t y ( ) ) while(!q.isEmpty()) w hi l e ( ! q . i s E m pt y ( )) u u u d u du d u d u du d u u u u 入队 时其距离即确定。
有负边的 DAG
DAG版的 Dijkstra 算法 可应用于有负边的DAG。 因为对任意顶点 u u u u u u d u du d u s s s s s s d u du d u d v dv d v u , v u, v u , v v v v d v = 2 dv = 2 d v = 2 v v v v v v v v v d u du d u u u u u u u d u = − 1 du = -1 d u = − 1 u u u 在其入度减至 0 的过程中总会更新至最短 。
贪心 & 动态规划
这个小部分是我的一点思考🤔,与读者们探讨一下 Dijkstra 和 DAG 拓扑排序式的 SSSP 算法所分别体现的「贪心」和「动态规划」思想。
我们已经知道,无论是一般的 Dijkstra 还是本节的 DAG 上的 SSSP 算法,在求顶点 v v v ( u , v ) (u, v) ( u , v ) v v v
d v = m i n { d v , d u + ∣ ( u , v ) ∣ } , ( u , v ) ∈ E dv = min\{dv, du + |(u, v)|\}, (u, v) ∈ E
d v = min { d v , d u + ∣ ( u , v ) ∣ } , ( u , v ) ∈ E
主要区别在于,在 Dijkstra 中,我们不必 「全部算完」 所有入边带来的松弛,而是在 d v dv d v
算法过程
建图及初始化。
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ i n d e g r e e s [ ] indegrees[] in d e g rees [ ]
构建带权图并同时计算入度。
设置一个队列 q q q
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] s s s I n f i n i t y Infinity I n f ini t y s s s
置 s s s
s s s
通过 w h i l e ( ! q . i s E m p t y ( ) ) while(!q.isEmpty()) w hi l e ( ! q . i s E m pt y ( ))
松弛操作。尝试松弛 u u u 距离未确定的 邻接顶点 v v v d v dv d v d v = m i n { d v , d u + ∣ ( u , v ) ∣ } dv = min\{dv, du + |(u,v)|\} d v = min { d v , d u + ∣ ( u , v ) ∣ } v v v u u u
将上述 v v v v v v v v v
循环结束时,每个顶点到源点的最短路径距离被求出。
时空复杂度
时间复杂度:即拓扑排序的时间复杂度,为线性时间复杂度 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度:存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) v i s i t e d / d i s t s visited/dists v i s i t e d / d i s t s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) q q q O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
如下是假设 743. 网络延迟时间 的输入为无圈图的前提下的代码。但实际部分测试用例是有圈的,测试了一下只能过 15 个用例,然后就碰到有圈图了。等找到合适的输入限制为 DAG 图的题之后再更新。总之,DAG 上「拓扑排序」式的 SSSP 算法,或者干脆称 DAG 版的 Dijkstra 算法的写法如下。如果我们确定输入为 DAG,则应该优先考虑此版本算法, 以获得线性时间复杂度 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public int networkDelayTime (int [][] times, int n, int k) { List<List<int []>> graph = new ArrayList <>(); int [] indegrees = new int [n]; for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); indegrees[v]++; } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; Queue<Integer> q = new ArrayDeque <>(); q.add(k - 1 ); while (!q.isEmpty()) { int u = q.remove(); for (int [] v_weight : graph.get(u)) { int v = v_weight[0 ], weight = v_weight[1 ]; int dv = dists[u] + weight; if (dv < dists[v]) { dists[v] = dv; } indegrees[v]--; if (indegrees[v] == 0 ) q.add(v); } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } }
Bellman-Ford
之前我们指出,Dijkstra 算法因其「贪心」的特点,在还未穷尽顶点所有入边的松弛时就「过早地」确定了该顶点的距离,导致其无法处理具有负边的图。与之相对地, DAG 最短路算法中,通过「入度」信息, 确保了任意顶点一定能够穷尽所有入边的松弛 ,因此可以适用于有负边的图 (DAG) ,但为了确保入度能减至 0 ,要求图不能有圈。我们自然会想,有没有什么办法能够结合二者的优点,使得最短路算法能够同时处理有圈且有负边的图呢?答案是肯定的,只要我们通过某种方式,在不借助入度的情况下保证所有顶点都能够执行其所有入边的松弛,就可以实现上述要求。本节介绍的 Bellman-Ford 算法就是具有这样特点的最短路算法。
本节中我会给出叙述式的 Bellman-Ford 算法正确性证明 (说明),并展示其「动态规划」的本质。为了能够更好地理解算法过程,在「实例说明」中展示算法运行的详细过程。在「负边图 & 负圈图」一节中说明该算法能够处理负边图以及不能够处理负圈图的原因。
在「代码」中,我们仍旧通过 743. 网络延迟时间 一题来展示 Bellman-Ford 的写法。
Bellman-Ford 在1950年代中后期被多个学者独立发明,以至于在算法冠名权上有些争议。Jeff Erickson 在他的 Algorithms 一书的 8.7 节开头,做了如下介绍。
The simplest implementation of Ford’s generic shortest-path algorithm was first sketched by Alfonso Shimbel in 1954, described in more detail by Edward Moore in 1957, and independently rediscovered by Max Woodbury and George Dantzig in 1957, by Richard Bellman in 1958, and by George Minty in 1958. (Neither Woodbury and Dantzig nor Minty published their algorithms.) In full compliance with Stigler’s Law, the algorithm is almost universally known as Bellman-Ford , because Bellman explicitly used Ford’s 1956 formulation of relaxing edges, although some authors refer to “Bellman-Kalaba” and a few early sources refer to “Bellman-Shimbel”.
于是 Jeff Erickson 干脆十分公允地写道:
The Shimbel / Moore / Woodbury-Dantzig / Bellman-Ford / Kalaba / Minty / Brosh algorithm can be summarized in one line:
Bellman-Ford: Relax ALL the tense edges, then recurse.
算法描述
Bellman-Ford Algorithm(贝尔曼-福特算法) : 与 Dijkstra 算法的相同点是对边 (或者说对顶点) 不断执行松弛操作 ,以逐渐得到所有顶点到源点的最短距离。Dijkstra 每次循环「贪心地」完成 一个 顶点最短路径的确定,而 BF 算法则对图的 所有边 ( ∣ E ∣ |E| ∣ E ∣ ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 全量松弛操作 ,第 i i i i + 1 i+1 i + 1 ∣ V ∣ |V| ∣ V ∣ s s s
※ 实际上任何最短路算法都无法求出「负圈图」的最短路,因为通过在负圈上不断绕圈,路径长度可以无限小,也就是 负圈上的顶点不存在「最短路」 。后面我们将看到,虽无法给出负圈图的最短路结果 (因为本来就没有),但 BF 算法能够判断图是否存在负圈 。
※ 作者看过一些资料称全量松弛次数为 ∣ V ∣ |V| ∣ V ∣ ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
算法过程
建图及初始化。
构建带权图。
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] s s s I n f i n i t y Infinity I n f ini t y s s s
设置一个 f i n i s h e d finished f ini s h e d
置 s s s
外层循环执行 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 「松弛所有边」 。
进入外层循环后按顶点顺序依次对所有顶点 u u u v v v d u + ∣ ( u , v ) ∣ < d v du + |(u, v)| < dv d u + ∣ ( u , v ) ∣ < d v d v = d u + ∣ ( u , v ) ∣ dv = du + |(u, v)| d v = d u + ∣ ( u , v ) ∣ f i n i s h e d = f a l s e finished = false f ini s h e d = f a l se v v v u u u
在一次「松弛所有边」的操作中,若没有任何边被松弛,表明所有可能的松弛已完成 (负圈图除外), 此时可 「提前」退出最外层循环 。
外层循环结束时,(若无负圈) 每个顶点到源点的最短路径距离被求出。
检查图是否有负圈。再次对所有边执行松弛操作, 若有边可被松弛,则有负圈 ,结束程序,否则正常结束,所有顶点最短路径被求出。
正确性证明 (说明)
已知若一个顶点 v v v 最后一次松弛 后,必有 d v = δ v dv=δv d v = δ v d v dv d v v v v δ v δv δ v v v v
易知,第 i i i i i i 必被松弛 。例如第 1 次全量松弛,s s s s s s
∣ e d g e s ( s , v ) ∣ |edges(s, v)| ∣ e d g es ( s , v ) ∣ s s s v v v ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 s s s v v v ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 v v v i i i i i i
由此,v v v s s s v v v max { ∣ e d g e s ( s , v ) ∣ , v ∈ V } \max\{|edges(s, v)|, v ∈ V\} max { ∣ e d g es ( s , v ) ∣ , v ∈ V } max { ∣ e d g e s ( s , v ) ∣ , v ∈ V } ≤ ∣ V ∣ − 1 \max\{|edges(s, v)|, v ∈ V\} ≤ |V|-1 max { ∣ e d g es ( s , v ) ∣ , v ∈ V } ≤ ∣ V ∣ − 1 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 图的所有入边必定都松弛过且完成了所有可能的松弛 (某条入边属于多个层次时,可能经过多次松弛) 。如果把图看成以 s s s 树的高度 。对某一顶点,可以说该顶点至多经过其 最大深度减 1 次 全量松弛后取得最短路径。
上述过程对任意顶点均成立,故 BF 算法正确性得证。
此证明也可以看作如下「动态规划」过程。为单串 O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 )
定义: d p [ j ] dp[j] d p [ j ] s s s j j j
边界: d p [ s ] = 0 dp[s] = 0 d p [ s ] = 0
递推: d p [ j ] = d p [ j − 1 ] + ∣ ( j − 1 , j ) ∣ dp[j] = dp[j - 1] + |(j - 1, j)| d p [ j ] = d p [ j − 1 ] + ∣ ( j − 1 , j ) ∣ j − 1 j - 1 j − 1 s − j s-j s − j
根据前述,j − 1 j - 1 j − 1 j j j d p [ j − 1 ] dp[j - 1] d p [ j − 1 ] d p [ j ] dp[j] d p [ j ]
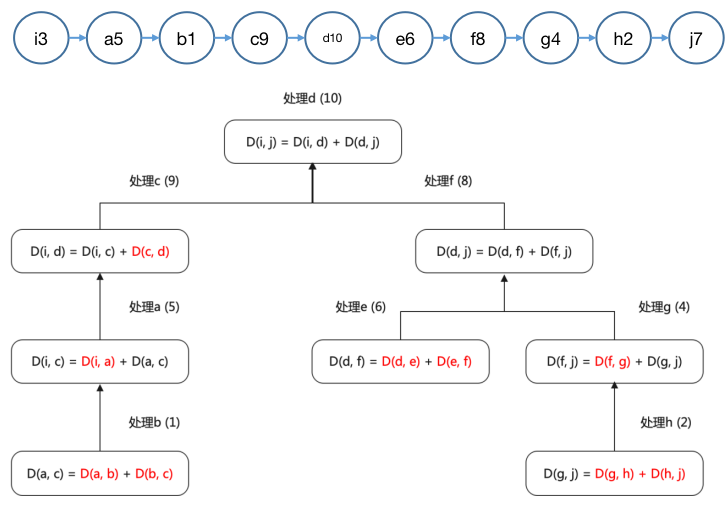
实例说明
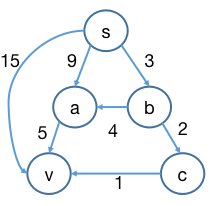
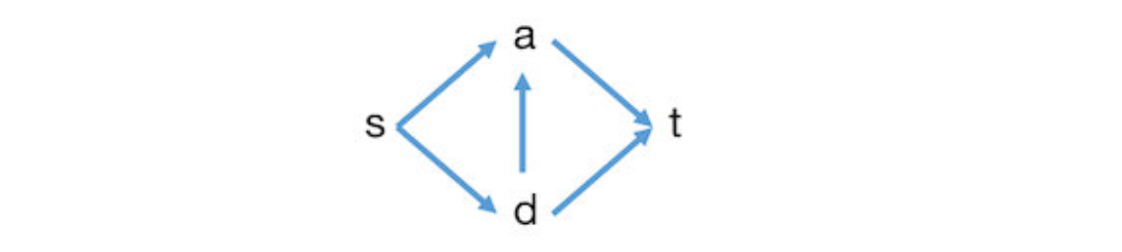
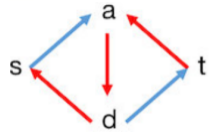
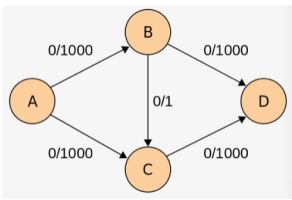
以下实际考察 BF 算法对下图的求解过程,重点关注顶点 v v v 这里 )
p ( s , v ) p(s, v) p ( s , v )
p 1 : s > v , ∣ p 1 ∣ = 15 p1: s > v ,|p1| = 15 p 1 : s > v , ∣ p 1∣ = 15 ( s , v ) (s, v) ( s , v ) v v v
p 2 : s > a > v , ∣ p 2 ∣ = 14 p2: s > a > v,|p2| = 14 p 2 : s > a > v , ∣ p 2∣ = 14 ( a , v ) (a, v) ( a , v ) v v v
p 3 : s > b > a > v , ∣ p 3 ∣ = 12 p3: s > b > a > v ,|p3| = 12 p 3 : s > b > a > v , ∣ p 3∣ = 12 ( a , v ) (a, v) ( a , v ) v v v
p 4 : s > b > c > v , ∣ p 4 ∣ = 6 p4: s > b > c > v ,|p4| = 6 p 4 : s > b > c > v , ∣ p 4∣ = 6 ( c , v ) (c, v) ( c , v ) v v v
可以看到 ( a , v ) (a, v) ( a , v ) v v v p 3 p3 p 3 p 4 p4 p 4 v v v s , a , c , b , v s, a, c, b, v s , a , c , b , v
松弛过程
d s ds d s d a da d a d c dc d c d b db d b d v dv d v
初始
0 (*) ∞
∞
∞
∞
第1次全量松弛
0
∞ > 9 ∞
∞ > 3 (*) ∞ > 15
第2次全量松弛
0
9 > 7 (*) ∞ > 5 (*) 3
15 > 14
第3次全量松弛
0
7
5
3
14 > 12 > 6 (*)
1 2 3 4 5 6 7 8 备注: 1. 初始时令 ds 为0,(*)表示已取得该顶点最短路径。 2. 第1次。(s, a), (s,b), (s, v)属于第1层入边,被松弛。 且b只有一条入边,即经过这趟松弛操作,使得 db = δb。 3. 第2次。第1层入边不会再被松弛。第2层入边(a, v), (b, a), (b, c)被松弛。 经过这趟松弛操作,a, c的全部入边松弛完毕,使得 da = δa,dc = δc。 4. 第3次。第1,2层入边不会再被松弛,第3层入边(a, v), (c, v)被松弛。 v 的全部入边松弛完毕,使得 dv = δv。
负边图 & 负圈图
负边图。由于该算法在 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1
负圈图。当图存在负圈时,s s s ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
提前结束优化
当某一次全量松弛过程中没有边被松弛,说明所有可能的松弛已被穷尽,可提前结束程序。
最坏情形
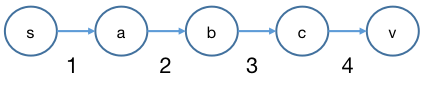
当图中存在两点间路径长度为 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 s > a > b > c > v s > a > b > c > v s > a > b > c > v ∣ ( s , a ) ∣ = 1 |(s, a)| = 1 ∣ ( s , a ) ∣ = 1 ∣ ( a , b ) ∣ = 2 |(a, b)| = 2 ∣ ( a , b ) ∣ = 2 ∣ ( b , c ) ∣ = 3 |(b, c)| = 3 ∣ ( b , c ) ∣ = 3 ∣ ( c , v ) ∣ = 4 |(c, v)| = 4 ∣ ( c , v ) ∣ = 4 这里 )
时空复杂度
时间复杂度:每次全量松弛要操作 ∣ E ∣ |E| ∣ E ∣ ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 O ( ( ∣ V ∣ − 1 ) ∣ E ∣ ) O((|V|-1)|E|) O (( ∣ V ∣ − 1 ) ∣ E ∣ ) O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ )
空间复杂度:存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) d i s t s dists d i s t s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
如下是 743. 网络延迟时间 的 Bellman-Ford 解法。代码中设置了 f i n i s h e d finished f ini s h e d f o r for f or
此代码是 Bellman-Ford 算法的较为普遍的写法 (提前结束优化 + 负圈检测),读者应熟练掌握。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution { public int networkDelayTime (int [][] times, int n, int k) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; boolean finished = true ; for (int i = 0 ; i < n - 1 ; i++) { for (int u = 0 ; u < n; u++) { for (int [] v_weight : graph.get(u)){ int v = v_weight[0 ], weight = v_weight[1 ]; long dv = (long ) dists[u] + (long ) weight; if (dv < dists[v]) { dists[v] = (int ) dv; finished = false ; } } } if (finished) break ; else finished = true ; } for (int u = 0 ; u < n; u++) { for (int [] v_weight : graph.get(u)){ int v = v_weight[0 ], weight = v_weight[1 ]; long dv = (long ) dists[u] + (long ) weight; if (dv < dists[v]) { System.out.println("Negtive Cycle Found!" ); } } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } }
SPFA (BFM)
学习 Bellman-Ford 时我们隐隐感觉到「全量松弛」做了许多无意义的松弛尝试,自然地,我们想能否优化松弛次数,在保证穷尽顶点所有入边松弛这一前提下,尽量少地松弛呢?或者干脆说,我们希望所有的松弛,都是有效松弛,也就是顶点所有入边的松弛是无遗漏且不重复的。本节中,我们将看到 SPFA (BFM) 算法在 BF 的基础上是如何借助队列轻松地实现这一改进的。
BFM 即 Bellman-Ford-Moore,这一改进由 Edward F. Moore 他于1959 年发表的 The shortest path through a maze 关于最短路径的SPFA快速算法 的论文,重新提出了Moore的改进 ,并且给了个比较通俗的名字 Shortest Path Fast Algorithm。
算法描述
SPFA算法(最短路径快速算法) :SPFA 算法是对 BF 算法的一种改进。在BF 算法的说明中我们指出,第 i i i i + 1 i+1 i + 1 b f s bfs b f s i + 1 i+1 i + 1 b f s bfs b f s q q q i i i i + 1 i+1 i + 1 i + 1 i+1 i + 1 ∣ V ∣ |V| ∣ V ∣
我们还可以这样看,一个顶点 v v v 前提 :v v v u u u d u + ∣ ( u , v ) ∣ < d v du + |(u, v)| < dv d u + ∣ ( u , v ) ∣ < d v d v dv d v ∣ ( u , v ) ∣ |(u, v)| ∣ ( u , v ) ∣ d u du d u d v dv d v d u du d u d v dv d v u u u v v v v v v v v v q q q s s s w h i l e while w hi l e q q q u u u u u u v v v d v dv d v 有机会被更新 ,所以将 v v v v v v 需要注意的是 ,v v v v v v O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ ) 否则这一复杂度将无法得到保证 。重复上述过程,当 q q q 无法再触发其邻接顶点距离的更新 。也可以说对任意一个顶点 u u u s s s u u u d u du d u
算法过程
建图及初始化。
构建带权图。
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] s s s I n f i n i t y Infinity I n f ini t y s s s
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ i n C o u n t s [ ] inCounts[] in C o u n t s [ ]
设置一个队列 q q q
置 s s s
s s s
通过 w h i l e ( ! q . i s E m p t y ( ) ) while(!q.isEmpty()) w hi l e ( ! q . i s E m pt y ( )) u u u u u u 尝试松弛其所有邻边 。
对顶点 u u u v v v d u + ∣ ( u , v ) ∣ < d v du + |(u, v)| < dv d u + ∣ ( u , v ) ∣ < d v d v = d u + ∣ ( u , v ) ∣ dv = du + |(u, v)| d v = d u + ∣ ( u , v ) ∣ inCounts[v] > |V| - 1 ,若满足,说明存在负圈,可直接结束程序,否则 inCounts[v]++ 。若需要求完整路径,可在松弛的同时更新 v v v u u u
w h i l e while w hi l e
正确性证明 (说明)
SPFA 算法与 BF 算法的核心内容都在于 穷尽所有路径带来的所有可能的松弛 。BF 算法通过 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 i i i 有效松弛 仅作用于第 i + 1 i+1 i + 1 通过队列来减少松弛的次数 。第 i i i i i i ∣ V ∣ |V| ∣ V ∣
实例说明
仍以前一张网络图为例考察 SPFA 算法的求解过程,进一步看清其正确性及 SPFA 与 BF 的关系。
第 1 层顶点只有 s s s s s s a , b , v a,b,v a , b , v v , a , c v,a,c v , a , c
松弛过程
d s ds d s d a da d a d c dc d c d b db d b d v dv d v 队列 q q q
1. 初始
0 (*) ∞
∞
∞
∞
s;
2. s出
0
∞ > 9 ∞
∞ > 3 (*) ∞ > 15 a, b, v ;
3. a出
0
9
∞
3
15 > 14 b, v;
4. b出
0
9 > 7 (*) ∞ > 5 (*) 3
14
v; a, c
5. v出
0
7
5
3
14
a, c;
6. a出
0
7
5
3
14 > 12 c; v
7. c出
0
7
5
3
12 > 6 (*) v;
8. v出
0
7
5
3
14
空
1 2 3 4 5 6 7 8 9 10 11 1. 初始时令 ds 为0,(*)表示已取得该顶点最短路径。「;」是层的分隔符。 2. s 出队时松弛 (s, a), (s,b), (s, v)。 且 b 只有一条路径,即经过这趟松弛操作,使得 db = δb。 3. a 出队时松弛 (a, v),这是 v 的距离第 2 次被松弛。 4. b 出队时松弛 (b, a), (b, c),a 有两条路径,c 只有一条, 于是 da = δa,dc = δc。 5. 无可松弛边。 6. a 出队时松弛 (a, v),这是 v 的距离第 3 次被松弛。 7. c 出队时松弛 (c, v),这是 v 的距离第 4 次被松弛。 此时 p(s, v) 所有可能的路径带来的 v 的入边的松弛均已完成,于是 dv = δv 。 8. 无可松弛边,队列空,程序结束。
负边图 & 负圈图
负圈判定: 记录每个顶点入队的次数,顶点 v v v ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1
当图只有一个节点时,要小心处理负圈检测。如下伪代码,次数检测写在次数加一之前可以 避免单节点图被误判为负圈 。
1 2 3 4 5 6 7 if(!q.contains(w)) { // 检查w是否已经在q中 q.add(w) // 将w加入队列 if(w.inCount > |V| - 1) { // 若大于|V|-1则检出负圈 System.err.println("存在负圈!") } else w.inCount++ // 记录入队次数 }
当然也可以调换次数检测和加一的顺序,并把 > ∣ V ∣ − 1 > |V| - 1 > ∣ V ∣ − 1 > ∣ V ∣ > |V| > ∣ V ∣
1 2 3 4 5 6 7 if(!q.contains(w)) { // 检查w是否已经在q中 q.add(w) // 将w加入队列 w.inCount++ // 记录入队次数 if(w.inCount > |V|) { // 若大于|V|则检出负圈 System.err.println("存在负圈!") } }
Bellman-Ford-Moore 和 SPFA
本节开头我们已经说过,SPFA 实际上应当称作 Bellman-Ford-Moore 算法。根据Wiki词条 Bellman-Ford algorithm 的介绍,「对所有的边,简单地松弛 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
1 2 3 1955年 Alfonso Shimbel 1956年 Lester Ford Jr. 1958年 Richard Bellman
又过了一年,1959年的时候 Edward F. Moore 提出了 BF 算法的一个改进 ,即前文的伪代码 (SPFA / Bellman-Ford-Moore) 。
A variation of the Bellman-Ford algorithm known as Shortest Path Faster Algorithm , first described by Moore (1959) , reduces the number of relaxation steps that need to be performed within each iteration of the algorithm.
1994年,西南交通大学的段凡丁在该年4月的《西南交通大学学报》里发表了题为《关于最短路径的SPFA快速算法 》的论文,重新提出了Moore的改进 ,并且给了个比较通俗的名字 Shortest Path Fast Algorithm。段老师显然没看过 Moore 当初的论文,否则不会给出一个错误的复杂度估计(给出的复杂度是 O ( k ∣ E ∣ ) O(k|E|) O ( k ∣ E ∣ )
时空复杂度
时间复杂度:O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ )
1 2 3 4 5 6 7 8 9 10 SPFA (Bellman-Ford-Moore) 算法伪代码: 1 Queue q 2 q.add(s) // s的距离初始为0, 其他顶点的距离初始为Infinity 3 while(!q.isEmpty()) 4 v = q.remove() 5 for (w : v.adjs) // w是v的邻接顶点 6 if(dv + d(v, w) < dw) 7 dw = dv + d(v, w) 8 if(!q.contains(w)) //检查w是否在当前队列中,不在则入队 9 q.add(w)
按层分析很容易得到 SPFA 的复杂度。顶点一层一层地入队出队,一张图最多有 ∣ V ∣ |V| ∣ V ∣ s s s 按层计 ,任何顶点最多只能入队 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 s > a > c , s > b > c s > a > c,s > b > c s > a > c , s > b > c c c c 一个顶点最多只能在一层顶点里出现一次 。考虑每层顶点个数小于 ∣ V ∣ |V| ∣ V ∣ ∣ E ∣ |E| ∣ E ∣ O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ )
第 8 行 if(!q.contains(w)) 是SPFA 作为改进 BF 的关键,有必要继续进一步说明为何加了这个检查优化 不影响结果的正确性 。假设从 s s s v v v v v v v v v w w w w w w v v v v v v
SPFA 每出队第 i i i i + 1 i+1 i + 1 i i i i i i i + 1 i+1 i + 1 if(dv + |(v, w)| < dw) 询问了一次。于是,SPFA 便实现了对顶点的 「无遗漏且不重复」 的松弛这一改进。
空间复杂度:存图空间 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) d i s t s / i n C o u n t s / q dists/inCounts/q d i s t s / in C o u n t s / q O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
对时间复杂度的分析可以看出,稀疏图中顶点 v v v p ( s , v ) p(s, v) p ( s , v )
代码
如下是 743. 网络延迟时间 的 SPFA(BFM) 解法。代码中应用了「负圈检测」,由于本题已保证了不存在负值边,也就不存在负圈,因此负圈检测可以省略。
此代码是 SPFA 算法的较为普遍的写法 (带负圈检测),读者应熟练掌握。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution { public int networkDelayTime (int [][] times, int n, int k) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : times){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); } int max = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n], inCounts = new int [n]; Arrays.fill(dists, INF); dists[k - 1 ] = 0 ; Queue<Integer> q = new ArrayDeque <>(); q.add(k - 1 ); while (!q.isEmpty()){ int u = q.remove(); for (int [] v_weight : graph.get(u)){ int v = v_weight[0 ], weight = v_weight[1 ]; int dv = dists[u] + weight; if (dv < dists[v]){ dists[v] = dv; if (!q.contains(v)) { q.add(v); if (inCounts[v] > n - 1 ) { System.out.println("Negtive Cycle Found!" ); return -1 ; } else inCounts[v]++; } } } } for (int dist : dists){ if (dist == INF) return -1 ; if (dist > max) max = dist; } return max; } }
带权全源最短路
在「带权单源最短路」中,我们介绍了 Dijkstra / DAG SSSP (归为特殊 Dijkstra) / Bellman-Ford / SPFA (BFM) 最短路算法。若想求图上任意两点的距离,在这些算法中将不得不一个个计算,我们不禁会想,有没有什么算法可以一次求解所有顶点对 (all pairs) 的最短路径呢?本节我们介绍的就是这样一种一次性求解所有点对最短距离的算 Floyd-Warshall 算法。
Jeff Erickson 在他的 Algorithms 一书的 9.8 节开头,介绍了 Floyd-Warshall 算法被多人相继独立发明 (发现) 的历史。
…A difffferent formulation of shortest paths that removes this logarithmic factor was proposed twice in 1962, first by Robert Floyd and later independently by Peter Ingerman, both slightly generalizing an algorithm of Stephen Warshall published earlier in the same year. In fact, Warshall’s algorithm was previously discovered by Bernard Roy in 1959, and the underlying recursion pattern was used by Stephen Kleene in 1951.
除了展示 Floyd-Warshall 算法可用于解决求单源最短路的 743. 网络延迟时间 一题,我们还会展示更适合用它来求解的全源最短路问题 1334. 阈值距离内邻居最少的城市 。
Floyd-Warshall
Floyd-Warshall算法(弗洛伊德算法) : 求解图中任意两点的最短路径的算法。算法以 3 重循环考察任意顶点 i i i j j j k k k k k k d ( i , k ) + d ( k , j ) < d ( i , j ) d(i, k) + d(k, j) < d(i, j) d ( i , k ) + d ( k , j ) < d ( i , j ) d ( i , j ) = d ( i , k ) + d ( k , j ) d(i, j) = d(i, k) + d(k, j) d ( i , j ) = d ( i , k ) + d ( k , j )
可以这样理解其工作过程。已知确定的任意两点 i , j i, j i , j p ( i , j ) p(i, j) p ( i , j ) I n f i n i t y Infinity I n f ini t y p ( i , j ) p(i, j) p ( i , j ) p ( i , j ) p(i, j) p ( i , j ) y y y p ( i , j ) = p ( i , y ) + p ( y , j ) p(i, j) = p(i, y) + p(y, j) p ( i , j ) = p ( i , y ) + p ( y , j ) p ( i , y ) p(i, y) p ( i , y ) p ( y , j ) p(y, j) p ( y , j ) p ( i , j ) p(i, j) p ( i , j ) x x x p ( i , y ) p(i, y) p ( i , y ) p ( i , y ) = p ( i , x ) + p ( x , y ) p(i, y) = p(i, x) + p(x, y) p ( i , y ) = p ( i , x ) + p ( x , y ) z z z p ( y , j ) p(y, j) p ( y , j ) p ( y , j ) = p ( y , z ) + p ( z , j ) p(y, j) = p(y, z) + p(z, j) p ( y , j ) = p ( y , z ) + p ( z , j ) p ( i , j ) p(i, j) p ( i , j ) p ( i , j ) p(i, j) p ( i , j ) i > a > b i > a > b i > a > b a a a i i i b b b i > a > b i > a > b i > a > b 「连接起来」 (因为 最短路径上的任意子路径都是最短的 ,必松弛)。顺着算法执行过程不难看出,算法通过外循环的 k k k
在「正确性证明 (说明)」中我们将进一步透过「动态规划」来把握该算法正确性。
算法过程
建图及初始化。
构建带权图。在 Floyd-Warshall 算法中,以「邻接矩阵」构建带权图是更方便也更普遍的做法。
设置一个大小为 ∣ V ∣ ∗ ∣ V ∣ |V|*|V| ∣ V ∣ ∗ ∣ V ∣ d i s t s [ ] [ ] dists[][] d i s t s [ ] [ ] I n f i n i t y Infinity I n f ini t y ∣ V ∣ ∗ ∣ V ∣ |V|*|V| ∣ V ∣ ∗ ∣ V ∣
外层循环执行 ∣ V ∣ |V| ∣ V ∣ k k k
中层循环执行 ∣ V ∣ |V| ∣ V ∣ i i i
内层循环执行 ∣ V ∣ |V| ∣ V ∣ j j j
考察是否有 d ( i , k ) + d ( k , j ) < d ( i , j ) d(i, k) + d(k, j) < d(i, j) d ( i , k ) + d ( k , j ) < d ( i , j ) d ( i , j ) = d ( i , k ) + d ( k , j ) d(i, j) = d(i, k) + d(k, j) d ( i , j ) = d ( i , k ) + d ( k , j )
外层循环结束时,(若无负圈) 所有顶点对的最短路径距离被求出。
检查图是否有负圈。再次对所有边执行松弛操作, 若有边可被松弛,则有负圈 ,结束程序,否则正常结束,所有顶点最短路径被求出。
※ 以下展示如何通过路径信息的矩阵 p p p
p [ i ] [ j ] p[i] [j] p [ i ] [ j ] k k k i i i k k k j j j k k k i > a > b > c > j i > a > b > c > j i > a > b > c > j
顶点
i i i a a a b b b c c c j j j
i i i n u l l null n u ll n u l l null n u ll a a a n u l l null n u ll b b b
a a a n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll
b b b n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll c c c
c c c n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll
j j j n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll n u l l null n u ll
利用该矩阵,通过递归即可找到 i > a > b > c > j i > a > b > c > j i > a > b > c > j
1 2 3 4 5 6 7 8 i > j, 找到b i > b,找到a i > a为null,输出i a > b为null,输出a b > j,找到c b > c为null,输出b c > j为null,输出c 最后输出j
正确性证明 (说明)
该算法的 本质是动态规划 ,以状态转移方程的形式描述如下,其中 d p [ k ] [ i ] [ j ] dp[k][i][j] d p [ k ] [ i ] [ j ] 经过前 k k k i i i j j j 。注意第一维的 k k k k k k
1 2 3 1. 定义: dp[k][i][j] 表示经过前 k 个顶点的松弛,得到的顶点 i 到顶点 j 的最短路径长度。 2. 边界: dp[0][i][j] = Infinity 3. 递推: dp[k][i][j] = min{dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j]}
最短路径 不经过 第 k k k k k k d p [ k ] [ i ] [ j ] = d p [ k − 1 ] [ i ] [ j ] dp[k][i][j] = dp[k-1][i][j] d p [ k ] [ i ] [ j ] = d p [ k − 1 ] [ i ] [ j ]
最短路径 经过 第 k k k k k k d p [ k ] [ i ] [ j ] = d p [ k − 1 ] [ i ] [ k ] + d p [ k − 1 ] [ k ] [ j ] dp[k][i][j] = dp[k-1][i][k] + dp[k-1][k][j] d p [ k ] [ i ] [ j ] = d p [ k − 1 ] [ i ] [ k ] + d p [ k − 1 ] [ k ] [ j ]
1 2 3 4 5 6 for (k : V) for (i : V) for (j : V) if (d(i, k) + d(k, j) < d(i, j)) d(i, j) = d(i, k) + d(k, j)
补充说明:已知点 i , j i, j i , j p ( i , j ) p(i, j) p ( i , j ) p ( i , j ) p(i, j) p ( i , j ) a , c a, c a , c p ( i , j ) p(i, j) p ( i , j ) p ( i , j ) p(i, j) p ( i , j ) a , c a, c a , c p ( i , j ) p(i, j) p ( i , j ) b b b i , j i, j i , j p ( i , j ) p(i, j) p ( i , j ) p ( i , a ) + p ( a , b ) + p ( b , c ) + p ( c , j ) p(i, a) + p(a, b) + p(b, c)+ p(c, j) p ( i , a ) + p ( a , b ) + p ( b , c ) + p ( c , j )
实例分析
下面通过一个例子观察 Floyd 算法的动态规划过程,对其正确性可以有更直观的感受。由于算法总是在整张图上进行处理,展示整张图将使过程变得杂乱,因此我们只选取一条 i i i j j j 任意两点 的路径的构成都是类似的。
设图 G G G i , j i, j i , j p p p i > a > b > c > d > e > f > g > h > j i > a > b > c > d > e > f > g > h > j i > a > b > c > d > e > f > g > h > j b , h , i , g , a , e , j , f , c , d b, h, i, g, a, e, j, f, c, d b , h , i , g , a , e , j , f , c , d d d d d ( i , j ) d(i, j) d ( i , j ) p p p p p p i i i j j j
外层循环处理 d d d d ( i , d ) + d ( d , j ) d(i, d) + d(d, j) d ( i , d ) + d ( d , j ) i i i j j j d ( i , j ) d(i, j) d ( i , j ) d ( i , d ) d(i, d) d ( i , d ) d ( d , j ) d(d, j) d ( d , j ) d ( i , d ) d(i, d) d ( i , d ) d ( d , j ) d(d, j) d ( d , j ) d d d c c c c c c d ( i , d ) = d ( i , c ) + d ( c , d ) d(i, d) = d(i, c) + d(c, d) d ( i , d ) = d ( i , c ) + d ( c , d ) d ( c , d ) d(c, d) d ( c , d ) d ( i , c ) d(i, c) d ( i , c ) d ( i , c ) = d ( i , a ) + d ( a , c ) d(i, c) = d(i, a) + d(a, c) d ( i , c ) = d ( i , a ) + d ( a , c ) d ( i , a ) d(i, a) d ( i , a ) d ( a , c ) = d ( a , b ) + d ( b , c ) d(a, c) = d(a, b) + d(b, c) d ( a , c ) = d ( a , b ) + d ( b , c ) d ( a , b ) d(a, b) d ( a , b ) d ( b , c ) d(b, c) d ( b , c )
可以看出,外层循环处理 i 到 j 的最短路径的所有顶点的过程中,先处理的顶点得到 子路径总能够为后处理的顶点构建更长的子路径 ,直到处理 (最短路径上的) 最后一个顶点时,将两个子路径连接起来形成最终的最短路径,这正是动态规划过程的体现。
不同于 BF 动态规划过程的单串 O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) 不一定直接作用于下一次松弛 ,而是在之后某一次松弛中发生作用。例如处理 b ( 1 ) b(1) b ( 1 ) h ( 2 ) h(2) h ( 2 ) a > b > c a>b>c a > b > c g > h > j g>h>j g > h > j a ( 5 ) a(5) a ( 5 ) a > b > c a>b>c a > b > c i > a > b > c i>a>b>c i > a > b > c c ( 9 ) c(9) c ( 9 ) i > a > b > c > d i>a>b>c>d i > a > b > c > d g > h > j g>h>j g > h > j g ( 4 ) g(4) g ( 4 ) f > g > h > j f>g>h>j f > g > h > j f ( 8 ) f(8) f ( 8 ) d > e > f > g > h > j d>e>f>g>h>j d > e > f > g > h > j d > e > f d>e>f d > e > f e ( 6 ) e(6) e ( 6 ) d ( 10 ) d(10) d ( 10 ) i > a > b > c > d > e > f > g > h > j i > a > b > c > d > e > f > g > h > j i > a > b > c > d > e > f > g > h > j
总结 Floyd 算法的过程,外层循环执行完第 k k k k + 1 k+1 k + 1 1 , 2 , . . . , k + 1 1, 2, ... , k+1 1 , 2 , ... , k + 1 k + 2 k+2 k + 2
负边图 & 负圈图
时空复杂度
时间复杂度: 3 重循环,O ( ∣ V ∣ 3 ) O(|V|^3) O ( ∣ V ∣ 3 )
空间复杂度: 邻接矩阵、距离矩阵、路径信息矩阵 (若有的话) 均为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
代码
如下是 743. 网络延迟时间 的 Floyd-Warshall 解法。代码中应用了「负圈检测」,由于本题已保证了不存在负值边,也就不存在负圈,因此负圈检测可以省略。另外,此实现采用了 「邻接矩阵」 存图。
此代码是 Floyd-Warshall 算法的较为普遍的写法 (带负圈检测),读者应熟练掌握。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution { public int networkDelayTime (int [][] times, int n, int k) { int [][] dists = new int [n][n]; int max = 0 , INF = Integer.MAX_VALUE; for (int [] distRow : dists) Arrays.fill(distRow, INF); for (int u = 0 ; u < n; u++) dists[u][u] = 0 ; for (int i = 0 ; i < times.length; i++){ int u = times[i][0 ] - 1 , v = times[i][1 ] - 1 , weight = times[i][2 ]; dists[u][v] = weight; } for (int k1 = 0 ; k1 < n; k1++) { for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++){ long ik = dists[i][k1], kj = dists[k1][j], ij = dists[i][j]; if (ik + kj < ij) { dists[i][j] = (int ) (ik + kj); } } } } for (int dist : dists[k - 1 ]){ if (dist == INF) return -1 ; if (dist > max) max = dist; } for (int u = 0 ; u < n; u++) { for (int v = 0 ; v < n; v++){ long dv = (long ) dists[k - 1 ][u] + (long ) dists[u][v]; if (dv < dists[k - 1 ][v]) { System.out.println("Negtive Cycle Found!" ); } } } return max; } }
现在,我们展示 Floyd-Warshall 解决 1334. 阈值距离内邻居最少的城市 一题的代码如下。该题是典型的「所有点对」最短距离问题。求解过程十分简单。
应用 Floyd-Warshall 算法求出所有点对间最短距离,存于矩阵 d i s t s [ ] [ ] dists[][] d i s t s [ ] [ ]
遍历 d i s t s dists d i s t s
因为 u u u
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public int findTheCity (int n, int [][] edges, int distanceThreshold) { int INF = Integer.MAX_VALUE; int [][] dists = new int [n][n]; for (int [] distRow : dists) Arrays.fill(distRow, INF); for (int u = 0 ; u < n; u++) dists[u][u] = 0 ; for (int [] edge : edges){ int u = edge[0 ], v = edge[1 ], weight = edge[2 ]; dists[u][v] = weight; dists[v][u] = weight; } for (int k = 0 ; k < n; k++){ for (int i = 0 ; i < n; i++){ for (int j = 0 ; j < n; j++){ long ik = dists[i][k], kj = dists[k][j], ij = ik + kj; if (ij < dists[i][j]){ dists[i][j] = (int ) ij; } } } } int ans = 0 , minCount = n; for (int u = 0 ; u < n; u++){ int count = 0 ; for (int v = 0 ; v < n; v++){ if (dists[u][v] <= distanceThreshold) count++; } if (count <= minCount) { minCount = count; ans = u; } } return ans; } }
小结
总结「最短路径」算法如下。
算法
时间复杂度
负边
正圈
负圈
无权 SSSP
● 朴素版
O ( V 2 ) O(V^2) O ( V 2 ) -
Yes
-
● 队列版
O ( V + E ) O(V+E) O ( V + E ) -
Yes
-
带权 SSSP
● Dijkstra 朴素版
O ( V 2 ) O(V^2) O ( V 2 ) No
Yes
No(不可检测)
● Dijkstra 小顶堆版
O ( E l o g V ) O(ElogV) O ( El o g V ) No
Yes
No(不可检测)
● Dijkstra DAG
O ( V + E ) O(V+E) O ( V + E ) Yes
No (可检测)
No (可检测)
● Bellman-Ford
O ( V E ) O(VE) O ( V E ) Yes
Yes
No (可检测)
● SPFA (BFM)
O ( V E ) O(VE) O ( V E ) Yes
Yes
No (可检测)
带权 APSP
●Floyd-Warshall
O ( V 3 ) O(V^3) O ( V 3 ) Yes
Yes
No (可检测)
※ 本文未涉及「无权 APSP」,无权图的所有点对最短路可通过对所有顶点执行无权单源最短路算法求得,时间复杂度为 O ( ( ∣ V ∣ + ∣ E ∣ ) ∗ ∣ V ∣ ) O((|V|+|E|)*|V|) O (( ∣ V ∣ + ∣ E ∣ ) ∗ ∣ V ∣ ) All pairs shortest path in undirected and unweighted graphs 。
※ 空间复杂度主要取决于建图方式,以「邻接矩阵」建图时为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
最小生成树
在最短路径问题中,研究的是如何找到图中两点的最短路径,当我们将整张图作为对象考虑时,很自然地会想,在图上所有顶点都互相连通的基础上,如何找到最小的总路径和呢?这有点像是 以图为整体的「最短路径」 。很容易找到这个问题的现实意义,例如给一个科技园区铺装光纤,要求所有办公楼和厂房都互相连通且尽可能节省光纤用量。办公楼和厂房为图中顶点,互相之间的距离为边权,该场景实际上是要求找到能将所有顶点连通且边权和最小的边集。这个边集就是本节要介绍的 「最小生成树」 。
最小生成树 ( Minimum Spanning Tree, MST ) : 通常指的无向图中的一个边集,该边集使得图中所有顶点互相连通,且边权总和最小。由于此边集构成的子图必然无圈,该子图为一棵树,因此称该边集为「最小生成树」。
本节讲解求图上 MST 的两种算法: Prim 和 Kruskal,我们将看到前者几乎和 Dijkstra 一致,而后者只是并查集思想的简单应用。同样,为了在学习这两个算法过程中及时得到反馈,我们将以 1135. 最低成本联通所有城市 一题作为配套,有了 Dijkstra 和并查集的基础,MST 的学习是十分轻松的。
Prim
Prim 算法与 Dijkstra 算法无论是从思想还是实际代码表现上都非常类似,在理解了 Dijkstra 的基础上,学习 Prim 几乎没有思考成本。后续我们以一个表格逐行比较二者的内容,读者将发现 二者最根本的差别只在于顶点距离的更新方法 。由于有了 Dijkstra 的基础,行文中,我们着重对比二者,对 Prim 算法只做必要的简略讲解。我们仍循前例,先介绍「朴素版」再介绍「优先队列版」。读者务必在阅读本节之前还阅读 Dijkstra 章节。
与之前的几个算法类似,Prim算法也曾被多人在不同时间相继独立发明 (发现) 。Jeff Erickson 在他的 Algorithms 一书的 7.4 节开头,做了如下介绍。
The next oldest minimum spanning tree algorithm (Prim’s algorithm) was first described by the Czech mathematician Vojtěch Jarník in a 1929 letter to Borůvka; Jarník published his discovery the following year. The algorithm was independently rediscovered by Joseph Kruskal in 1956, (arguably) by Robert Prim in 1957, by Harry Loberman and Arnold Weinberger in 1957, and finally by Edsger Dijkstra in 1958. Prim, Lobermand and Weinberger, and Dijkstra all (eventually) knew of and even cited Kruskal’s paper, but since Kruskal also described two other minimum spanning-tree algorithms in the same paper, this algorithm is usually called “Prim’s algorithm”, or sometimes “the Prim/Dijkstra algorithm”, even though by 1958 Dijkstra already had another algorithm (inappropriately) named after him.
Jeff Erickson 在他的书中几乎只将此算法称为 Jarník 算法,不过本文还是按照流行的说法称为 Prim 算法。
朴素版
算法描述
Prim (普里姆算法) : 一种基于贪心思想的求解无向图上 MST 的算法。我们直接将 Prim 算法和 Dijkstra 二者对比如下。
Dijkstra
Prim
贪心算法
贪心算法
顶点分为 距离已确定 和 距离未确定 顶点
顶点分为 距离已确定 (已加入生成树) 和 距离未确定 (未加入生成树) 顶点
所有顶点距离初始化为 I n f i n i t y Infinity I n f ini t y
所有顶点距离初始化为 I n f i n i t y Infinity I n f ini t y
源点 s s s
生成树起始点 s s s
以一个循环寻找 当前距离未确定顶点中距离最小者 u u u u u u
以一个循环寻找 当前距离未确定顶点中距离最小者 u u u u u u
尝试以如下方式更新 (松弛) u u u d v = m i n ( d v , d u + d ( u , v ) ) dv = min(dv, du + d(u, v)) d v = min ( d v , d u + d ( u , v ))
尝试以如下方式更新 u u u d v = m i n ( d v , d ( u , v ) ) dv = min(dv, d(u,v)) d v = min ( d v , d ( u , v ))
w h i l e while w hi l e w h i l e while w hi l e
我们看到这两个算法的每一步都几乎相同,不同点主要有三处,最主要的是第 3 点。
Prim 用于在「无向图」中求 MST,因此建图时要「双向建边」。Dijkstra 应用于有向图时单向建边,应用于无向图时双向建边。
Dijkstra 中的「距离」指的是顶点到源点的距离。Prim 中的「距离」指的是顶点到其已在生成树上的邻接顶点 (父顶点) 的距离。
顶点距离更新方式不同 。
算法过程
建图及初始化。
构建双向带权图。
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ b o o l e a n boolean b oo l e an v i s i t e d [ ] visited[] v i s i t e d [ ]
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] I n f i n i t y Infinity I n f ini t y
任意选取 一个顶点作为起始顶点,置距离为 0,通常我们将第一个顶点的距离置为 0 。
以一个循环寻找 当前距离未确定顶点中距离最小者 u u u u u u
距离更新。尝试更新 u u u 距离未确定的 邻接顶点 v v v d v dv d v d v = m i n { d v , ∣ ( u , v ) ∣ } dv = min\{dv, |(u,v)|\} d v = min { d v , ∣ ( u , v ) ∣ }
循环结束时,所有顶点距离被求出,也就是 MST 所有边权被求出。
正确性证明
如下证明参考了 参考1 以及 参考2 。
虽然 Prim 算法过程与 Dijkstra 类似,但证明过程并不通用。如下是 Prim 算法的证明过程。
证明:在图 G G G S S S
记 G G G S m i n S_{min} S min ∣ S ∣ = ∣ S m i n ∣ |S| = |S_{min}| ∣ S ∣ = ∣ S min ∣
在 S S S 首次 遇到的不属于 S m i n S_{min} S min e = ( u , v ) e=(u, v) e = ( u , v ) u u u v v v S S S e e e S S S u u u U U U v v v V V V
S m i n S_{min} S min u u u v v v u u u U U U v v v V V V ( u , v ) ∉ S m i n (u,v)∉S_{min} ( u , v ) ∈ / S min f = ( a , b ) ∈ S m i n f=(a,b)∈S_{min} f = ( a , b ) ∈ S min U → V U → V U → V a a a U U U b b b V V V a a a u u u b b b v v v b b b v v v a a a u u u
当 e e e S S S a a a U U U U U U S S S
此时 a a a a a a U U U g g g a a a e e e S S S 首次 遇到的不属于 S m i n S_{min} S min g ∈ S m i n g∈S_{min} g ∈ S min f ∈ S m i n f∈S_{min} f ∈ S min a a a a a a f f f S m i n S_{min} S min
由于 a a a u u u a a a e e e S S S f f f ∣ e ∣ ≤ ∣ f ∣ |e|≤|f| ∣ e ∣ ≤ ∣ f ∣
对于 S m i n S_{min} S min f = ( a , b ) f=(a,b) f = ( a , b ) S m i n S_{min} S min A A A B B B u → a → b → v u → a → b → v u → a → b → v u u u v v v A , B A, B A , B e = ( u , v ) e=(u,v) e = ( u , v ) S A e B S_{AeB} S A e B ∣ e ∣ ≤ ∣ f ∣ |e|≤|f| ∣ e ∣ ≤ ∣ f ∣ ∣ e ∣ = ∣ f ∣ |e|=|f| ∣ e ∣ = ∣ f ∣ S A e B S_{AeB} S A e B S m i n S_{min} S min ∣ S A e B ∣ = ∣ S m i n ∣ |S_{AeB}|=|S_{min}| ∣ S A e B ∣ = ∣ S min ∣ S A e B S_{AeB} S A e B
重复上述过程,继续考察 S S S S m i n S_{min} S min S S S ∣ S ∣ = ∣ S m i n ∣ |S|=|S_{min}| ∣ S ∣ = ∣ S min ∣ S S S
时空复杂度
与朴素版 Dijkstra 算法相同,不赘述。
时间复杂度:O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 )
空间复杂度:O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
1135. 最低成本联通所有城市 一题是非常典型的求 MST 的题目,应用本节的朴素 Prim 解法轻松可解,而且你会发现,只需对 743. 网络延迟时间 的朴素 Dijkstra 解法做几行修改即可得到此代码。求解时需要注意以下两点。
构建带权图时要双向建边。
当存在距离未更新的顶点时说明图不连通时,返回 -1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { public int minimumCost (int n, int [][] connections) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : connections){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); graph.get(v).add(new int []{u, weight}); } int sum = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; boolean [] visited = new boolean [n]; Arrays.fill(dists, INF); dists[0 ] = 0 ; int u = -1 ; while ((u = getMin(dists, visited)) != -1 ) { visited[u] = true ; for (int [] v_weight : graph.get(u)) { int v = v_weight[0 ], weight = v_weight[1 ]; if (!visited[v]) { if (weight < dists[v]) { dists[v] = weight; } } } } for (int dist : dists){ if (dist == INF) return -1 ; sum += dist; } return sum; } private int getMin (int [] dists, boolean [] visited) { int n = dists.length, min = Integer.MAX_VALUE, minVertex = -1 ; for (int u = 0 ; u < n; u++) { if (!visited[u] && dists[u] < min) { min = dists[u]; minVertex = u; } } return minVertex; } }
优先队列版
算法描述
与 Dijkstra 一样,Prim 也可用优先队列 (小顶堆) 优化,内容一致,不赘述。
算法过程
建图及初始化。
构建双向带权图。
设置一个小顶堆 p q pq pq
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ b o o l e a n boolean b oo l e an v i s i t e d [ ] visited[] v i s i t e d [ ]
设置一个大小为 ∣ V ∣ |V| ∣ V ∣ d i s t s [ ] dists[] d i s t s [ ] I n f i n i t y Infinity I n f ini t y
置任意一个顶点的距离为 0,通常我们将第一个顶点的距离置为 0 。
上述顶点入堆。
一次出堆完成一个顶点距离的确定,即将该顶点加入 MST。以 w h i l e while w hi l e p q pq pq u u u u u u u u u
更新操作。尝试更新 u u u 距离未确定的 邻接顶点 v v v d v dv d v d v = m i n { d v , ∣ ( u , v ) ∣ } dv = min\{dv, |(u,v)|\} d v = min { d v , ∣ ( u , v ) ∣ }
循环结束时,所有顶点距离被求出,也就是 MST 所有边权被求出。
时空复杂度
与优先队列版 Dijkstra 算法相同,不赘述。
时间复杂度:O ( ∣ E ∣ l o g ∣ V ∣ ) O(|E|log|V|) O ( ∣ E ∣ l o g ∣ V ∣ )
空间复杂度:O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
同样地,当图为 「稠密图」 时,采用更优的「朴素版」;当图为 「稀疏图」 时,采用更优的「优先队列版」。
代码
现在,我们给出如下利用优先队列的 Prim 算法代码来解决 1135. 最低成本联通所有城市 。同样地,只需对 743. 网络延迟时间 的优先队列版 Dijkstra 解法做几行修改即可得到此代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public int minimumCost (int n, int [][] connections) { List<List<int []>> graph = new ArrayList <>(); for (int i = 0 ; i < n; i++) graph.add(new ArrayList <>()); for (int [] edge : connections){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; graph.get(u).add(new int []{v, weight}); graph.get(v).add(new int []{u, weight}); } int sum = 0 , INF = Integer.MAX_VALUE; int [] dists = new int [n]; boolean [] visited = new boolean [n]; Arrays.fill(dists, INF); dists[0 ] = 0 ; PriorityQueue<int []> pq = new PriorityQueue <>((u, v) -> u[1 ] - v[1 ]); pq.add(new int []{0 , 0 }); while (!pq.isEmpty()) { int [] u_dist = pq.remove(); int u = u_dist[0 ]; if (visited[u]) continue ; visited[u] = true ; for (int [] v_weight : graph.get(u)) { int v = v_weight[0 ], weight = v_weight[1 ]; if (!visited[v]) { if (weight < dists[v]) { dists[v] = weight; pq.add(new int []{v, weight}); } } } } for (int dist : dists){ if (dist == INF) return -1 ; sum += dist; } return sum; } }
Kruskal
前述 Prim 算法从一个顶点出发,逐渐「长出」一棵 MST,而本节的 Kruskal 算法在「生成」MST 的过程上与 Prim 颇有相对之感,该方法令 MST 的各部分各自生长,最终合并成一棵完整的 MST。Kruskal 算法是并查集的典型应用,需要读者先了解并查集。在之前的「初探图搜索 (遍历)」 - 「无向图连通性」 - 「并查集」中我已提过,我在另一篇文章中对并查集做过较为全面的介绍,如果读者还不熟悉并查集,那么在开始本节之前,可以先阅读我写的 并查集从入门到出门 (全文1w+ 字,尝试透彻分析并查集的基本内容,2022 年 5 月中旬在力扣讨论区发布后两周内收获 5k 阅读量,500+ 收藏,100+ 点赞及大量好评)。
后续内容在假设你已了解了「并查集」基本内容的基础上,均只做非常简要的说明 (因为详细内容都已在「并查集从入门到出门」中呈现)。
Joseph B. Kruskal 于 1956 年发表的 论文 中描述了该算法。
算法描述
Kruskal (克鲁斯卡尔算法) : 一种基于贪心思想的求解无向图上 MST 的算法。该算法首先将所有边按边权排序,接着应用「并查集」的「查询-合并」过程来决定将哪些边加入到 MST 中。算法内容的简要描述为: 对排序后的边权,依序 (按边权从小到大) 取边 ( u , v ) (u,v) ( u , v ) u , v u, v u , v ( u , v ) (u,v) ( u , v ) ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
算法过程
构建双向带权图。
按边权从小到大排序所有边。
实现以顶点的并查集。
从排序后的边中依序 (按边权从小到大) 选取边 ( u , v ) (u, v) ( u , v )
当加入的边数等于 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
若依序取完所有的边后,加入 MST 的边数仍达不到 ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1
时空复杂度
时间复杂度: 边权排序 O ( ∣ E ∣ l o g ∣ E ∣ ) O(|E|log|E|) O ( ∣ E ∣ l o g ∣ E ∣ ) O ( α ( n ) ) O(\alpha(n)) O ( α ( n )) O ( 1 ) O(1) O ( 1 ) ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 O ( ∣ V ∣ + ∣ E ∣ l o g ∣ E ∣ ) O(|V|+|E|log|E|) O ( ∣ V ∣ + ∣ E ∣ l o g ∣ E ∣ ) O ( ∣ E ∣ l o g ∣ V ∣ ) O(|E|log|V|) O ( ∣ E ∣ l o g ∣ V ∣ )
空间复杂度: 建图 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) p a r e n t s / r a n k parents / rank p a re n t s / r ank O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
现在,我们给出如下利用 Kruskal 算法代码来解决 1135. 最低成本联通所有城市 。并查集采用「带路径压缩的查找 + 按秩合并」的组合。熟悉「并查集」之后我们能够非常轻松地写出该代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { public int minimumCost (int n, int [][] connections) { Arrays.sort(connections, (a, b) -> a[2 ] - b[2 ]); int sum = 0 , count = 0 ; int [] parents = new int [n]; for (int i = 0 ; i < n; i++) parents[i] = i; UnionFind uf = new UnionFind (parents); for (int [] edge : connections){ int u = edge[0 ] - 1 , v = edge[1 ] - 1 , weight = edge[2 ]; if (uf.find(u) != uf.find(v)){ uf.union(u, v); sum += weight; count++; if (count == n - 1 ) return sum; } } return -1 ; } } class UnionFind { int [] parents, rank; public UnionFind (int [] parents) { this .parents = parents; this .rank = new int [parents.length]; Arrays.fill(rank, 1 ); } public int find (int x) { if (parents[x] == x) return x; return parents[x] = find(parents[x]); } public void union (int x, int y) { int xRoot = find(x), yRoot = find(y); if (xRoot != yRoot){ if (rank[yRoot] <= rank[xRoot]){ parents[yRoot] = xRoot; } else parents[xRoot] = yRoot; if (rank[xRoot] == rank[yRoot]) rank[xRoot]++; } } }
小结
本节介绍了两种常见的求解「最小生成树」的算法,在掌握 Dijkstra 算法的基础上,Prim 只需简单对照学习即可完全掌握。对于 Kruskal,仅仅是并查集的典型应用,因此在掌握了并查集的基础上,学习 Kruskal 也是十分轻松的。
「最短路径」算法中,由于最短路是边权的累计,在无法穷尽松弛的算法中,例如 Dijkstra,我们特别强调了其无法处理负边图的特点,且所有的最短路径算法都不能求解负圈图 (有的可以检测出负圈) 。但「最小生成树」比较边权的大小而无「累计」效应,因此 负边和负圈都不影响算法的正确性 ,也就是在讨论「最小生成树」时,我们 无需考虑图是否有圈以及是否有负边 。
网络流
图论中,除了关心顶点到顶点的「最短距离」和整张图的「最小生成树」之外,人们还关心 顶点间的「流量」 。将图想象成一张信息网络,信息在顶点之间流动,每条边的权值限制了同一时间承载流量的上限,我们想知道,从一个顶点到另一个顶点,一次最多能够发送多少流量,这就是同样著名的「最大流」问题。在本节中我们将从著名的 「最大流最小割定理」 的证明开始,深入讨论该问题,并给出几种求最大流的算法。
最大流最小割定理
最大流最小割定理(Max-flow min-cut theorem) :对于一张网络图 G G G s s s t t t 最大流量等于最小割所有割边容量之和 。
以下将从 路径存在问题 引入 割和割的大小 的概念,再由割的大小与 s − t s-t s − t
定理证明过程整理自B站南大老师蒋炎岩的授课视频: [算法竞赛入门] 网络流基础: 理解最大流/最小割定理 ,同时也增加了作者的理解。
在这里我们提前指出 Ford-Fulkerson 方法的正确性证明与最大流最小割定理的证明等价 ,这意味着它们会被 同时证明 。如下,也就是 k = m k = m k = m k = l k = l k = l
Ford-Fulkerson方法的正确性证明:图 G G G s − t s-t s − t k k k m m m k = m k=m k = m
最大流最小割定理证明:图 G G G s − t s-t s − t k k k s − t s-t s − t l l l k = l k=l k = l
L. R. Ford Jr. & D. R. Fulkerson (1962) Flows in Networks , 这一 论文 第23页,作者给出的最大流最小割定理描述如下。
Theorem 5.1 Max flow min cut theorem.
For any network the maximal flow value from s s s t t t s s s t t t
从路径存在问题到割
s − t s-t s − t s − t s-t s − t 路径 存在。对于路径存在问题,通常以 D F S / B F S DFS/BFS D FS / BFS s s s t t t s − t s-t s − t s − t s-t s − t s , a , b , c , d , t s, a, b ,c, d, t s , a , b , c , d , t
1 2 3 4 5 6 7 s > t s > a > t s > b > t ... s > a > b > t s > a > c > t ...
对于上述列表中的一条路径,若该路径中的每对相邻顶点构成的边均存在,则该路径为一条 s − t s-t s − t s − t s-t s − t
对于路径存在问题,罗列所有可能路径并逐一判断的方法虽最严格,但显然不是证明的好办法。再次考虑 D F S / B F S DFS/BFS D FS / BFS s s s S S S s s s T T T s − t s-t s − t 等价于 S S S T T T ,由此引入如下 割 的概念。
割的定义 :割 (cut) 是图 G G G 顶点集 V V V 。有向图 G ( V , E ) G(V, E) G ( V , E ) s − t s-t s − t C = ( S , T ) C = (S, T) C = ( S , T ) V V V S S S T T T s ∈ S s ∈ S s ∈ S t ∈ T t ∈ T t ∈ T
割的大小 :对于上述割,其大小指从 S S S T T T ( u , v ) ∈ E ∣ u ∈ S , v ∈ T (u, v) ∈ E | u ∈ S, v ∈ T ( u , v ) ∈ E ∣ u ∈ S , v ∈ T 割边 。
根据割及其大小的定义,只要存在 s − t s-t s − t V V V s − t s-t s − t S S S T T T s − t s-t s − t s , a , d , e , h ∈ S , b , c , f , g , i , t ∈ T s, a, d, e, h ∈ S, b, c, f, g, i, t ∈ T s , a , d , e , h ∈ S , b , c , f , g , i , t ∈ T s − t s-t s − t s ∈ S s ∈ S s ∈ S s s s t ∈ T t ∈ T t ∈ T t t t s − t s-t s − t 若 s − t s-t s − t s − t s-t s − t 。
因此,要想证明 s − t s-t s − t 只需要找到一个大小为 0 的 s − t s-t s − t 。 注意,当 s − t s-t s − t s − t s-t s − t s − t s-t s − t s − t s-t s − t
不相交路径数量与割的大小
现在,我们初步建立了「流」与「割」在特定情形下的联系,即上述分析给出的「s − t s-t s − t s − t s-t s − t s − t s-t s − t s − t s-t s − t 不相交的 s − t s-t s − t 数量 (再次注意,我们当前讨论的是无权图,「数量」即「流量」)。s − t s-t s − t 不相交 路径指对于多条 s − t s-t s − t 没有公共边 。后续我们通过如下三个量的关系来证明定理,即证明 k = l k = l k = l
k k k 实际存在的 s − t s-t s − t
m m m 算法找到的 s − t s-t s − t
l l l 最小 s − t s-t s − t
不相交路径数上界
假设图有 k k k s − t s-t s − t k k k k ( k = 0 , k = 1 , k = 2 , . . . ) k (k = 0, k = 1, k = 2,...) k ( k = 0 , k = 1 , k = 2 , ... ) k = 0 k=0 k = 0 s − t s-t s − t s − t s-t s − t k = 0 k=0 k = 0 k > 0 k > 0 k > 0 s − t s-t s − t
下图 k = 1 k=1 k = 1 s − t s-t s − t 不相交路径数量受到割边 ( b , c ) (b, c) ( b , c ) ,如果所有 s − t s-t s − t s − t s-t s − t s − t s-t s − t 不相交 路径至多为 1。若最小割大小为 2,则存在 2 条经过 2 条不同割边的 s − t s-t s − t s − t s-t s − t c c c s − t s-t s − t k k k k ≤ c k ≤ c k ≤ c c = l c = l c = l k ≤ l k≤l k ≤ l s − t s-t s − t c c c k k k 上界 ,l l l k k k 最紧上界 。现在我们离目标近了一步,即「割边数」c c c s − t s-t s − t k k k k ≤ c k ≤ c k ≤ c k ≤ l k≤l k ≤ l
不相交路径数下界
上述以割边数给出了不相交路径数量 k k k m m m m m m k k k m = l m = l m = l k = l k = l k = l D F S / B F S DFS/BFS D FS / BFS m m m G G G s − t s-t s − t p p p k = 0 k=0 k = 0 不相交 的,需要从 G G G p p p k = k + 1 k = k + 1 k = k + 1 s > d > a > t s > d > a > t s > d > a > t k = 2 k=2 k = 2 s > a > t , s > d > t s > a > t, s > d > t s > a > t , s > d > t D F S / B F S DFS/BFS D FS / BFS m m m k k k m = k m = k m = k
反向边 (路径)
L. R. Ford, JR & D. R. Fulkerson 在1956年的论文 中修正了单纯以 D F S / B F S DFS/BFS D FS / BFS t − s t-s t − s s − t s-t s − t 添加原路径的反向路径 ,仅此而已。如前图,找到 s > d > a > t s > d > a > t s > d > a > t t > a > d > s t > a > d > s t > a > d > s s − t s-t s − t s > a > d > t s > a > d > t s > a > d > t s − t s-t s − t m = 2 m=2 m = 2
s − t s-t s − t 增广路径(Augmenting Path) ,可以将反向路径称作 反向增广路径 。添加这一反向路径的操作是整个算法最为核心的部分,以下证明这一操作的正确性,即以「寻找增广路-删除该路径-添加反向路径」这一FF方法得到 m m m s − t s-t s − t m = k m = k m = k k = l k = l k = l m = k m=k m = k
证明k=m
蒋岩炎老师的视频中不以严谨的数学证明,而是以图形化的直观方式证明了最大流最小割定理 (也即证明了 FF 方法的正确性)。
添加反向边的有效性
如下左图 (图中的 s s s t t t p 1 , p 2 , p 3 p1, p2, p3 p 1 , p 2 , p 3 D F S / B F S DFS/BFS D FS / BFS s − t s-t s − t p 4 p4 p 4 p 4 p4 p 4 p 1 , p 2 , p 3 p1, p2, p3 p 1 , p 2 , p 3 原边 ,另一种是与 p 2 p2 p 2 p 3 p3 p 3 p 2 p2 p 2 p 3 p3 p 3 反向边 ,它们使得 p 4 p4 p 4 t t t s − t s-t s − t m = 4 m = 4 m = 4
p 4 p4 p 4 原图 中确实有 4 条不相交路径。为了看出这一点,找到 p 4 p4 p 4 p 4 p4 p 4 p 4 p4 p 4 p 1 , p 2 , p 3 p1, p2, p3 p 1 , p 2 , p 3 p 1 p1 p 1 p ′ 2 , p ′ 3 , p ′ 4 p'2, p'3, p'4 p ′ 2 , p ′ 3 , p ′ 4 原图 中的 s − t s-t s − t p ′ 2 , p ′ 3 , p ′ 4 p'2, p'3, p'4 p ′ 2 , p ′ 3 , p ′ 4 p 2 , p 3 p2, p3 p 2 , p 3 p 4 p4 p 4
尽管算法找到的路径与下右图显示的原图上的路径不同,但数量是正确的 。如果还有 p 5 p5 p 5 在示意图中那些通过反向边得到的 (在原图中不存在的) 路径看起来就像是切开了起初得到的路径 (p 2 , p 3 p2, p3 p 2 , p 3 s s s t t t 。
k的确定与最小割的大小
上述内容说明了添加反向边能够找到新的 (在不添加反向边时可能找不到的) 不相交路径,并且我们看到算法找到的路径与原图实际的路径 一一对应 (数量相等) 。有了这些准备工作,我们开始证明 k = m k = m k = m
已经知道 m = 4 m = 4 m = 4 k ≥ m = 4 k ≥ m = 4 k ≥ m = 4
如果找到原图 G G G s − t s-t s − t C C C l = 4 l = 4 l = 4
对于 2,指出一个割,直接证明它是 「最小的」 是困难的,因此我们不必考虑它是不是最小,转而考虑在原图中寻找一个大小 c = 4 c=4 c = 4 C C C m ≤ k ≤ c m≤k≤c m ≤ k ≤ c m = k = c = 4 m=k=c=4 m = k = c = 4 k = 4 k=4 k = 4 m = k = l = c = 4 m=k=l=c=4 m = k = l = c = 4
上述 3 就意味着 FF 方法 (m = k m=k m = k k = l k=l k = l
根据这个思路,我们接着前图继续分析。再次强调,现在的目标是 在原图中寻找一个大小为 c = 4 c=4 c = 4 C C C 。
以上中图为例,将 p 4 p4 p 4 G f ′ G_{f'} G f ′
残留图 G f ′ G_{f'} G f ′ ,一种是 s − t s-t s − t s − t s-t s − t p 1 , p ′ 2 , p ′ 3 , p ′ 4 p1, p'2, p'3, p'4 p 1 , p ′ 2 , p ′ 3 , p ′ 4 s − t s-t s − t t − s t-s t − s s − t s-t s − t s − t s-t s − t s − t s-t s − t C C C C C C
割 C C C G f ′ G_{f'} G f ′ s s s S S S T T T
该割大小为 0 ,反证法简单可证明。若有割边,也就是还能从 S S S v v v T T T u u u s s s v v v u u u G f ′ G_{f'} G f ′ s s s S S S u u u t t t G f ′ G_{f'} G f ′ s − t s-t s − t
推论: 割 C C C G G G
证明如下:
割 C C C G f ′ G_{f'} G f ′ S S S T T T
残留图与原图的区别仅仅是 不相交路径的方向相反 。
在原图 G G G S S S s − t s-t s − t s − t s-t s − t T T T 贡献且仅贡献了 4 条割边 。
也就是说每条 s − t s-t s − t s − t s-t s − t S − T S-T S − T
因为原图 G G G s − t s-t s − t G f ′ G_{f'} G f ′ t − s t-s t − s s − t s-t s − t S − T S-T S − T t − s t-s t − s T − S T-S T − S C C C
假设在残留图 G f ′ G_{f'} G f ′ t − s t-s t − s T − S T-S T − S 路径是连续的 ,穿越过程必然是 T → S → T → S T→S→T→S T → S → T → S S − T S-T S − T 这与残留图 G f ′ G_{f'} G f ′ s − t s-t s − t ( G f ′ G_{f'} G f ′ C C C
因此原图 G G G s − t s-t s − t S − T S-T S − T C C C G G G
推论得证。
至此,通过找到残留图 G f ′ G_{f'} G f ′ C C C C C C
我们在指出原图 G f G_f G f C C C m = c = 4 m = c = 4 m = c = 4 m ≤ k ≤ c m≤k≤c m ≤ k ≤ c k = m = 4 k = m = 4 k = m = 4 k = 4 k=4 k = 4 s − t s-t s − t C C C 割 C C C ,综上,有 m = k = l = c = 4 m=k=l=c=4 m = k = l = c = 4
m = k m=k m = k k = l k = l k = l
推广至有权图
只需将边权为 n n n n n n s > a > t s > a > t s > a > t ( s , a ) (s, a) ( s , a ) ( a , t ) (a, t) ( a , t )
Ford-Fulkerson
在「最大流最小割定理及其证明」中我们已经介绍了 Ford-Fulkerson 方法并证明了该方法的正确性。本节我们继续讲解该方法更详细的内容。
算法描述
Ford-Fulkerson方法(福特-富尔克森方法) : 1956 年 L. R. Ford Jr 和 D. R. Fulkerson 在其发表的 论文 中描述的基于 贪心思想 的求 有向图最大流 的算法。因为该算法未指定求增广路径的具体算法,所以通常将其称作 Ford-Fulkerson 方法 (Method) 而非 Ford-Fulkerson 算法 (Algorithm) 。若增广路径 以 b f s bfs b f s ,则为 Edmonds-Karp 算法 。此外也可以以 d f s dfs df s 结合 b f s bfs b f s d f s dfs df s 。FF 首先设置要求解的目标,即源点 s s s t t t f f f s − t s-t s − t p 1 p1 p 1 p 1 p1 p 1 s s s p 1 p1 p 1 t t t c ( p 1 ) c(p1) c ( p 1 ) f f f s s s t t t c ( p 1 ) c(p1) c ( p 1 ) t t t s s s s s s t t t s − t s-t s − t f f f s − t s-t s − t
算法过程
给定一张图 G ( V , E ) G(V, E) G ( V , E ) s s s t t t G G G s s s t t t f f f
设置一张残留网络 (残留图/残差图/残余图,residual graph ) G f Gf G f G f Gf G f G G G
考察 G f Gf G f s s s t t t p p p p p p ( u , v ) ∈ p (u,v) ∈ p ( u , v ) ∈ p c ( u , v ) > 0 c(u, v) > 0 c ( u , v ) > 0 p p p 增广路径 (Augmenting Path) 。若存在 p p p p p p 最小边的权 c c c f f f p p p c c c p p p c c c
在 G f Gf G f p p p G f Gf G f p p p f f f s s s t t t
※ 虽然根据 wiki 的说法 Ford-Fulkerson 未指定求增广路的具体方式,但若以 d f s dfs df s
算法正确性证明
请参考「最大流最小割定理」。
两种坏情形
小边权增广路径情形
如下图,寻找从 A A A B B B A > B > C > D A>B>C>D A > B > C > D A > C > B > D A>C>B>D A > C > B > D C > B C>B C > B B , C B,C B , C A > B > D A>B>D A > B > D A > C > D A>C>D A > C > D
以 b f s bfs b f s
算法无法终止的情形
算法能够结束的隐含前提是 每次找到的增广路至少使 s s s t t t ,只要最大流是固定的,经过有限次操作后总能发送到最大流。如果边权存在 无理数 ,则算法可能无法结束。以下举例说明 (该例来自 Wiki )。
如下图的流量网络,e 1 = ( b , a ) , e 2 = ( d , c ) , e 3 = ( b , c ) e1 = (b, a), e2 = (d, c), e3 = (b, c) e 1 = ( b , a ) , e 2 = ( d , c ) , e 3 = ( b , c ) ∣ e 1 ∣ = ∣ e 3 ∣ = 1 |e1| = |e3| = 1 ∣ e 1∣ = ∣ e 3∣ = 1 ∣ e 2 ∣ = r = ( √ 5 − 1 ) / 2 |e2| = r = (√5 - 1) / 2 ∣ e 2∣ = r = ( √5 − 1 ) /2 M ( M > = 2 ) M (M >= 2) M ( M >= 2 ) r 2 = 1 − r r^2 = 1 - r r 2 = 1 − r r 3 = r − r 2 r^3 = r - r^2 r 3 = r − r 2 r 4 = r 2 − r 3 r^4 = r^2 - r^3 r 4 = r 2 − r 3 p 0 = s > b > c > t p0 = s > b > c > t p 0 = s > b > c > t p 1 = s > d > c > b > a > t p1 = s > d > c > b > a > t p 1 = s > d > c > b > a > t p 2 = s > b > c > d > t p2 = s > b > c > d > t p 2 = s > b > c > d > t p 3 = s > a > b > c > t p3 = s > a > b > c > t p 3 = s > a > b > c > t p 0 , p 1 , p 2 , p 1 , p 3 , p 1 , p 2 , p 1 , p 3 , p 1 , p 2 , p 1 , p 3... p0, p1, p2, p1, p3, p1, p2, p1, p3, p1, p2, p1, p3... p 0 , p 1 , p 2 , p 1 , p 3 , p 1 , p 2 , p 1 , p 3 , p 1 , p 2 , p 1 , p 3...
观察下表经过上述顺序一次循环后的结果,步骤 1 和步骤 5 时 e 1 , e 2 , e 3 e1, e2, e3 e 1 , e 2 , e 3 r n , r n + 1 , 0 r^n, r^{n+1}, 0 r n , r n + 1 , 0 1 + 2 ( r 1 + r 2 ) 1+2(r^1+r^2) 1 + 2 ( r 1 + r 2 ) e 1 , e 2 , e 3 e1, e2, e3 e 1 , e 2 , e 3 r n , r n + 1 , 0 r^n, r^{n+1}, 0 r n , r n + 1 , 0 1 + 2 ∑ r i 1+2∑r^i 1 + 2 ∑ r i r r r
1 + 2 ∑ r i = 1 + 2 ∗ r / ( 1 − r ) 1+2∑r^i = 1 + 2*r/(1-r)
1 + 2 ∑ r i = 1 + 2 ∗ r / ( 1 − r )
将 r = 1 − r 2 = ( 1 + r ) ∗ ( 1 − r ) r = 1 - r^2 = (1+r)*(1-r) r = 1 − r 2 = ( 1 + r ) ∗ ( 1 − r ) r r r 3 + 2 r 3+2r 3 + 2 r 2 + √ 5 2+√5 2 + √5 2 M + 1 > 5 > 2 + √ 5 2M + 1 > 5 > 2+√5 2 M + 1 > 5 > 2 + √5
步骤
增广路
发送流
e1剩余
e2剩余
e3剩余
0
r 0 = 1 r^0 = 1 r 0 = 1 r 1 r^1 r 1 1
1
p 0 p0 p 0 1
r 0 r^0 r 0 r 1 r^1 r 1 0
2
p 1 p1 p 1 r r r r 2 r^2 r 2 0
r 1 r^1 r 1
3
p 2 p2 p 2 r r r r 2 r^2 r 2 r 1 r^1 r 1 0
4
p 1 p1 p 1 r 2 r^2 r 2 0
r 3 r^3 r 3 r 2 r^2 r 2
5
p 3 p3 p 3 r 2 r^2 r 2 r 2 r^2 r 2 r 3 r^3 r 3 0
时空复杂度
时间复杂度:O ( ∣ E ∣ ∗ f ) O(|E|*f) O ( ∣ E ∣ ∗ f )
设最大流为 f f f O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) b f s / d f s bfs/dfs b f s / df s O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( ∣ E ∣ ∗ f ) O(|E|*f) O ( ∣ E ∣ ∗ f ) f f f b f s bfs b f s O ( ∣ V ∣ ∣ E ∣ 2 ) O(|V||E|^2) O ( ∣ V ∣∣ E ∣ 2 ) b f s bfs b f s d f s dfs df s O ( ∣ V ∣ 2 ∣ E ∣ ) O(|V|^2|E|) O ( ∣ V ∣ 2 ∣ E ∣ )
空间复杂度:依赖于存图及求最短路径的具体方法,采用邻接表存图,则存图空间为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) b f s bfs b f s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) d f s dfs df s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
代码
我们采用 d f s dfs df s
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 package com.yukiyama.demo;import java.util.*;import java.io.*;public class FF { boolean [] visited; int [] ends, heads, nexts, weights, preEdges, pre, saturatedWeights; int edgeNum; public static void main (String[] args) { Scanner cin = new Scanner (System.in); int n = cin.nextInt(), m = cin.nextInt(), s = cin.nextInt() - 1 , t = cin.nextInt() - 1 ; FF demo = new FF (); demo.visited = new boolean [n]; demo.ends = new int [2 * m + 2 ]; demo.nexts = new int [2 * m + 2 ]; demo.weights = new int [2 * m + 2 ]; demo.preEdges = new int [n]; demo.heads = new int [n]; demo.pre = new int [n]; demo.saturatedWeights = new int [n]; demo.edgeNum = 1 ; demo.init(m, cin); cin.close(); System.out.println(demo.ek(s, t)); } public long ek (int s, int t) { if (s == t) return 0 ; long max = 0 , incFlow = 0 ; while ((incFlow = dfs(s, t, Integer.MAX_VALUE)) > 0 ) { max += incFlow; Arrays.fill(visited, false ); } return max; } private void init (int m, Scanner cin) { for (int i = 0 ; i < m; i++) { int u = cin.nextInt() - 1 , v = cin.nextInt() - 1 , weight = cin.nextInt(); ++edgeNum; ends[edgeNum] = v; weights[edgeNum] = weight; nexts[edgeNum] = heads[u]; heads[u] = edgeNum; ++edgeNum; ends[edgeNum] = u; weights[edgeNum] = 0 ; nexts[edgeNum] = heads[v]; heads[v] = edgeNum; } } private long dfs (int u, int t, long incFlow) { if (u == t) return incFlow; visited[u] = true ; for (int edgeNo = heads[u]; edgeNo != 0 ; edgeNo = nexts[edgeNo]) { int v = ends[edgeNo], weight = weights[edgeNo]; if (visited[v] || weight == 0 ) continue ; long saturatedWeight = 0 ; if ((saturatedWeight = dfs(v, t, Math.min(incFlow, weight))) > 0 ) { weights[edgeNo] -= saturatedWeight; weights[edgeNo ^ 1 ] += saturatedWeight; return saturatedWeight; } } return 0 ; } }
Edmonds-Karp
算法描述
Edmonds-Karp算法 (埃德蒙兹-卡普算法) : 以 b f s bfs b f s s − t s-t s − t t − s t-s t − s s s s t t t
算法过程
给定一张图 G ( V , E ) G(V, E) G ( V , E ) s s s t t t G G G s s s t t t f f f
设置一张残留网络 (残留图/残差图/残余图,residual graph ) G f Gf G f G f Gf G f G G G
以 b f s bfs b f s 考察 G f Gf G f s s s t t t p p p p p p ( u , v ) ∈ p (u,v) ∈ p ( u , v ) ∈ p c ( u , v ) > 0 c(u, v) > 0 c ( u , v ) > 0 p p p 增广路径 (Augmenting Path) 。若存在 p p p p p p 最小边的权 c c c f f f p p p c c c p p p c c c
在 G f Gf G f p p p G f Gf G f p p p f f f s s s t t t
时空复杂度
以下证明 EK 算法的时间复杂度为:O ( ∣ V ∣ ∣ E ∣ 2 ) O(|V||E|^2) O ( ∣ V ∣∣ E ∣ 2 )
本证明参考了证明1 、证明2 。
1. 一次BFS增广
每次 b f s bfs b f s < 2 ∣ E ∣ < 2|E| < 2∣ E ∣ b f s bfs b f s O ( 2 ∣ E ∣ ) O(2|E|) O ( 2∣ E ∣ ) O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
2. BFS增广次数
2.1 增广路长度非递减
即证明算法过程中的 s s s t t t s s s v v v G f G_f G f G f ′ G_{f'} G f ′ v v v s s s v v v 非递减 ,即有 d ′ ( s , v ) ≥ d ( s , v ) d'(s, v) ≥ d(s, v) d ′ ( s , v ) ≥ d ( s , v ) 只能证明非递减而无法证明严格递增 ,即不是 d ′ ( s , v ) > d ( s , v ) d'(s, v) > d(s, v) d ′ ( s , v ) > d ( s , v )
假设某一次 s − t s - t s − t s s s s s s v v v
(1) d ′ ( s , v ) < d ( s , v ) d'(s, v) < d(s, v) d ′ ( s , v ) < d ( s , v )
令 u u u G f ′ G_{f'} G f ′ v v v s s s
(2) d ′ ( s , u ) + 1 = d ′ ( s , v ) d'(s, u) + 1= d'(s, v) d ′ ( s , u ) + 1 = d ′ ( s , v )
如 2.1.1 所述,v v v G f ′ G_{f'} G f ′ G f G_f G f s s s u u u v v v s s s G f ′ G_{f'} G f ′ G f G_f G f s s s
(3) d ( s , u ) ≤ d ′ ( s , u ) d(s, u) ≤ d'(s, u) d ( s , u ) ≤ d ′ ( s , u )
假设 ( u , v ) ∈ E f (u, v) ∈ E_f ( u , v ) ∈ E f s s s v v v d ( s , v ) d(s, v) d ( s , v )
(4) d ( s , u ) + 1 = d ( s , v ) d(s, u) + 1 = d(s, v) d ( s , u ) + 1 = d ( s , v )
结合(1)、(2)、(3)有
d ( s , u ) ≤ d ′ ( s , u ) → d ( s , u ) + 1 ≤ d ′ ( s , u ) + 1 = d ′ ( s , v ) < d ( s , v ) d(s, u) ≤ d'(s, u) → d(s, u) + 1 ≤ d'(s, u)+ 1 = d'(s, v) < d(s, v) d ( s , u ) ≤ d ′ ( s , u ) → d ( s , u ) + 1 ≤ d ′ ( s , u ) + 1 = d ′ ( s , v ) < d ( s , v )
(5) d ( s , u ) + 1 < d ( s , v ) d(s, u) + 1 < d(s, v) d ( s , u ) + 1 < d ( s , v )
(4) 是由 2.1.3 的假设得到的,与由 (1), (2), (3) 得到的 (5) 矛盾,故在 2.1.1 假设成立的前提下,2.1.3 的假设 ( u , v ) ∈ E f (u, v) ∈ E_f ( u , v ) ∈ E f ( u , v ) ∉ E f (u, v) ∉ E_f ( u , v ) ∈ / E f d ′ ( s , v ) > d ( s , v ) d'(s, v) > d(s, v) d ′ ( s , v ) > d ( s , v ) d ′ ( s , v ) ≤ d ( s , v ) d'(s, v) ≤ d(s, v) d ′ ( s , v ) ≤ d ( s , v ) d ( s , u ) + 1 ≤ d ( s , v ) d(s, u) + 1 ≤ d(s, v) d ( s , u ) + 1 ≤ d ( s , v )
由上述知 ( u , v ) ∉ E f (u, v) ∉ E_f ( u , v ) ∈ / E f ( u , v ) ∈ E f ’ (u, v) ∈ E_{f’} ( u , v ) ∈ E f ’ G f G_f G f ( v , u ) (v, u) ( v , u ) G f ′ G_{f'} G f ′ ( u , v ) (u, v) ( u , v ) G f G_f G f
(6) d ( s , u ) = d ( s , v ) + 1 d(s, u) = d(s, v) + 1 d ( s , u ) = d ( s , v ) + 1
(6) 与 (5) 矛盾,于是最初 2.1.1 的假设不成立,即不存在这样的顶点 v v v v v v 非递减 , 故EK算法寻找的增广路长度非递减 。
2.2 增广次数
假设某次 G f G_f G f ( u , v ) (u, v) ( u , v ) ( u , v ) ∉ E f ′ (u, v) ∉ E_{f'} ( u , v ) ∈ / E f ′ ( v , u ) ∈ E f ′ (v, u) ∈ E_{f'} ( v , u ) ∈ E f ′ ( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) G f G_f G f ( u , v ) (u, v) ( u , v )
(7) d ( s , v ) = d ( s , u ) + 1 d(s, v) = d(s, u) + 1 d ( s , v ) = d ( s , u ) + 1
若 ( u , v ) (u, v) ( u , v ) G f ′ G_{f'} G f ′ ( v , u ) (v, u) ( v , u ) G f ′ G_{f'} G f ′
(8) d ′ ( s , u ) = d ′ ( s , v ) + 1 d'(s, u) = d'(s, v) + 1 d ′ ( s , u ) = d ′ ( s , v ) + 1
由 2.1 的结论,s s s d ′ ( s , v ) ≥ d ( s , v ) d'(s, v) ≥ d(s, v) d ′ ( s , v ) ≥ d ( s , v )
d ′ ( s , u ) = d ′ ( s , v ) + 1 ≥ d ( s , v ) + 1 = d ( s , u ) + 2 d'(s, u) = d'(s, v) + 1 ≥ d(s, v) + 1 = d(s, u)+ 2 d ′ ( s , u ) = d ′ ( s , v ) + 1 ≥ d ( s , v ) + 1 = d ( s , u ) + 2
(9) d ′ ( s , u ) ≥ d ( s , u ) + 2 d'(s, u) ≥ d(s, u) + 2 d ′ ( s , u ) ≥ d ( s , u ) + 2
也就是说,( u , v ) (u, v) ( u , v ) s s s u u u s s s ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 ( u , v ) (u, v) ( u , v ) ( ∣ V ∣ − 1 ) / 2 (|V| - 1) / 2 ( ∣ V ∣ − 1 ) /2 < 2 ∣ E ∣ < 2|E| < 2∣ E ∣ 所有边的总的增广次数必小于 2 ∣ E ∣ ∗ ( ∣ V ∣ − 1 ) / 2 2|E|*(|V| - 1)/2 2∣ E ∣ ∗ ( ∣ V ∣ − 1 ) /2 增广次数复杂度为 O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ ) 。
综上,EK 算法复杂度为 O ( ∣ V ∣ ∣ E ∣ 2 ) O(|V||E|^2) O ( ∣ V ∣∣ E ∣ 2 )
证明过程中 BFS增广使得增广路长度非递减 的结论是关键,网上有的文章声称 BFS 寻找增广路的操作使得增广路长度递增,但我们已经在 2.1.3 的叙述中指出这是不对的。根据 2.1 的证明,只能得到 非递减 的结果,但这一结论在 2.2 中足以证明任意边第二次成为饱和边时其最短路径长至少增加2,由此得到BFS次数的上界。
空间复杂度:存图空间为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ )
代码
现给出 EK 算法解决 P3376 【模板】网络最大流 一题的代码(通过)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 package com.yukiyama.demo;import java.util.*;import java.io.*;public class EK { boolean [] visited; int [] ends, heads, nexts, weights, preEdges, pre, saturatedWeights; int edgeNum; public static void main (String[] args) { Scanner cin = new Scanner (System.in); int n = cin.nextInt(), m = cin.nextInt(), s = cin.nextInt() - 1 , t = cin.nextInt() - 1 ; EK demo = new EK (); demo.visited = new boolean [n]; demo.ends = new int [2 * m + 2 ]; demo.nexts = new int [2 * m + 2 ]; demo.weights = new int [2 * m + 2 ]; demo.preEdges = new int [n]; demo.heads = new int [n]; demo.pre = new int [n]; demo.saturatedWeights = new int [n]; demo.edgeNum = 1 ; demo.init(m, cin); cin.close(); System.out.println(demo.ek(s, t)); } public long ek (int s, int t) { long max = 0 ; while (bfs(s, t)) { max += update(s, t); Arrays.fill(visited, false ); } return max; } private void init (int m, Scanner cin) { for (int i = 0 ; i < m; i++) { int u = cin.nextInt() - 1 , v = cin.nextInt() - 1 , weight = cin.nextInt(); ++edgeNum; ends[edgeNum] = v; weights[edgeNum] = weight; nexts[edgeNum] = heads[u]; heads[u] = edgeNum; ++edgeNum; ends[edgeNum] = u; weights[edgeNum] = 0 ; nexts[edgeNum] = heads[v]; heads[v] = edgeNum; } } private boolean bfs (int s, int t) { if (s == t) return false ; Queue<Integer> q = new ArrayDeque <>(); q.add(s); visited[s] = true ; saturatedWeights[s] = Integer.MAX_VALUE; while (!q.isEmpty()) { int u = q.remove(); for (int edgeNo = heads[u]; edgeNo != 0 ; edgeNo = nexts[edgeNo]) { int v = ends[edgeNo], weight = weights[edgeNo]; if (visited[v] || weight == 0 ) continue ; saturatedWeights[v] = Math.min(saturatedWeights[u], weight); q.add(v); visited[v] = true ; preEdges[v] = edgeNo; pre[v] = u; if (v == t) return true ; } } return false ; } private int update (int s, int t) { int cur = t; while (cur != s) { int edge = preEdges[cur]; weights[edge] -= saturatedWeights[t]; weights[edge ^ 1 ] += saturatedWeights[t]; cur = pre[cur]; } return saturatedWeights[t]; } }
Dinic (Dinitz)
算法描述
Dinic算法 (迪尼克算法) :EK 算法以 b f s bfs b f s b f s bfs b f s d f s dfs df s 高度标号 (层次标号) 和 分层图 的概念。以 b f s bfs b f s s s s t t t s s s s s s t t t b f s bfs b f s d f s dfs df s 一个阶段 ,一个阶段的发送流总和为此分层图的 阻塞流 。一个阶段结束后,将此阶段阻塞流累计到最大流中,接着重置高度标号信息,再次执行 b f s bfs b f s d f s dfs df s s s s t t t s s s t t t
高度标号的作用:在以 d f s dfs df s u u u v v v v v v u u u 按步增长到最后一层 的 t t t
算法过程
给定一张图 G ( V , E ) G(V, E) G ( V , E ) s s s t t t G G G s s s t t t f f f
设置一张残留网络 (残留图/残差图/残余图) G f G_f G f G f G_f G f G G G
调用 b f s bfs b f s G f G_f G f t r u e true t r u e f a l s e false f a l se
求增广路发送流。以 d f s dfs df s s s s t t t p p p c c c d f s dfs df s p p p t t t c c c c c c c c c
求阻塞流。反复求上述增广路发送流,并累积到当前分层图阻塞流中。在步骤 3 中,当前分层图完成所有增广由于已无增广路,不会递进到基本情形 (不会遇到 t t t
累计分层图阻塞流,清空所有顶点的高度标号信息 ,再次调用 b f s bfs b f s b f s bfs b f s f a l s e false f a l se s s s t t t s s s t t t
实例分析
以下图为例,增广过程如下:
第一次:s > a > c > t , s>a>c>t, s > a > c > t , r e t u r n return re t u r n r e t u r n return re t u r n r e t u r n return re t u r n t > c > a > s t>c>a>s t > c > a > s s > a > c > t > c > a > s s>a>c>t>c>a>s s > a > c > t > c > a > s
第二次:s > a > c s>a>c s > a > c ( c , t ) (c, t) ( c , t ) a a a d d d d > t d>t d > t r e t u r n return re t u r n t > d > a > s t>d>a>s t > d > a > s s > a > c > d > t > d > a > s s>a>c>d>t>d>a>s s > a > c > d > t > d > a > s
第三次:从 s s s ( s , a ) (s, a) ( s , a ) s s s b b b b > d > t b>d>t b > d > t r e t u r n return re t u r n t > d > b > s t>d>b>s t > d > b > s 2 2 2 s > b > d > t > d > b > s s>b>d>t>d>b>s s > b > d > t > d > b > s
第四次:从 s s s f o r for f or
时空复杂度
以下证明 Dinic 算法时间复杂度为:O ( ∣ V ∣ 2 ∣ E ∣ ) O(|V|^2|E|) O ( ∣ V ∣ 2 ∣ E ∣ )
如下证明参考了COMPSCI 638: Graph Algorithms, Lecture3 。
1. BFS建立分层图
时间复杂度为 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ )
2. 一次DFS增广
在分层图中,由于高度标号加一的判断条件限制, d f s dfs df s s s s t t t d f s dfs df s ∣ V ∣ − 1 |V|-1 ∣ V ∣ − 1 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
3. 一个阶段中DFS增广次数
在分层图中,每次 d f s dfs df s ( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) 增广路只能沿着高度递增的方向 ,而同一阶段内(同一张分层图中)反向边是沿着高度递减方向增加的。( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) 再次强调 ,在 同一阶段内 (同一张分层图中),( v , u ) (v, u) ( v , u ) 高度递减 的,不可能出现在增广路上,因此一条高度递增边 ( u , v ) (u, v) ( u , v ) ∣ E ∣ |E| ∣ E ∣ 一个阶段内 d f s dfs df s ∣ E ∣ |E| ∣ E ∣ O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) 。结合 2 可知,一个阶段的总复杂度为单次 d f s dfs df s d f s dfs df s O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ ) 。
4. 阶段数 (分层图建立次数)
此证明是难点。 如前述,在层高递增条件的限制下,s − t s - t s − t t t t ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 s − t s - t s − t 「严格」递增 ,则立即推出阶段数(分层图建立次数)的上限为 ∣ V ∣ |V| ∣ V ∣ O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
令相邻的两次分层图为 G f G_f G f G f ′ G_{f'} G f ′ d ( u , v ) d(u, v) d ( u , v ) d ′ ( u , v ) d'(u, v) d ′ ( u , v ) G f G_f G f G f ′ G_{f'} G f ′ u u u v v v
由 Edmonds-Karp算法复杂度证明 已知 (这一点很重要),删正向边加反向边的操作,使得源点 s s s u u u 的,即 必有 d ′ ( s , u ) ≥ d ( s , u ) d'(s, u) ≥ d(s, u) d ′ ( s , u ) ≥ d ( s , u ) t t t u u u t t t 必有 d ′ ( u , t ) ≥ d ( u , t ) d'(u, t) ≥ d(u, t) d ′ ( u , t ) ≥ d ( u , t )
(1) d ′ ( s , u ) ≥ d ( s , u ) d'(s, u) ≥ d(s, u) d ′ ( s , u ) ≥ d ( s , u )
(2) d ′ ( u , t ) ≥ d ( u , t ) d'(u, t) ≥ d(u, t) d ′ ( u , t ) ≥ d ( u , t )
对于 s − t s - t s − t d ′ ( s , t ) ≥ d ( s , t ) d'(s, t) ≥ d(s, t) d ′ ( s , t ) ≥ d ( s , t ) 拿掉该不等式中的等号 ,证明 G f ′ G_{f'} G f ′ G f G_f G f d ′ ( s , t ) > d ( s , t ) d'(s, t) > d(s, t) d ′ ( s , t ) > d ( s , t ) 反证法证明不可能取等号 。
假设 d ′ ( s , t ) ≥ d ( s , t ) d'(s, t) ≥ d(s, t) d ′ ( s , t ) ≥ d ( s , t ) 。G f ′ G_{f'} G f ′ s s s t t t f ′ f' f ′ ( x , y ) ∈ E f ′ (x, y) ∈ E_{f'} ( x , y ) ∈ E f ′ G f G_f G f E f ′ E_{f'} E f ′ G f G_f G f d ′ ( s , t ) = d ( s , t ) d'(s, t) = d(s, t) d ′ ( s , t ) = d ( s , t ) f ′ f' f ′ G f G_f G f 一定 已经被找到了。因此在 G f G_f G f ( y , x ) ∈ E f (y, x) ∈ E_f ( y , x ) ∈ E f
(3) d ( s , x ) = d ( s , y ) + 1 d(s, x) = d(s, y) + 1 d ( s , x ) = d ( s , y ) + 1
由 (1) 和 (2) 易知
(4) d ′ ( s , x ) ≥ d ( s , x ) d'(s, x) ≥ d(s, x) d ′ ( s , x ) ≥ d ( s , x )
(5) d ′ ( y , t ) ≥ d ( y , t ) d'(y, t) ≥ d(y, t) d ′ ( y , t ) ≥ d ( y , t )
f ′ f' f ′ d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t ) d'(s, t) = d'(s, x) + 1 + d'(y, t) d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t )
d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t ) ≥ d ( s , x ) + 1 + d ( y , t ) d'(s, t) = d'(s, x) + 1 + d'(y, t) ≥ d(s, x) + 1 + d(y, t) d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t ) ≥ d ( s , x ) + 1 + d ( y , t )
又由 (3) 得到
d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t ) ≥ d ( s , x ) + 1 + d ( y , t ) = d ( s , y ) + d ( y , t ) + 2 d'(s, t) = d'(s, x) + 1 + d'(y, t) ≥ d(s, x) + 1 + d(y, t) = d(s, y) + d(y, t) + 2 d ′ ( s , t ) = d ′ ( s , x ) + 1 + d ′ ( y , t ) ≥ d ( s , x ) + 1 + d ( y , t ) = d ( s , y ) + d ( y , t ) + 2
即
(6) d ′ ( s , t ) ≥ d ( s , t ) + 2 d'(s, t) ≥ d(s, t) + 2 d ′ ( s , t ) ≥ d ( s , t ) + 2
由此,d ′ ( s , t ) = d ( s , t ) d'(s, t) = d(s, t) d ′ ( s , t ) = d ( s , t ) d ′ ( s , t ) ≥ d ( s , t ) d'(s, t) ≥ d(s, t) d ′ ( s , t ) ≥ d ( s , t ) d ′ ( s , t ) > d ( s , t ) d'(s, t) > d(s, t) d ′ ( s , t ) > d ( s , t ) Dinic 算法中下一分层图的最短路径长度与前一分层图相比严格递增 。
综上,总时间复杂度为每个阶段建立分层图的复杂度 O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) d f s dfs df s O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ( ∣ E ∣ + ∣ V ∣ ∣ E ∣ ) ∗ ∣ V ∣ ) O((|E|+|V||E|)*|V|) O (( ∣ E ∣ + ∣ V ∣∣ E ∣ ) ∗ ∣ V ∣ ) O ( ∣ V ∣ 2 ∣ E ∣ ) O(|V|^2|E|) O ( ∣ V ∣ 2 ∣ E ∣ )
空间复杂度:采用邻接表存图,则存图空间为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V|+|E|) O ( ∣ V ∣ + ∣ E ∣ ) O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) b f s bfs b f s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) d f s dfs df s O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
代码
实战应用
给出以下图论相关题目及作者写的题解,供读者在阅读本文后自练自查。
※ 不断更新中。
1 2 3 4 5 6 7 8 UF: Union-Find 并查集 FS: DFS & BFS 深搜和广搜 Topo: Topological Sort 拓扑排序 SP: Shortest Path 最短路 MST: Minimum Spanning Tree 最小生成树 MF: Maximum Flow 最大流 标记 〇 表示该题与该算法相关。
【更新日志】
[2022-09-20]
修改了 Bellman-Ford 方法求解 743. 网络延迟时间 的代码中的一处 bug 。即若本次全量松弛执行了松弛操作,则 finished = false ,随后在开始下一次全量松弛前应将 finished 置回 true。感谢 @nTouKxAnj3 (@河) 、 @rain-roc (@RainRoc) 指出。
[2022-09-08]
新增了 Prim 算法正确性证明小节。(小节路径: 最小生成树 > Prim > 朴素版 > 正确性证明)
[2022-07-17]
大幅修改了「最大流最小割定理」中的「证明 k = m k=m k = m
[2022-07-16]
在「最大流最小割定理」一节的「最小割的大小」小节中,原文称「现在我们来指出一个 l = 4 l = 4 l = 4 s − t s-t s − t
在「Edmonds-Karp」-「时间复杂度」-「2.2 增广次数」中,原文称「…之后 ( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) ( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) 增广路上的边 …」,后续论证仍然成立。
上述两点均由 @migeater 指出,非常感谢!🙏
[2022-07-01]
[2022-06-20]
[2022-06-19]
在「图的表示」一节中新增「链式向前星」小节,并在后续代码中给出此存图方式的代码实例。