Bellman-Ford

算法描述

Bellman-Ford Algorithm(贝尔曼-福特算法): 与 Dijkstra 算法的相同点是对边 (或者说对顶点) 不断执行松弛操作 ，以逐渐得到所有顶点到源点的最短距离。Dijkstra每次循环完成 一个 顶点最短路径的确定，而 BF 算法则对图的 所有边 (∣E∣|E| 条边) ，简单地进行 ∣V∣−1|V|-1 次 全量松弛操作 ，第 ii 次「全量松弛」使得位于第 i+1i+1 层的顶点的距离被确定 (详见后文)，因而 BF 算法也是「贪心」思想的应用。又因为任意顶点最多居于第 ∣V∣|V| 层 (以源点 ss 为第 1 层)，因此算法结束时，保证 (无负圈图) 所有顶点距离最短。


算法过程

  1. 置源点 ss 的距离为 0。

  2. 外层循环执行 ∣V∣−1|V|-1 次，每一次都「松弛所有边」。

  3. 进入外层循环后按顶点顺序依次对所有顶点 vv 考察其所有邻接顶点 ww 是否有 dv+∣(v,w)∣<dwdv + |(v, w)| < dw，若有，松弛之，即令 dw=dv+∣(v,w)∣dw = dv + |(v, w)|。

  4. 在一次「松弛所有边」的操作中，若没有任何边被松弛，则退出最外层循环，表明所有可能的松弛已完成 (负圈图除外)。

  5. 检查图是否有负圈。做法是再对所有边执行松弛操作，若有边可被松弛，则有负圈，结束程序，否则正常结束，所有顶点最短路径被求出。


正确性证明(说明)

  1. 已知若一个顶点 vv 的所有入边若完成了所有可能的松弛 (一条入边可被多次松弛)，则在 最后一次松弛 后，必有 dv=δvdv=δv 。 (dvdv 表示由算法得到的 vv 的距离， δvδv 表示实际的 vv 的最短距离)。

  2. 易知，第 ii 次全量松弛，第 ii 层顶点的出边 必被松弛 。例如第 1 次全量松弛，ss (第 1 层顶点) 的出边必被松弛。第 2 次全量松弛，由于有了第 1 次全量松弛的结果，ss 的邻接顶点 (第 2 层顶点) 的出边必被松弛。

  3. p(s,v)p(s, v) 路径长 (边数) 最长不会超过 ∣V∣−1|V|-1 ，当 ss 到 vv 为链状时最长 ∣V∣−1|V|-1 。当 vv 的入边是第 1 层入边时，将在第 1 次全量松弛时被松弛，若是第 2 层入边，则会在第 2 次全量松弛时被松弛 (这条入边的发出顶点在第 1 次全量松弛时已被松弛)，以此类推，第 ii 层入边会在第 ii 次全量松弛时被松弛。所有顶点的入边组成了该图的所有边，任意一边一定是某一层次的入边 (可以同时属于多个层次) 。某一层顶点距离的更新，一定来自其入边的松弛。

  4. 由此，vv 的入边能否被全部松弛只取决于最深的入边能否被松弛 (当一条入边属于多个层次时，取其最深层次)，也即取决于 ss 到 vv 的最长路径 max⁡{∣p(s,v)∣,v∈V}\max\{|p(s, v)|, v ∈ V\}的长度。如前述， max⁡{∣p(s,v)∣,v∈V}≤∣V∣−1\max\{|p(s, v)|, v ∈ V\} ≤ |V|-1 ，故至多经过 ∣V∣−1|V| - 1 次全量松弛，图的所有入边必定都松弛过且完成了所有可能的松弛 (某条入边属于多个层次时，可能经过多次松弛) 。如果把图看成以 ss 为根的树，也可以说为了求得所有顶点的最短路径，所需的全量松弛的次数取决于 树的高度 。对某一顶点，可以说该顶点至多经过其最大深度减 1 次全量松弛后取得最短路径。

  5. 上述过程对任意顶点均成立，故 BF 算法正确性得证。

此证明也可以看作如下「动态规划」过程。且为较简单的单串单依赖动态规划 (单依赖指当前元素的更新只依赖前一元素)。

  1. 定义: dp[j]dp[j] 表示源点 ss 到顶点 jj 的最短路径长度。

  2. 边界: dp[s]=0dp[s] = 0 。

  3. 递推: dp[j]=dp[j−1]+∣(j−1,j)∣dp[j] = dp[j - 1] + |(j - 1, j)| 。j−1j - 1 表示 s−js-j 最短路径上的前一个顶点。

根据前述，j−1j - 1 顶点最大层深必比 jj 小 1，故 dp[j−1]dp[j - 1] 一定在求 dp[j]dp[j] 之前就已求出，递推式成立。


实例说明

以下实际考察 BF 算法对下图的求解过程，重点关注顶点 vv 。 (图裂了的话可以看这里)

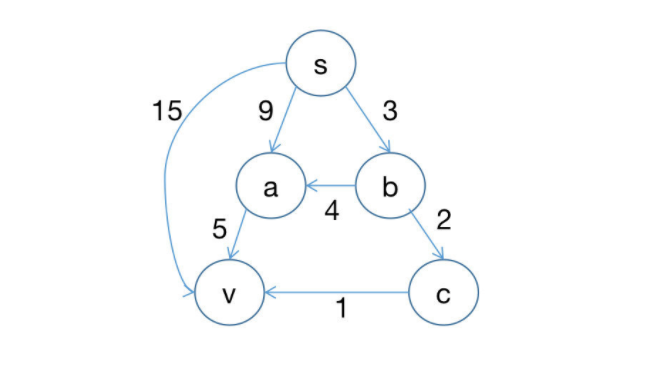
image.png

p(s,v)p(s, v) 有如下四种可能：

p1:s>v，∣p1∣=15p1: s > v ，|p1| = 15 ，(s,v)(s, v) 是 vv 的第 1 层入边

p2:s>a>v，∣p2∣=14p2: s > a > v，|p2| = 14 ，(a,v)(a, v) 是 vv 的第 2 层入边

p3:s>b>a>v，∣p3∣=12p3: s > b > a > v ，|p3| = 12 ，(a, v) 是 vv 的第 3 层入边

p4:s>b>c>v，∣p4∣=6p4: s > b > c > v ，|p4| = 6 ，(c,v)(c, v) 是 vv 的第 3 层入边

可以看到 (a,v)(a, v) 边同时属于 vv 的第 2 和第 3 层入边。这四条路径最长者长 3 (指边数，p3p3 和 p4p4 )，根据上述分析，只需要执行 3 次全量松弛即可完成对 vv 最短路径的确定。又因为源点到所有顶点的所有路径中最长的长度也是 3，所以执行 3 次全量松弛可以确定所有顶点的最短路径。假设全量松弛时顶点的处理顺序为 s,a,c,b,vs, a, c, b, v ，下表展示算法对该图的运行过程 (第 3 次之后的全量松弛不会再松弛任何边，省略)。

松弛过程 dsds dada dcdc dbdb dvdv
初始 0 (*) ∞ ∞ ∞ ∞
第1次全量松弛 0 ∞ > 9 ∞ ∞ > 3 (*) ∞ > 15
第2次全量松弛 0 9 > 7 (*) ∞ > 5 (*) 3 15 > 14
第3次全量松弛 0 7 5 3 14 > 12 > 6 (*) 
1
2
3
4
5
6
7
8
备注：
1. 初始时令 ds 为0，(*)表示已取得该顶点最短路径。
2. 第1次。(s, a), (s,b), (s, v)属于第1层入边，被松弛。
   且b只有一条入边，即经过这趟松弛操作，使得 db = δb。
3. 第2次。第1层入边不会再被松弛。第2层入边(a, v), (b, a), (b, c)被松弛。
   经过这趟松弛操作，a, c的全部入边松弛完毕，使得 da = δa，dc = δc。
4. 第3次。第1，2层入边不会再被松弛，第3层入边(a, v), (c, v)被松弛。
   v 的全部入边松弛完毕，使得 dv = δv。

负边图 & 负圈图

  • 负边图。由于该算法在 ∣V∣−1|V|-1 次对所有边的松弛操作中会穷尽所有边被松弛的可能，类似以拓扑排序方式针对 DAG 图的 Dijkstra 算法 (通过入度为 0 保证穷尽所有松弛的可能)，所以也适用于有负边的图。

  • 负圈图。当图存在负圈时，ss 到圈上任意顶点的距离都可以通过不断绕圈趋于无限小。因此若不能保证输入的图无负圈，可以在 ∣V∣−1|V| - 1 次全量松弛后再执行一次全量松弛，若仍有边可被松弛，说明存在负圈。


提前结束优化

当某一次全量松弛过程中没有边被松弛，说明所有可能的松弛已被穷尽，可提前结束程序。


最坏情形

当图中存在两点间路径长度为 ∣V∣−1|V|-1 ，且在最后一次「全量松弛」时仍有边被松弛时间达到最坏情形。此情况下，需要对所有边执行 ∣V∣−1|V|-1 次松弛后才能求得所有顶点的最短路径。对于一链状图 s>a>b>c>vs > a > b > c > v ，其中 ∣(s,a)∣=1|(s, a)| = 1，∣(a,b)∣=2|(a, b)| = 2，∣(b,c)∣=3|(b, c)| = 3，∣(c,v)∣=4|(c, v)| = 4。 (图裂了的话可以看这里)

image.png

假定每次「全量松弛」均以 v,c,b,a,sv, c, b, a, s 的顺序松弛，程序开始时置源点 ss 的距离为 0。

  1. 第 1 次循环只有 aa 的距离被松弛为 1。

  2. 第 2 次循环 bb 的距离被松弛为 3。

  3. 第 3 次循环 cc 的距离被松弛为 6。

  4. 第 4 次循环 vv 的距离被松弛为 10。

每次全量松弛都对所有边尝试松弛，但只有一个顶点的距离会被更新，经过 ∣V∣−1|V|-1 次即 4 次「全量松弛」后才完成。


时空复杂度

时间复杂度：每次全量松弛要操作 ∣E∣|E| 条边，共 ∣V∣−1|V|-1 次，复杂度为 O((∣V∣−1)∣E∣)O((|V|-1)|E|) ，即 O(∣V∣∣E∣)O(|V||E|) 。

空间复杂度：不考虑图的存储空间，为 O(1)O(1) 。


SPFA

算法描述

SPFA算法(最短路径快速算法)：SPFA 算法是对 BF 算法的一种改进。在BF 算法的说明中我们指出，第 ii 次「全量松弛」操作，只有第 i+1i+1 层的顶点距离会被更新至最短，这明显具有 BFS 特点，因此可以考虑不通过「全量松弛」来松弛第 i+1i+1 层顶点，而是以 BFS 的方式，借助队列 qq ，每松弛一层顶点，将它们入队，出队时，尝试松弛到其所有邻接顶点的距离，即可在第 ii 层顶点出队时松弛第 i+1i+1 顶点并使这些第 i+1i+1 顶点距离取得最小。因为顶点「按层」入队出队，层深最大为 ∣V∣|V| (无负圈图)，因此算法可以结束。

我们还可以这样看，一个顶点 ww 的距离能够被更新，隐含着这样一个 前提 ：ww 的前驱 vv 的距离被更新过 。因为 dv+∣(v,w)∣<dwdv + |(v, w)| < dw 时才会更新 dwdw，而 ∣(v,w)∣|(v, w)| 是不变的，初始时 dvdv 和 dwdw 都是无穷大，所以只有 dvdv 更新 (变小)，dwdw 才会更新 (变小)。从源点出发指向其邻接顶点，对一个连通的有向图，总能遍历所有顶点，每次考察已松弛的顶点 vv 是否能松弛其邻接顶点 ww ，ww 成为已松弛的顶点后再考察是否能松弛 ww 的邻接顶点，重复此操作直到「当前已松弛顶点均无法再松弛任何顶点」为止。设置一个队列 qq，程序开始时置源点s的距离为 0，ss 入队。while 对 qq 判空，不空时队首顶点 vv 出队，松弛其边 (即更新 vv 的邻接顶点 ww 的距离)，根据上述分析，如果 dwdw 被更新，那它的邻接顶点将 有机会被更新 ，所以将 ww 入队，等待出队时尝试松弛 ww 的边。需要注意的是，ww 入队前需要检查当前队列中是否已有 ww ，若有则无需入队。该检查使得时间复杂度为 O(∣V∣∣E∣)O(|V||E|) ，否则这一复杂度将无法得到保证。重复上述过程，当 qq 为空时 (无负圈图) 代表所有被更新过距离的顶点，都 无法再触发其邻接顶点距离的更新 。也可以说对任意一个顶点 vv 来说，ss 到 vv 的所有路径带来的所有可能的对 dvdv 的更新已被穷尽。程序结束时得到所有顶点到源点的最短路径。


算法过程

  1. 初始时所有顶点距离为 InfinityInfinity。设置一个队列 qq，置源点 ss 的距离为 0，ss 入队。

  2. 设置一个用于支持负圈检测的记录所有顶点入队次数的哈希表。

  3. 以 while 循环对 qq 判空，若 qq 不空，队首顶点 vv 出队。

  4. 遍历 vv 的邻接顶点 ww ，若满足松弛条件，则更新 ww 的距离，置 ww 的前驱为 vv ，若当前队列无 ww 则将 ww 入队。然后检查 ww 的入队次数是否大于 ∣V∣−1|V| - 1，若大于则表示存在负圈，结束程序，否则将 ww 入队次数加 1。


正确性证明(说明)

SPFA 算法与 BF 算法的核心内容都在于 穷尽所有路径带来的所有可能的松弛 。BF 算法通过 ∣V∣−1|V|-1 次全量松弛达到 (详见BF算法正确性证明)，第 ii 次全量松弛中，有效松弛仅作用于第 i+1i+1 层顶点，其他层深顶点已不能够被松弛却还是会被尝试，这就产生了冗余操作。SPFA 算法利用顶点的距离能够被松弛的隐含前提，通过队列来减少松弛顶点距离的次数。第 ii 层顶点出队时发生的松弛，效果上相当于 BF 算法外层循环第 ii 次对所有边的全量松弛。在连通且无负圈的情况下，按层推进一定能够执行最大层深第 ∣V∣|V| 层，因此该算法是正确的。


实例说明

仍以前一张网络图为例考察 SPFA 算法的求解过程，进一步看清其正确性及 SPFA 与 BF 的关系。

第 1 层顶点只有 ss ，所以第 2 步 ss 出队相当于 BF 算法中第 1 次全量松弛。a,b,va,b,v 是第 2 层顶点，所以第 3，4，5 步相当于 BF 算法中第 2 次全量松弛。此时 v,a,cv,a,c 是第 3 层顶点 (根据所在路径层深的不同，一个顶点可以属于不同层) ，所以接下来的第 6，7 相当于 BF 算法中的第 3 次全量松弛。最后一步使得队列为空，结束。

松弛过程 dsds dada dcdc dbdb dvdv 队列 qq
1. 初始 0 (*) ∞ ∞ ∞ ∞ s;
2. s出 0 ∞ > 9 ∞ ∞ > 3 (*) ∞ > 15 a, b, v;
3. a出 0 9 ∞ 3 15 > 14 b, v;
4. b出 0 9 > 7 (*) ∞ > 5 (*) 3 14 v; a, c
5. v出 0 7 5 3 14 a, c;
6. a出 0 7 5 3 14 > 12 c; v
7. c出 0 7 5 3 12 > 6 (*) v;
8. v出 0 7 5 3 14 空 
1
2
3
4
5
6
7
8
9
10
11
1. 初始时令 ds 为0，(*)表示已取得该顶点最短路径。「;」是层的分隔符。
2. s 出队时松弛 (s, a), (s,b), (s, v)。
   且 b 只有一条路径，即经过这趟松弛操作，使得 db = δb。
3. a 出队时松弛 (a, v)，这是 v 的距离第 2 次被松弛。
4. b 出队时松弛 (b, a), (b, c)，a 有两条路径，c 只有一条，
   于是 da = δa，dc = δc。
5. 无可松弛边。
6. a 出队时松弛 (a, v)，这是 v 的距离第 3 次被松弛。
7. c 出队时松弛 (c, v)，这是 v 的距离第 4 次被松弛。
   此时 p(s, v) 所有可能的路径带来的 v 的入边的松弛均已完成，于是 dv = δv 。
8. 无可松弛边，队列空，程序结束。

负边图 & 负圈图

  • 负边图。SPFA 能够处理有负权的非负圈图，原因与 BF 算法一样，因为算法会处理所有顶点的 所有可能的距离更新 。

  • 负圈图。若图存在负圈，负圈上的顶点将无限循环入队，算法无法结束。可以记录顶点入队的次数， 一个顶点入队次数大于 ∣V∣−1|V|-1 时，该图存在负圈，此时即可结束程序。

负圈判定： 记录保存每个顶点入队的次数(例如用哈希表记录)，顶点 vv 的距离更新后判断当前更新次数是否超过了 ∣V∣−1|V|-1 次，若超过则说明存在负圈，若不超过则将更新次数加 1。以层为单位追踪顶点入队出队的过程，不难理解无负圈情况下，一个顶点的距离至多被松弛 (顶点入队) ∣V∣−1|V|-1 次，若超过则说明存在经过该顶点的负圈。

当图只有一个节点时，要小心处理负圈检测。如下伪代码，次数检测写在次数加一之前可以避免单节点图被误判为负圈。

1
2
3
4
5
6
7
if(!q.contains(w)) { // 检查w是否已经在q中
    q.add(w) // 将w加入队列  
    if(w.inCount > |V| - 1) { // 若大于|V|-1则检出负圈
        System.err.println("存在负圈！")
    }
    w.inCount++ // 记录入队次数
}

当然也可以调换次数检测和加一的顺序，并把 >∣V∣−1> |V| - 1 改成 >∣V∣> |V| ，如下，效果相同。

1
2
3
4
5
6
7
if(!q.contains(w)) { // 检查w是否已经在q中
    q.add(w) // 将w加入队列  
    w.inCount++ // 记录入队次数
    if(w.inCount > |V|) { // 若大于|V|则检出负圈
        System.err.println("存在负圈！")
    }
}

时空复杂度

时间复杂度：O(∣V∣∣E∣)O(|V||E|) 。为方便说明，列出 SPFA 伪代码如下。

1
2
3
4
5
6
7
8
9
10
11
SPFA (Bellman-Ford-Moore) 算法伪代码:
1    Queue q
2    q.add(s) // s的距离初始为0, 其他顶点的距离初始为Infinity

3    while(!q.isEmpty())
4        v = q.remove()
5        for (w : v.adjs)  // w是v的邻接顶点
6            if(dv + d(v, w) < dw)
7                dw = dv + d(v, w)
8                if(!q.contains(w)) //检查w是否在当前队列中，不在则入队
9                    q.add(w)

按层分析很容易得到 SPFA 的复杂度。顶点一层一层地入队出队，一张图最多有 ∣V∣|V| 层 (以 ss 为第 1 层)，所以 按层计 ，任何顶点最多只能入队 ∣V∣−1|V| - 1 次。第 1 层顶点个数为 1，其余每层顶点数不会超过 ∣V∣−1|V| - 1 （第8行所保证）。再次强调，虽然一个顶点可能会通过不同的路径重复属于某一层，例如 s>a>c，s>b>cs > a > c，s > b > c ，但有了第 8 行的检查，使得一个顶点最多只能在一层顶点里出现一次。考虑每层顶点个数小于 ∣V∣|V| ，每层顶点的松弛次数少于 ∣E∣|E| 次，因此复杂度为 O(∣V∣∣E∣)O(|V||E|) 。

第 8 行 if(!q.contains(w)) 是SPFA 作为改进 BF 的关键，有必要继续进一步说明为何加了这个检查优化不影响结果的正确性。假设从 ss 经过长度相同的不同路径到达若干个不同顶点，这些顶点都指向 vv ，每条路径带来的松弛都能执行到 (BFS 所保证)，只是除了第一次之外不把 vv 放入队列。将 vv 放入队列的目的是在之后使其邻接顶点 ww 有被松弛的机会。对于 ww ，来自 vv 的松弛机会只需一次即可，所以不每次都将 vv 放入队列中。

SPFA 每出队第 ii 层顶点，使得在最短路径上第 i+1i+1 层的顶点得到松弛。不厌其烦地，SPFA第 ii 层顶点出队的效果等同于 BF 第 ii 轮对边的全量松弛的效果，比 BF 的操作更有效率的地方在于，SPFA 仅仅松弛它够得着得邻边。BF 暴力地松弛所有边，但有效的只有第 i+1i+1 层，其他更深或更浅的顶点无法松弛，但一律以 if(dv + |(v, w)| < dw) 询问了一次。所以说 SPFA 是 BF 的一种改进。

空间复杂度：用于支持负圈检测的哈希表的空间，O(∣V∣)O(|V|) 。

对时间复杂度的分析可以看出，稀疏图中顶点的 p(s,v)p(s, v) 路径平均条数很少，SPFA 实际运行速度会很快。但在稠密图下会达到 O(∣V∣∣E∣)O(|V||E|) 。


Bellman-Ford-Moore 和 SPFA

SPFA 实际上应当称作 Bellman-Ford-Moore 算法。根据Wiki词条 Bellman-Ford algorithm 的介绍，「对所有的边，简单地松弛 ∣V∣−1|V| - 1 轮」的朴素 BF 算法在相近的几年里被三个人分别独立发明。只是不知道什么原因算法名称后来定型成了 Bellman-Ford。

1
2
3
1955年 Alfonso Shimbel
1956年 Lester Ford Jr.
1958年 Richard Bellman

又过了一年，1959年的时候Edward F. Moore提出了BF算法的一个改进，即前文的伪代码 (SPFA / Bellman-Ford-Moore) 。

A variation of the Bellman-Ford algorithm known as Shortest Path Faster Algorithm, first described by Moore (1959), reduces the number of relaxation steps that need to be performed within each iteration of the algorithm.

1994年，西南交通大学的段凡丁在该年4月的《西南交通大学学报》里发表了题为《关于最短路径的SPFA快速算法》的论文，重新提出了Moore的改进 ，并且给了个比较通俗的名字 Shortest Path Fast Algorithm。段老师显然没看过 Moore 当初的论文，否则不会给出一个错误的复杂度估计（给出的复杂度是 O(k∣E∣)O(k|E|) ）。有意思的是，现在用 Google 搜 SPFA，即便在英文论坛，许多人对这个改进也称之为 SPFA，而非 BFM，真可谓是「喧宾夺主」了。