树状数组从入门到下车
感谢官方推荐 🎉😄。
可在作者的 github仓库 中获取本文和其他文章的 markdown 源文件及相关代码。
欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题,我将长期维护所有文章。
所有文章均用 Typora 完成写作,可使用 Typora 打开文章 md 文件,以获得最佳阅读体验。
⚠️⚠️⚠️ 全文一万四千字,外科手术式讲解三种树状数组。抽象的,我们让它具体,难解的,我们条分缕析。
❗️ 【NEW】 ❗️
这是小白 yuki 推出的「树ADT」系列文章的第 10 篇 (10/13) 。
k e y w o r d s keywords k ey w or d s
树状数组 (BIT) / 区间划分 / 前缀和 / l o w b i t lowbit l o w bi t
树状数组 是一种能够高效求解「区间问题」的数据结构。「区间问题」指的是对于大小为 n n n n u m s nums n u m s n u m s nums n u m s O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n )
本文将介绍的树状数组,利用 n u m s nums n u m s 下标二进制表示及其位运算 ,十分巧妙地将输入区间划分为 n n n 同时实现 O ( l o g n ) O(logn) O ( l o g n ) 。
上述文字是对树状数组的高度概括,初学时必然难解其意,但只要读者学完本文,一定会对上述描述有深刻的理解。本文主要内容及编排顺序如下。
基本树状数组 (单点修改区间查询树状数组) : 以 O ( l o g n ) O(logn) O ( l o g n ) n n n 单点修改 及 区间查询 问题。区间划分: 从区间查询问题出发,思考如何利用类似倍增思想的做法来划分子区间,从而提高区间查询的效率。lowbit: 由「划分连续子区间」的需求出发,尝试从元素下标二进制表示入手,找到通过 l o w b i t lowbit l o w bi t 「二元索引树」 。时间复杂度分析: 单点修改及区间查询的时间复杂度都与 ( n ) 2 (n)_2 ( n ) 2 O ( l o g n ) O(logn) O ( l o g n ) 区间修改单点查询树状数组: 在「单点修改区间查询树状数组」的基础上,引入 差分数组 实现区间修改单点查询树状数组。区间修改区间查询树状数组: 在「区间修改单点查询树状数组」的基础上,根据 算式推导 ,引入 辅助树状数组 实现区间修改区间查询树状数组。离散化 : 当区间问题只关心元素之间的大小关系而不关心元素值时,将输入序列离散化,能够提高求解效率或帮助解决一些特定问题。离散化实现包括 松离散 和 紧离散 。指定区间内指定取值范围的元素数 :「求指定区间 [ l , r ] [l,r] [ l , r ] [ l o w e r , u p p e r ] [lower, upper] [ l o w er , u pp er ]
本文原题 「树状数组 (树ADT连载 10/13)」,十分干瘪,不太符合作者的气质,遂改为现标题。「下车」表示作者的一种希望 ,此刻我们开始发车学习树状数组,看完本文,希望读者朋友们能轻松掌握,安全下车。
yuki的其他文章如下,欢迎阅读指正!
如下所有文章同时也在我的 github 仓库 中维护。
[2022-10-16]
再次重写「指定区间内指定取值范围的元素数」一节 (重写三回了。。。😅)。
[2022-10-15]
将原先 t r e e tree t ree [ 1 , n ] [1,n] [ 1 , n ] [ 0 , n − 1 ] [0,n-1] [ 0 , n − 1 ]
几乎重写了「指定区间内指定取值范围的元素数」一节。
[2022-10-14]
[TOC]
树状数组
树状数组 (二元索引树 / 二元下标树 / Binary Indexed Tree, BIT / Fenwick Tree): 树状数组虽名为数组,但从其英文名 (Binary Indexed Tree) 可看出它本质上是一种被表达为树的数据结构。对于大小为 n n n n u m s nums n u m s O ( l o g n ) O(logn) O ( l o g n )
更新 n u m s nums n u m s 单点修改 。
求 n u m s nums n u m s 区间查询 。
对于这两种操作,最简单的做法是直接根据下标操作 n u m s nums n u m s O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) n u m s nums n u m s p r e S u m preSum p re S u m [ l , r ] [l , r] [ l , r ] p r e S u m [ r ] − p r e S u m [ l − 1 ] preSum[r] - preSum[l-1] p re S u m [ r ] − p re S u m [ l − 1 ] O ( 1 ) O(1) O ( 1 ) n u m s [ i ] nums[i] n u m s [ i ] p r e S u m [ i ] preSum[i] p re S u m [ i ] O ( n ) O(n) O ( n )
无论是使用普通数组还是利用前缀和数组,对于上述两种操作,均有一种的时间复杂度为 O ( n ) O(n) O ( n ) n u m s nums n u m s t r e e [ ] tree[] t ree [ ] O ( l o g n ) O(logn) O ( l o g n )
序列操作
数组
前缀和
树状数组
单点修改
O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( l o g n ) O(logn) O ( l o g n )
区间查询
O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( l o g n ) O(logn) O ( l o g n )
树状数组是一种极具巧思,代码实现极轻巧却不失高效的数据结构 。我们马上会看到树状数组如何借助 二进制形式的 n u m s nums n u m s ,将 n u m s nums n u m s O ( l o g n ) O(logn) O ( l o g n )
为方便后续行文,我们提前介绍如下操作,并约定称呼及简称。
操作
定义
单点修改 (Point Update, PU)
修改 n u m s nums n u m s
单点查询 (Point Query, PQ)
查询 n u m s nums n u m s
区间修改 (Range Update, RU)
修改 n u m s nums n u m s
区间查询 (Range Query, RQ)
求 n u m s nums n u m s
根据 wiki,树状数组最早由 Boris Ryabko (前苏联) 于1989年 提出 ,并在1992 年发表了一个 改进版本 。 Peter Fenwick 在其1994年的 文章 中描述了该数据结构,随后此数据结构便以 Fenwick tree 之名广为人知。
This structure was proposed by Boris Ryabko in 1989[1] with a further modification published in 1992.[2] It has subsequently become known under the name Fenwick tree after Peter Fenwick , who described this structure in his 1994 article.[3]
作者的「树状数组」知识,最初学自 OI wiki 树状数组 。
PURQ BIT (单改区查)
最基本的树状数组支持「单点修改 (PU)」和「区间查询 (RQ)」,即 PURQ BIT。
区间划分
我们已经知道,使用普通数组或利用前缀和数组实现 PU / RQ 操作时,各自均有一种操作需要遍历 一段连续的区间 。在 n u m s nums n u m s O ( n ) O(n) O ( n ) 减少操作的次数 。首先考虑求长度为 k k k k k k k k k 划分为多个子区间 ,子区间个数显著地少于 k k k k k k
例如下图,当我们求 n u m s nums n u m s [ 3 , 8 ] [3, 8] [ 3 , 8 ] [ 3 , 4 ] [3,4] [ 3 , 4 ] [ 5 , 7 ] [5,7] [ 5 , 7 ] [ 8 , 8 ] [8,8] [ 8 , 8 ]
那么树状数组是这一想法的实现吗?答案是:不完全是。 树状数组确实将 n u m s nums n u m s [ l , r ] [l,r] [ l , r ] 「前缀区间和」作差 的方式来得到指定区间的「区间和」,前缀区间才是通过若干个连续子区间组成的。
我们提前指出,树状数组这一数据结构,对输入数组 n u m s nums n u m s [ 0 , k ] [0,k] [ 0 , k ] 由划分结果中的若干个连续的子区间构成 ,这些子区间的区间和相加即可得到「前缀区间和」。对于任意区间 [ l , r ] [l,r] [ l , r ] [ 0 , r ] [0, r] [ 0 , r ] [ 0 , l − 1 ] [0,l-1] [ 0 , l − 1 ] [ l , r ] [l,r] [ l , r ]
区间划分的思考也许会让你想到利用「倍增思想」的快速幂算法 leetcode #50-pow(x, n) ,该算法不是通过「连续」地将 x x x n n n 「利用已求出的结果完成下一步计算」 的思想。总之我们需要一种类似倍增方法的能够跳跃式划分区间 (下标) 的方法。
现在,我们重新将 树状数组解决区间和问题 的 灵感来源 描述如下:
n u m s nums n u m s [ l , r ] [l, r] [ l , r ] [ 0 , r ] [0,r] [ 0 , r ] [ 0 , l − 1 ] [0, l-1] [ 0 , l − 1 ] 前缀区间由若干个相邻的子区间构成,这些子区间的区间和相加得到前缀区间的区间和。
也许能够通过某种类似倍增方式划分 n u m s nums n u m s
很抽象,尤其是最后一句,现在无法得知如何处理下标来划分输入区间,不过没关系,我们马上对大小为 8 (下标范围为 [ 0 , 7 ] [0,7] [ 0 , 7 ] n u m s nums n u m s
将指定长度的 n u m s nums n u m s n u m s nums n u m s 可循环的操作 。
n u m s nums n u m s [ l , r ] [l, r] [ l , r ] [ 0 , r ] [0,r] [ 0 , r ] [ 0 , l − 1 ] [0,l-1] [ 0 , l − 1 ] [ 0 , l − 1 ] , [ 0 , r ] [0, l-1], [0,r] [ 0 , l − 1 ] , [ 0 , r ] n u m s nums n u m s 若干相邻区间 所构成。从这里可以看出, 对 n u m s nums n u m s [ 0 , n − 1 ] [0,n-1] [ 0 , n − 1 ] [ 0 , k ] ( k ∈ [ 0 , n − 1 ] ) [0,k](k∈[0,n-1]) [ 0 , k ] ( k ∈ [ 0 , n − 1 ]) [ 0 , k ] ( k ∈ [ 0 , n − 1 ] ) [0,k](k∈[0,n-1]) [ 0 , k ] ( k ∈ [ 0 , n − 1 ]) 子区间的区间和被 实时维护 。需要用一个 t r e e [ ] tree[] t ree [ ] t r e e tree t ree
求给定区间的区间和,即求两次前缀区间和再作差。求前缀区间和需要通过 某种规则 一边寻找其子区间 i i i t r e e [ i ] tree[i] t ree [ i ] i i i
更新 n u m s [ i ] nums[i] n u m s [ i ] 某种规则 更新包含该值的所有子区间的区间和。
「灵感来源」描述中提到了「类似倍增方式」,我们不难想到可以从下标的二进制表示着手。以划分区间 [ 0 , 14 ] [0,14] [ 0 , 14 ] 14 = ( 1110 ) 2 14=(1110)_2 14 = ( 1110 ) 2 n u m s nums n u m s [ 0 , 14 ] [0,14] [ 0 , 14 ] 最右子区间的右界 为 14 , 最左子区间的左界 是 0 。我们将最右子区间作为当前区间,从当前子区间右界下标 14 开始考虑。
一个容易想到的方法如下:
【区间划分方法】:从最右子区间右界 k k k k k k k k k 左邻子区间的右界下标 。重复该操作直到当前区间右界下标为 0 (二进制数所有位都没有 1) 。
于是区间 [ 0 , 14 ] [0,14] [ 0 , 14 ] [ ( 0000 ) 2 , ( 1000 ) 2 ) [(0000)_2,(1000)_2) [( 0000 ) 2 , ( 1000 ) 2 ) [ ( 1000 ) 2 , ( 1100 ) 2 ) [(1000)_2,(1100)_2) [( 1000 ) 2 , ( 1100 ) 2 ) [ ( 1100 ) 2 , ( 1110 ) 2 ] [(1100)_2,(1110)_2] [( 1100 ) 2 , ( 1110 ) 2 ] [ 0 , 7 ] [0,7] [ 0 , 7 ] [ 8 , 11 ] [8,11] [ 8 , 11 ] [ 12 , 14 ] [12,14] [ 12 , 14 ] [ ( 0000 ) 2 , ( 1000 ) 2 ) [(0000)_2,(1000)_2) [( 0000 ) 2 , ( 1000 ) 2 ) [ 0 , 7 ] [0,7] [ 0 , 7 ]
仍以 [ 0 , 14 ] [0,14] [ 0 , 14 ] 14 + 1 = 15 14+1=15 14 + 1 = 15 15 = ( 1111 ) 2 15=(1111)_2 15 = ( 1111 ) 2 i i i i i i k k k [ 0 , 14 ] [0,14] [ 0 , 14 ]
[ ( 1110 ) 2 , ( 1111 ) 2 ) [(1110)_2,(1111)_2) [( 1110 ) 2 , ( 1111 ) 2 ) [ 14 , 14 ] [14,14] [ 14 , 14 ] [ ( 1100 ) 2 , ( 1110 ) 2 ) [(1100)_2,(1110)_2) [( 1100 ) 2 , ( 1110 ) 2 ) [ 12 , 13 ] [12,13] [ 12 , 13 ] [ ( 1000 ) 2 , ( 1100 ) 2 ) [(1000)_2,(1100)_2) [( 1000 ) 2 , ( 1100 ) 2 ) [ 8 , 11 ] [8,11] [ 8 , 11 ] [ ( 0000 ) 2 , ( 1000 ) 2 ) [(0000)_2,(1000)_2) [( 0000 ) 2 , ( 1000 ) 2 ) [ 0 , 7 ] [0,7] [ 0 , 7 ]
利用该方法,我们一方面保证了划分动作是循环的,同时也保证了划分后的子区间是连续的,还保证了循环能够退出,即一定会完成划分。实际上经过验证后,我们发现,这样的区间划分方式完全符合前述 5 点要求,对照说明如下。
规则是固定的,因此操作是可循环的,通过这种方式,我们一定能够将 n u m s nums n u m s [ 0 , k ] [0, k] [ 0 , k ] [ 0 , k ] [0,k] [ 0 , k ] 一定有且只有一个以 k k k 。k k k n n n 0 ∼ n − 1 0 \sim n-1 0 ∼ n − 1 长度为 n n n n u m s nums n u m s n n n ,这些子区间的右界是 { 0 , 1 , 2 , . . . , n − 1 } \{0,1,2,...,n-1\} { 0 , 1 , 2 , ... , n − 1 } ( k + 1 ) − l o w b i t ( k + 1 ) (k+1)-lowbit(k+1) ( k + 1 ) − l o w bi t ( k + 1 ) { 1 − l o w b i t ( 1 ) , 2 − l o w b i t ( 2 ) , 3 − l o w b i t ( 3 ) , . . . , n − l o w b i t ( n ) } \{1-lowbit(1),2-lowbit(2),3-lowbit(3),...,n-lowbit(n)\} { 1 − l o w bi t ( 1 ) , 2 − l o w bi t ( 2 ) , 3 − l o w bi t ( 3 ) , ... , n − l o w bi t ( n )} l o w b i t ( i ) lowbit(i) l o w bi t ( i )
根据 1,对于任意的 [ l , r ] [l,r] [ l , r ] [ 0 , l − 1 ] [0,l-1] [ 0 , l − 1 ] [ 0 , r ] [0,r] [ 0 , r ] [ l , r ] [l,r] [ l , r ]
单点修改会导致所有包含被修改的元素值的区间的区间和发生变动,需要对这些区间的区间和做同样的更新操作。现在我们还不知道要怎么找 「包含给定元素的所有区间」 ,留到后续说明。
「将当前子区间右界下标最低位的 1 换成 0」的划分方式即为该规则 (即 l o w b i t ( ) lowbit() l o w bi t ( )
同 3,后续说明。
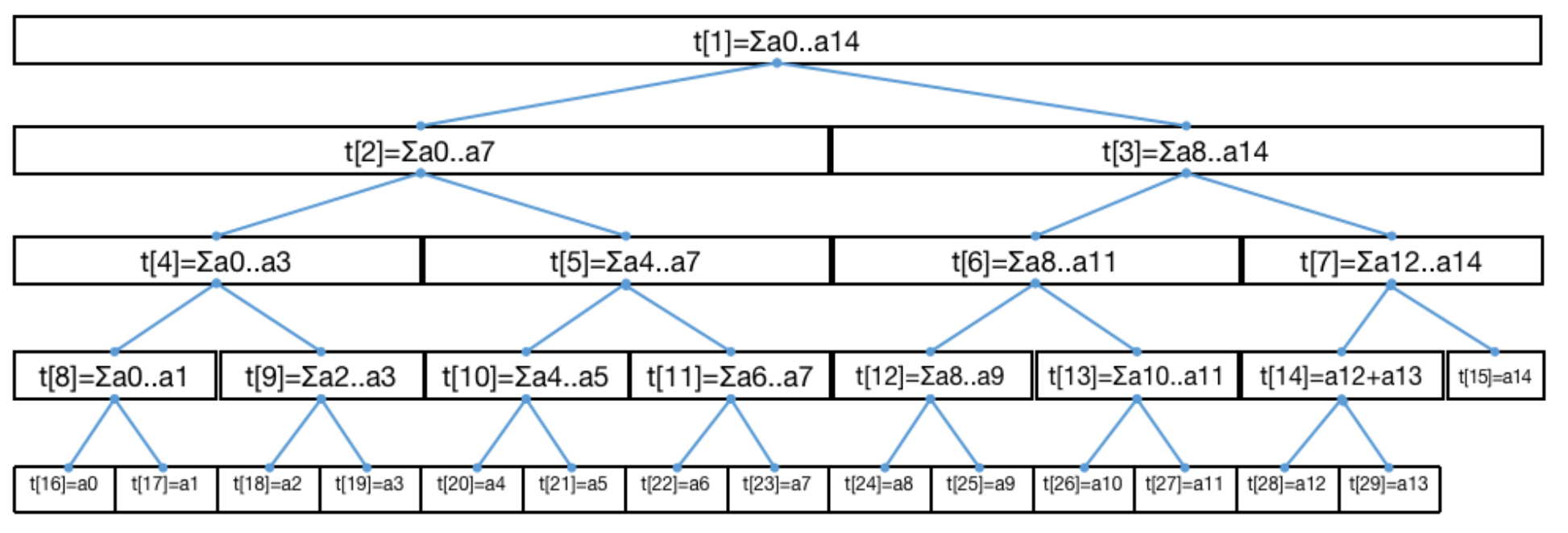
至此,我们终于可以描述「树状数组」 t r e e [ ] tree[] t ree [ ]
划分得到 n n n t r e e [ ] tree[] t ree [ ] t r e e [ 5 ] tree[5] t ree [ 5 ] n u m s [ 5 ] nums[5] n u m s [ 5 ]
由上述,t r e e tree t ree n u m s nums n u m s n n n
以 k k k ( k + 1 ) − l o w b i t ( k + 1 ) (k+1)-lowbit(k+1) ( k + 1 ) − l o w bi t ( k + 1 ) l o w b i t lowbit l o w bi t
还是很抽象?再坚持一下,介绍 l o w b i t lowbit l o w bi t
lowbit
前面我们说过「将当前子区间右界 k k k k + 1 k+1 k + 1 k + 1 k+1 k + 1 i i i
i = i & ( ∼ i + 1 ) i=i\&(\sim i+1)
i = i & ( ∼ i + 1 )
正数 i i i i = k + 1 i=k+1 i = k + 1 − i -i − i 我们知道 ,负数在计算机中以补码 (two’s complement ) 表示, 负数 − i -i − i i i i ,即 − i = ∼ i + 1 -i=\sim i+1 − i =∼ i + 1 & \& & l o w b i t ( i ) lowbit(i) l o w bi t ( i ) 该方法返回下标 i i i 。后续我们可以用该方法方便地对当前子区间右界 i i i i − l o w b i t ( i ) i-lowbit(i) i − l o w bi t ( i )
1 2 3 private int lowbit (int i) { return i & -i; }
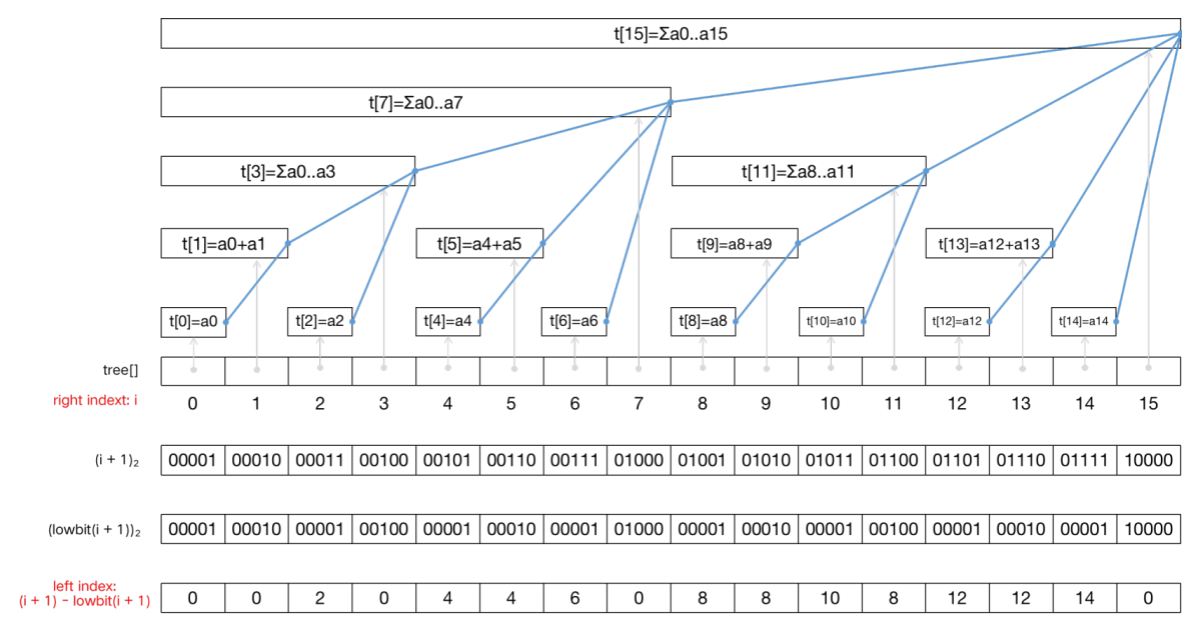
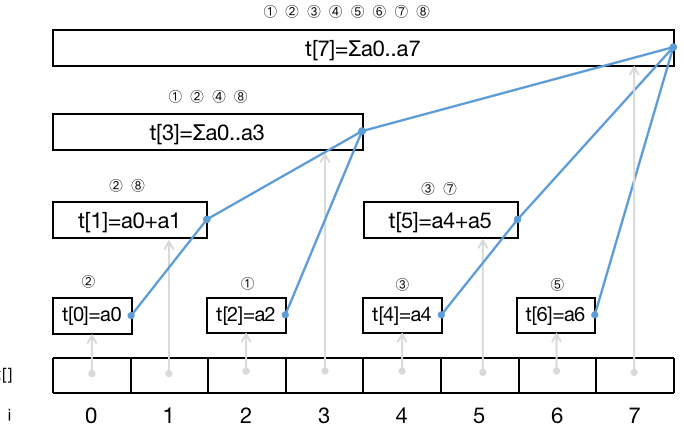
下图展示了大小为 16 的 n u m s nums n u m s a a a t [ ] t[] t [ ] t r e e [ ] tree[] t ree [ ] t r e e [ 0 ] tree[0] t ree [ 0 ] n u m s [ 0 ] nums[0] n u m s [ 0 ] t r e e [ 1 ] tree[1] t ree [ 1 ] n u m s [ 1 ] nums[1] n u m s [ 1 ] n u m s [ 0 ] nums[0] n u m s [ 0 ] n u m s [ 1 ] nums[1] n u m s [ 1 ] 区间包含关系 。单点修改操作需要更新所有包含修改点的区间的区间和,寻找包含修改点的区间的过程就是 沿着蓝线向上 的过程。
到这里,相信读者们应该对「树状数组」和 「Binary Indexed Tree 」有了更深的理解。
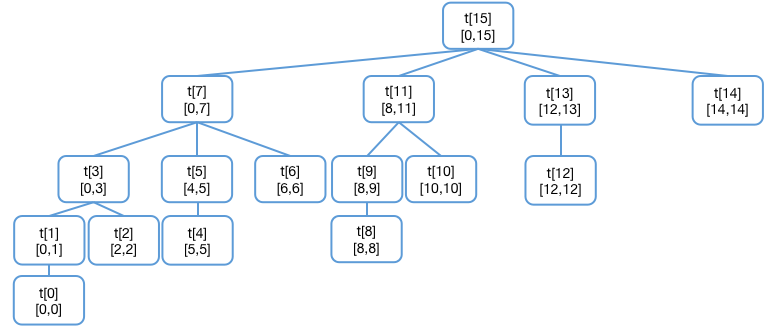
将该图稍作调整可以更清晰地看出「树」的结构。
需要强调的是,t r e e tree t ree 「二进制」表示中「二」 ,表达的是下标二进制数位取 0 或取 1 得到的下标值与 t r e e tree t ree n u m s nums n u m s n u m s nums n u m s [ 0 , 14 ] [0,14] [ 0 , 14 ] t r e e [ 7 ] tree[7] t ree [ 7 ] t r e e [ 11 ] tree[11] t ree [ 11 ] t r e e [ 13 ] tree[13] t ree [ 13 ] t r e e [ 14 ] tree[14] t ree [ 14 ]
接下来我们分析如何实现「单点修改」和「区间查询」,分析过后你会知道之前需求 3 和 5 是如何被满足的。
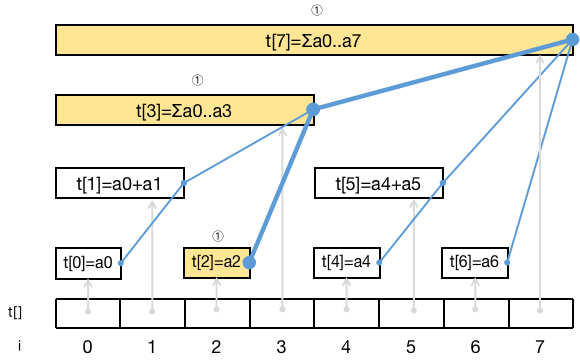
单点修改
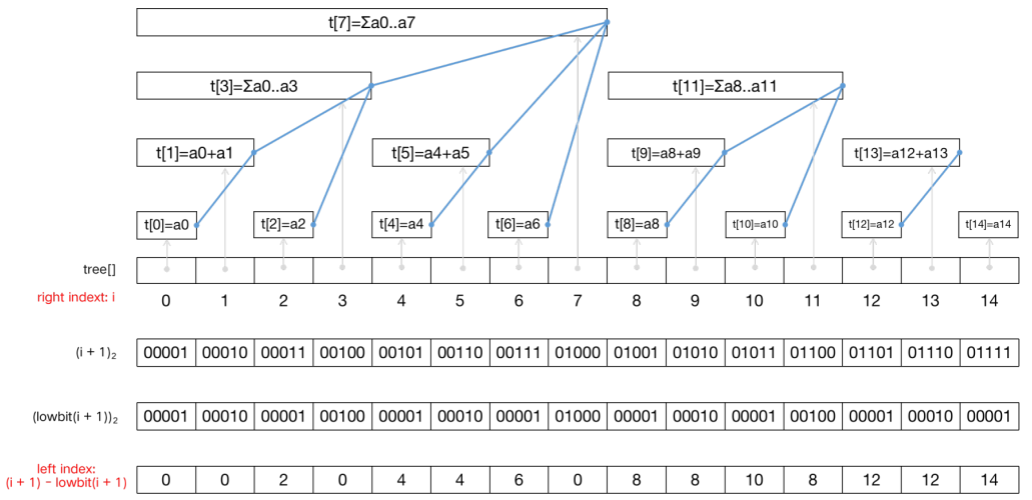
更新 n u m s [ k ] nums[k] n u m s [ k ] t r e e [ ] tree[] t ree [ ] 第一个要更新的区间和一定是 t r e e [ k ] tree[k] t ree [ k ] 。沿着蓝线上升,考虑蓝线连接的父子结点的下标二进制表示,我们发现 i = i + l o w b i t ( i ) i = i + lowbit(i) i = i + l o w bi t ( i ) i = k + 1 i=k+1 i = k + 1 i i i n − 1 n-1 n − 1 n u m s nums n u m s n n n
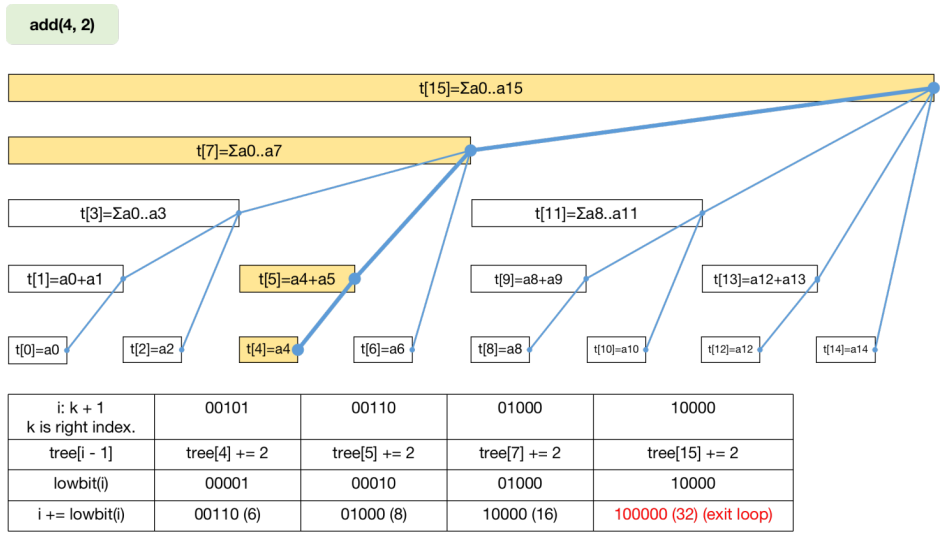
增量式单点修改方法为 public void add(int k, int x) 表示为包含 n u m s [ k ] nums[k] n u m s [ k ] x x x t r e e [ k ] tree[k] t ree [ k ] n u m s [ k ] nums[k] n u m s [ k ] x x x a d d add a dd i i i
若单点修改为覆盖式修改,则执行 public void update(int k, int x) ,表示更新 nums[k] = x ,通过调用 public void add(int k, int x) 方法实现。于是不难写出如下 u p d a t e update u p d a t e a d d add a dd l o w b i t lowbit l o w bi t
再次强调,i i i i − 1 i-1 i − 1 t r e e [ i − 1 ] tree[i-1] t ree [ i − 1 ]
1 2 3 4 5 6 7 8 9 10 11 public void update (int k, int x) { add(k, x - nums[k]); nums[k] = x; } public void add (int k, int x) { for (int i = k + 1 ; i <= n; i += lowbit(i)){ tree[i - 1 ] += x; } }
下图展示了 a d d ( 4 , 2 ) add(4,2) a dd ( 4 , 2 )
区间查询
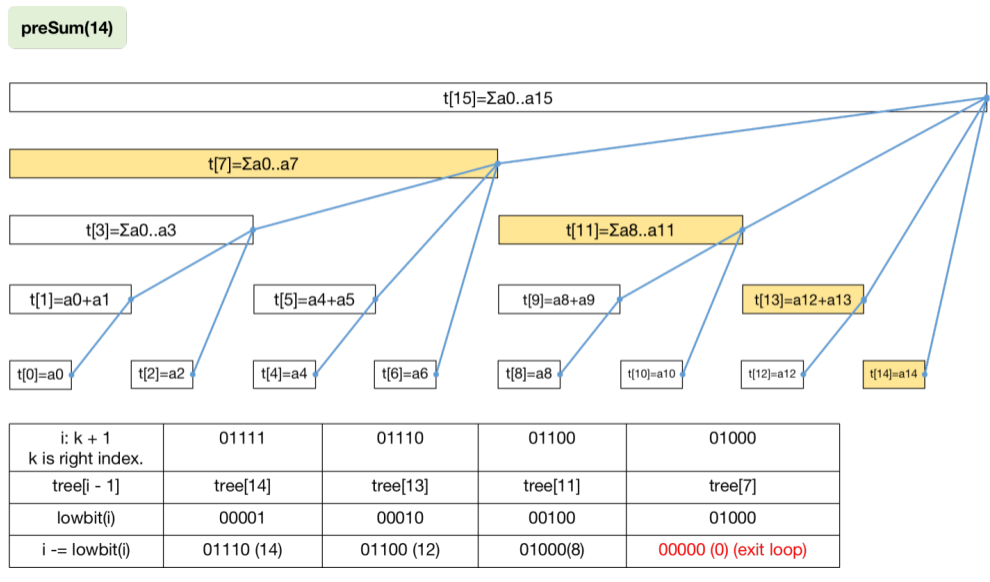
给定 n u m s nums n u m s [ l , r ] [l,r] [ l , r ] private int preSum(int k) ,表示求 n u m s [ 0 ] nums[0] n u m s [ 0 ] n u m s [ k ] nums[k] n u m s [ k ] k + 1 k+1 k + 1 [ l , r ] [l,r] [ l , r ] p r e S u m ( r ) − p r e S u m ( l − 1 ) preSum(r) - preSum(l - 1) p re S u m ( r ) − p re S u m ( l − 1 ) p r e S u m ( r ) preSum(r) p re S u m ( r ) i = i - lowbit(i) 的方式从 i = r + 1 i=r+1 i = r + 1 [ 0 , r ] [0,r] [ 0 , r ] i − 1 i-1 i − 1 t r e e tree t ree t r e e [ i − 1 ] tree[i-1] t ree [ i − 1 ] preSum(k) 方法的主体是一循环,循环条件是 i > 0 i > 0 i > 0 i = = 0 i==0 i == 0 n u m s [ 0 ] nums[0] n u m s [ 0 ] n u m s [ k ] nums[k] n u m s [ k ] s u m sum s u m p r e S u m preSum p re S u m
1 2 3 4 5 6 7 8 9 10 11 12 public int sum (int l, int r) { return preSum(r) - preSum(l - 1 ); } private int preSum (int k) { int ans = 0 ; for (int i = k + 1 ; i > 0 ; i -= lowbit(i)){ ans += tree[i - 1 ]; } return ans; }
下图展示了 p r e S u m ( 14 ) preSum(14) p re S u m ( 14 )
初始化
从「区间划分」入手,我们得出了基本树状数组所要解决的单点修改和区间查询操作,这两种操作都要建立在最初 t r e e [ ] tree[] t ree [ ] t r e e [ ] tree[] t ree [ ] t r e e [ ] tree[] t ree [ ] n u m s [ i ] nums[i] n u m s [ i ] t r e e [ i ] tree[i] t ree [ i ] a d d ( i , n u m s [ i ] ) add(i, nums[i]) a dd ( i , n u m s [ i ]) t r e e [ i ] tree[i] t ree [ i ] a d d add a dd f o r for f or t r e e [ ] tree[] t ree [ ] 任意顺序 调用 n n n a d d add a dd n n n a d d add a dd 0 ∼ n − 1 0 \sim n-1 0 ∼ n − 1 t r e e tree t ree 0 ∼ n − 1 0 \sim n-1 0 ∼ n − 1 a d d ( i , n u m s [ i ] ) add(i, nums[i]) a dd ( i , n u m s [ i ])
1 2 3 4 5 6 7 8 9 10 11 12 13 class PURQBIT { int [] nums, tree; int n; public PURQBIT (int [] nums) { this .nums = nums; this .n = nums.length; this .tree = new int [n]; for (int i = 0 ; i < n; i++){ add(i, nums[i]); } } }
时空复杂度
时间复杂度:
单点修改时间复杂度 : O ( l o g n ) O(logn) O ( l o g n )
取决于更新结点到根结点的路径上的结点数,更新 n u m s [ 0 ] ( k = 0 ) nums[0](k=0) n u m s [ 0 ] ( k = 0 ) i = k + 1 i=k+1 i = k + 1 ( 000...001 ) 2 (000...001)_2 ( 000...001 ) 2 i + = l o w b i t ( i ) i += lowbit(i) i + = l o w bi t ( i ) ( n ) 2 (n)_2 ( n ) 2 ( n ) 2 (n)_2 ( n ) 2 l o g n logn l o g n O ( l o g n ) O(logn) O ( l o g n )
区间查询时间复杂度 : O ( l o g n ) O(logn) O ( l o g n )
区间为 [ l , r ] [l, r] [ l , r ] [ 0 , l − 1 ] [0,l-1] [ 0 , l − 1 ] [ 0 , r ] [0,r] [ 0 , r ] p , q p, q p , q m a x ( p , q ) max(p,q) ma x ( p , q ) i i i i i i k k k i = k + 1 i=k+1 i = k + 1 i i i t t t i = 2 t − 1 i=2^t-1 i = 2 t − 1 t t t t = l o g ( i + 1 ) t=log(i+1) t = l o g ( i + 1 ) s u m sum s u m [ 0 , l − 1 ] [0,l-1] [ 0 , l − 1 ] [ 0 , r ] [0,r] [ 0 , r ] O ( 2 ∗ t ) O(2*t) O ( 2 ∗ t ) O ( l o g n ) O(logn) O ( l o g n )
初始化时间复杂度 : 调用 n n n a d d add a dd O ( n l o g n ) O(nlogn) O ( n l o g n )
空间复杂度: O ( n ) O(n) O ( n ) t r e e tree t ree n n n
类的实现代码
以下是「基本树状数组」 (PURQ BIT) 的实现代码,所有方法均已分析。「实战应用」中给出的 307. 区域和检索 - 数组可修改 是基本树状数组 (PURQ BIT) 模版题,利用我们给出的代码可轻松解决,详细可参考 题解 。
在这里对 t r e e tree t ree t r e e tree t ree n + 1 n+1 n + 1 t r e e [ i ] tree[i] t ree [ i ] n u m s [ i − 1 ] nums[i-1] n u m s [ i − 1 ] t r e e tree t ree n u m s nums n u m s t r e e [ i ] tree[i] t ree [ i ] n u m s [ i ] nums[i] n u m s [ i ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class PURQBIT { int [] nums, tree; int n; public PURQBIT (int [] nums) { this .nums = nums; this .n = nums.length; this .tree = new int [n]; for (int i = 0 ; i < n; i++){ add(i, nums[i]); } } public void update (int k, int x) { add(k, x - nums[k]); nums[k] = x; } public void add (int k, int x) { for (int i = k + 1 ; i <= n; i += lowbit(i)){ tree[i - 1 ] += x; } } public int sum (int l, int r) { return preSum(r) - preSum(l - 1 ); } private int preSum (int k) { int ans = 0 ; for (int i = k + 1 ; i > 0 ; i -= lowbit(i)){ ans += tree[i - 1 ]; } return ans; } private int lowbit (int i) { return i & -i; } }
RUPQ BIT (区改单查)
基本树状数组 (PURQ BIT) 很好地支持了「单点修改」及「区间查询」操作。我们进一步思考更多的区间操作,例如 「区间修改」 操作,即将指定区间的每一个元素都加上同一个值,也叫「增量式区间修改」,如果仍用基本树状数组,我们只能对区间内的每一个元素都执行一次单点修改来实现,这显然不是我们想要的。接下来我们介绍的 RUPQ BIT 引入差分数组 d i f f [ ] diff[] d i ff [ ] 「区间修改」 和 「单点查询」 操作的时间复杂度均为 O ( l o g n ) O(logn) O ( l o g n )
差分数组
「RUPQ BIT」实现的关键是 「差分数组」 。对大小为 n n n n u m s nums n u m s d i f f diff d i ff
d i f f [ 0 ] = n u m s [ 0 ] d i f f [ i ] = n u m s [ i ] − n u m s [ i − 1 ] ( i > 0 ) \begin{aligned}
diff[0] &=nums[0] \\
diff[i] &= nums[i] - nums[i - 1] (i>0)
\end{aligned}
d i ff [ 0 ] d i ff [ i ] = n u m s [ 0 ] = n u m s [ i ] − n u m s [ i − 1 ] ( i > 0 )
下面我们指出关于差分数组的重要性质。
区间修改 : [ l , r ] [l, r] [ l , r ] x x x d i f f diff d i ff d i f f [ l ] + = x diff[l] += x d i ff [ l ] + = x d i f f [ r + 1 ] − = x diff[r+1] -= x d i ff [ r + 1 ] − = x d i f f diff d i ff x x x 单点查询 : 由于我们不修改 n u m s nums n u m s O ( n ) O(n) O ( n ) n u m s nums n u m s n u m s [ k ] = ∑ i = 0 k d i f f [ i ] nums[k] = \sum_{i=0}^{k} diff[i] n u m s [ k ] = ∑ i = 0 k d i ff [ i ] d i f f [ 0 ] diff[0] d i ff [ 0 ] d i f f [ k ] diff[k] d i ff [ k ] n u m s [ k ] nums[k] n u m s [ k ]
n u m s [ k ] = ( n u m s [ k ] − n u m s [ k − 1 ] ) + ( n u m s [ k − 1 ] − n u m s [ k − 2 ] ) + . . . + ( n u m s [ 1 ] − n u m s [ 0 ] ) + n u m s [ 0 ] = d i f f [ k ] + d i f f [ k − 1 ] + . . . + d i f f [ 1 ] + d i f f [ 0 ] \begin{aligned}
nums[k] &=(nums[k]-nums[k-1])+(nums[k-1]-nums[k-2])+...+ \\
&\quad (nums[1]-nums[0])+nums[0] \\
&= diff[k]+diff[k - 1]+...+diff[1]+diff[0]
\end{aligned}
n u m s [ k ] = ( n u m s [ k ] − n u m s [ k − 1 ]) + ( n u m s [ k − 1 ] − n u m s [ k − 2 ]) + ... + ( n u m s [ 1 ] − n u m s [ 0 ]) + n u m s [ 0 ] = d i ff [ k ] + d i ff [ k − 1 ] + ... + d i ff [ 1 ] + d i ff [ 0 ]
对于「单点查询」,例如 n u m s = { 4 , 2 , − 2 , 7 , 8 } nums = \{4,2,-2,7,8\} n u m s = { 4 , 2 , − 2 , 7 , 8 } d i f f = { 4 , − 2 , − 4 , 9 , 1 } diff =\{4,-2,-4,9,1\} d i ff = { 4 , − 2 , − 4 , 9 , 1 } [ 1 , 3 ] [1,3] [ 1 , 3 ] n u m s [ 2 ] nums[2] n u m s [ 2 ]
操作
nums
diff
初始
{ 4 , 2 , − 2 , 7 , 8 } \{4,2,-2,7,8\} { 4 , 2 , − 2 , 7 , 8 } { 4 , − 2 , − 4 , 9 , 1 } \{4,-2,-4,9,1\} { 4 , − 2 , − 4 , 9 , 1 }
[ 1 , 3 ] [1,3] [ 1 , 3 ] { 4 , 5 , 1 , 10 , 8 } \{4,5,1,10,8\} { 4 , 5 , 1 , 10 , 8 } n u m s nums n u m s { 4 , 1 , − 4 , 9 , − 2 } \{4,1,-4,9,-2\} { 4 , 1 , − 4 , 9 , − 2 }
对照上表与前述分析,可以看到 d i f f [ ] diff[] d i ff [ ] d i f f [ 1 ] + = 3 diff[1]+=3 d i ff [ 1 ] + = 3 d i f f [ 4 ] − = 3 diff[4]-=3 d i ff [ 4 ] − = 3 n u m s [ 2 ] = d i f f [ 0 ] + d i f f [ 1 ] + d i f f [ 2 ] = 1 nums[2]=diff[0]+diff[1]+diff[2]=1 n u m s [ 2 ] = d i ff [ 0 ] + d i ff [ 1 ] + d i ff [ 2 ] = 1 d i f f diff d i ff n u m s nums n u m s d i f f diff d i ff 单点修改 来表达,时间复杂度为 O ( 1 ) O(1) O ( 1 ) n u m s nums n u m s d i f f diff d i ff 区间查询 (求前缀区间和) , 时间复杂度为 O ( n ) O(n) O ( n )
如果把 d i f f [ ] diff[] d i ff [ ] n u m s [ ] nums[] n u m s [ ] n u m s [ ] nums[] n u m s [ ] 区间修改 ,可通过单点修改 d i f f [ l ] diff[l] d i ff [ l ] d i f f [ r + 1 ] diff[r+1] d i ff [ r + 1 ] a d d add a dd n u m s [ ] nums[] n u m s [ ] 单点查询 则对应基本 BIT 中的求前缀和的 p r e S u m preSum p re S u m
从PURQ到RUPQ
经过前述分析,快速理解 RUPQ BIT 的关键只需明确一点: RUPQ BIT 中的 t r e e [ ] tree[] t ree [ ] d i f f [ ] diff[] d i ff [ ]
PURQ BIT
RUPQ BIT
输入数组
n u m s [ ] nums[] n u m s [ ] n u m s [ ] nums[] n u m s [ ]
前缀和求解对象
n u m s [ ] nums[] n u m s [ ] d i f f [ ] diff[] d i ff [ ]
逻辑二元索引树
n u m s [ ] nums[] n u m s [ ] t r e e [ ] tree[] t ree [ ] d i f f [ ] diff[] d i ff [ ] t r e e [ ] tree[] t ree [ ]
通过「差分数组」的学习,我们知道 RUPQ BIT 的「区间修改」,实际上只需要执行 a d d ( l , x ) add(l, x) a dd ( l , x ) a d d ( r + 1 , − x ) add(r+1,-x) a dd ( r + 1 , − x ) a d d add a dd f o r for f or p r e S u m ( k ) preSum(k) p re S u m ( k ) d i f f [ 0 ] ∼ d i f f [ k ] diff[0] \sim diff[k] d i ff [ 0 ] ∼ d i ff [ k ] n u m s [ k ] nums[k] n u m s [ k ] n u m s nums n u m s d i f f diff d i ff a d d add a dd q u e r y query q u ery
时空复杂度
分析方法及结果均同 PURQ BIT。
类的代码实现
以下是 RUPQ BIT 的实现代码。「实战应用」中给出的 307. 区域和检索 - 数组可修改 虽是基本树状数组 (PURQ BIT) 模版题,但我们也可以用 RUPQ BIT 解决。用左右界相同的区间修改来实现单点修改,对区间大小为 k k k k k k O ( n l o g n ) O(nlogn) O ( n l o g n ) n u m s nums n u m s k k k 题解 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class RUPQBIT { int [] diff, tree; int n; public RUPQBIT (int [] nums) { this .n = nums.length; this .diff = new int [n]; this .tree = new int [n]; diff[0 ] = nums[0 ]; for (int i = 1 ; i < n; i++){ diff[i] = nums[i] - nums[i - 1 ]; } for (int i = 0 ; i < n; i++){ add(i, diff[i]); } } public void update (int l, int r, int x) { add(l, x); add(r + 1 , -x); } public int query (int k) { return preSum(k); } private void add (int k, int x) { for (int i = k + 1 ; i <= n; i += lowbit(i)){ tree[i - 1 ] += x; } } private int preSum (int k) { int ans = 0 ; for (int i = k + 1 ; i > 0 ; i -= lowbit(i)){ ans += tree[i - 1 ]; } return ans; } private int lowbit (int i) { return i & -i; } }
我们已经有了 PURQ BIT ,因此 RUPQ BIT 可以十分简单地调用前者的方法即可,所以 RUPQ BIT 类也可以这么写。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class RUPQBIT2 { private PURQBIT purqBit; public RUPQBIT2 (int [] nums) { int [] diff = new int [nums.length]; diff[0 ] = nums[0 ]; for (int i = 1 ; i < nums.length; i++){ diff[i] = nums[i] - nums[i - 1 ]; } this .purqBit = new PURQBIT (diff); } public void update (int l, int r, int x) { purqBit.add(l, x); purqBit.add(r + 1 , -x); } public int query (int k) { return purqBit.sum(0 , k); } }
RURQ BIT (区改区查)
本小节介绍第三种树状数组,RURQ BIT ,即 「区间修改区间查询」树状数组 。RURQ BIT 以 O ( l o g n ) O(logn) O ( l o g n ) 「区间修改」 及 「区间查询」 。
从RUPQ到RURQ
该版本的 BIT 在 RUPQ BIT 差分数组的基础上, 通过如下算式推导发现只需 再引入一棵逻辑树 即可同时以 O ( l o g n ) O(logn) O ( l o g n ) 「区间修改」 及 「区间查询」 。
s u m ( l , r ) = p r e S u m ( r ) − p r e S u m ( l − 1 ) = ( n u m s [ 0 ] + n u m s [ 1 ] + , . . . , + n u m s [ r ] ) − ( n u m s [ 0 ] + n u m s [ 1 ] + . . . + n u m s [ l − 1 ] ) \begin{aligned}
sum(l,r) &= preSum(r)-preSum(l-1) \\
&= (nums[0]+nums[1]+,...,+nums[r])-(nums[0]+nums[1]+...+nums[l-1]) \\
\end{aligned}
s u m ( l , r ) = p re S u m ( r ) − p re S u m ( l − 1 ) = ( n u m s [ 0 ] + n u m s [ 1 ] + , ... , + n u m s [ r ]) − ( n u m s [ 0 ] + n u m s [ 1 ] + ... + n u m s [ l − 1 ])
p r e S u m ( k ) = n u m s [ 0 ] + n u m s [ 1 ] + , . . . , + n u m s [ k ] = d i f f [ 0 ] + ( d i f f [ 0 ] + d i f f [ 1 ] ) + , . . . , + ( d i f f [ 0 ] + d i f f [ 1 ] + , . . . , + d i f f [ k ] ) = ( k + 1 ) ∗ d i f f [ 0 ] + k ∗ d i f f [ 1 ] + , . . . , + d i f f [ k ] = ( k + 1 ) ∗ ( d i f f [ 0 ] + d i f f [ 1 ] + , . . . , + d i f f [ k ] ) − ( 0 ∗ d i f f [ 0 ] + 1 ∗ d i f f [ 1 ] + , . . . , + k ∗ d i f f [ k ] ) \begin{aligned}
preSum(k)&=nums[0]+nums[1]+,...,+nums[k] \\
&=diff[0]+(diff[0]+diff[1])+,...,+(diff[0]+diff[1]+,...,+diff[k])\\
&=(k+1)*diff[0]+k*diff[1]+,...,+diff[k] \\
&=(k+1)*(diff[0]+diff[1]+,...,+diff[k])\\
&\quad -(0*diff[0]+1*diff[1]+,...,+k*diff[k])
\end{aligned}
p re S u m ( k ) = n u m s [ 0 ] + n u m s [ 1 ] + , ... , + n u m s [ k ] = d i ff [ 0 ] + ( d i ff [ 0 ] + d i ff [ 1 ]) + , ... , + ( d i ff [ 0 ] + d i ff [ 1 ] + , ... , + d i ff [ k ]) = ( k + 1 ) ∗ d i ff [ 0 ] + k ∗ d i ff [ 1 ] + , ... , + d i ff [ k ] = ( k + 1 ) ∗ ( d i ff [ 0 ] + d i ff [ 1 ] + , ... , + d i ff [ k ]) − ( 0 ∗ d i ff [ 0 ] + 1 ∗ d i ff [ 1 ] + , ... , + k ∗ d i ff [ k ])
从 p r e S u m ( k ) preSum(k) p re S u m ( k ) k + 1 k+1 k + 1 p r e S u m ( k ) preSum(k) p re S u m ( k ) h e l p e r T r e e helperTree h e lp er T ree h e l p e r A r r = { i ∗ d i f f [ i ] } , i ∈ [ 0 , n − 1 ] helperArr=\{i*diff[i]\}, i∈[0,n-1] h e lp er A rr = { i ∗ d i ff [ i ]} , i ∈ [ 0 , n − 1 ] t r e e , h e l p e r T r e e tree, helperTree t ree , h e lp er T ree
时空复杂度
分析方法及结果类似 PURQ BIT。
类的实现代码
以下是 RURQ BIT 的实现代码。「实战应用」中给出的 307. 区域和检索 - 数组可修改 虽是基本树状数组 (PURQ BIT) 模版题,但我们也可以用 RURQ BIT 解决。其中,单点修改用左右界相同的区间修改来实现,通过 RURQ BIT 实现的 PU / RQ 操作的时间复杂度也都是 O ( l o g n ) O(logn) O ( l o g n ) 题解 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 class RURQBIT { int [] diff, tree, helperTree; int n; public RURQBIT (int [] nums) { this .n = nums.length; this .diff = new int [n]; this .tree = new int [n]; this .helperTree = new int [n]; diff[0 ] = nums[0 ]; for (int i = 1 ; i < n; i++){ diff[i] = nums[i] - nums[i - 1 ]; } for (int i = 0 ; i < n; i++){ add(tree, i, diff[i]); add(helperTree, i, i * diff[i]); } } public void update (int l, int r, int x) { add(tree, l, x); add(tree, r + 1 , -x); add(helperTree, l, l * x); add(helperTree, r + 1 , (r + 1 ) * (-x)); } public int sum (int l, int r) { int preSumLeft = l * preSum(tree, l - 1 ) - preSum(helperTree, l - 1 ); int preSumRight = (r + 1 ) * preSum(tree, r) - preSum(helperTree, r); return preSumRight - preSumLeft; } public int preSum (int [] thisTree, int k) { int ans = 0 ; for (int i = k + 1 ; i > 0 ; i -= lowbit(i)){ ans += thisTree[i - 1 ]; } return ans; } private void add (int [] thisTree, int k, int x) { for (int i = k + 1 ; i <= n; i += lowbit(i)){ thisTree[i - 1 ] += x; } } private int lowbit (int i) { return i & -i; } }
离散化
对于区间问题,当我们只关心输入数组 n u m s nums n u m s n u m s nums n u m s s e t set se t 「紧离散」 ;另一种则没有去重,因此离散化后的有效数字更多 (存在相同的数字),取值范围也更大,我称之为 「松离散」 。以下是两种离散化方式的实现。
松离散
1 2 3 4 5 6 7 8 9 10 private void discrete (int [] nums) { int n = nums.length; int [] tmp = new int [n]; System.arraycopy(nums, 0 , tmp, 0 , n); Arrays.sort(tmp); for (int i = 0 ; i < n; ++i) { nums[i] = Arrays.binarySearch(tmp, nums[i]) + 1 ; } }
紧离散
1 2 3 4 5 6 7 8 9 10 11 private Map<Integer, Integer> discrete (int [] nums) { Map<Integer, Integer> map = new HashMap <>(); Set<Integer> set = new HashSet <>(); for (int num : nums) set.add(num); List<Integer> list = new ArrayList <>(set); Collections.sort(list); int idx = 0 ; for (int num : list) map.put(num, ++idx); return map; }
例如对于 n u m s = { 2 , 4 , 4 , 6 } nums=\{2,4,4,6\} n u m s = { 2 , 4 , 4 , 6 } n u m s = { 1 , 2 , 2 , 4 } nums=\{1,2,2,4\} n u m s = { 1 , 2 , 2 , 4 } n u m s nums n u m s m a p = { ( 2 , 1 ) , ( 4 , 2 ) , ( 6 , 3 ) } map=\{(2,1),(4,2),(6,3)\} ma p = {( 2 , 1 ) , ( 4 , 2 ) , ( 6 , 3 )} k e y key k ey n u m s nums n u m s v a l u e value v a l u e v a l u e value v a l u e m a p map ma p 327. 区间和的个数 和 493. 翻转对 )。
指定区间内指定取值范围的元素数
下面我们重点介绍巧用树状数组解决的一类常见问题 ── 求指定区间 [ l , r ] [l,r] [ l , r ] [ l o w e r , u p p e r ] [lower, upper] [ l o w er , u pp er ] 。
有点拗口?没关系,我们先从著名的 「逆序对」 问题开始。 剑指 Offer 51. 数组中的逆序对 一题,求输入数组 n u m s nums n u m s 是树状数组的经典应用,更是一个「妙用」 。我们指出,它属于本节标题「指定区间指定取值范围的元素数」的范畴。
但在讨论树状数组解法之前,我们先给出最朴素两层循环做法 (该做法有许多不同的写法,这里选取一种与我们树状数组解法最为对应的写法)。
外层循环遍历 n u m s nums n u m s n u m s [ i ] nums[i] n u m s [ i ] 顺序遍历 n u m s [ j ] ( j > i ) nums[j](j>i) n u m s [ j ] ( j > i ) n u m s [ i ] > n u m s [ j ] nums[i]>nums[j] n u m s [ i ] > n u m s [ j ] ( n u m s [ i ] , n u m [ j ] ) (nums[i],num[j]) ( n u m s [ i ] , n u m [ j ]) c o u n t G r e a t e r [ j ] + + countGreater[j]++ co u n tG re a t er [ j ] + + c o u n t G r e a t e r [ j ] countGreater[j] co u n tG re a t er [ j ] n u m s [ j ] nums[j] n u m s [ j ]
当程序结束时,每一个 c o u n t G r e a t e r [ i ] countGreater[i] co u n tG re a t er [ i ] n u m s [ i ] nums[i] n u m s [ i ] ( x , n u m s [ i ] ) , x > n u m s [ i ] (x,nums[i]),x>nums[i] ( x , n u m s [ i ]) , x > n u m s [ i ] x x x n u m s [ i ] nums[i] n u m s [ i ] c o u n t G r e a t e r [ i ] countGreater[i] co u n tG re a t er [ i ] n u m s nums n u m s c o u n t G r e a t e r [ i ] countGreater[i] co u n tG re a t er [ i ] n u m s [ i − 1 ] nums[i-1] n u m s [ i − 1 ] n u m s [ i ] nums[i] n u m s [ i ]
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int reversePairs (int [] nums) { int n = nums.length, ans = 0 ; int [] countGreater = new int [n]; for (int i = 0 ; i < n; i++){ ans += countGreater[i]; for (int j = i + 1 ; j < n; j++){ if (nums[i] > nums[j]) countGreater[j]++; } } return ans; } }
我们再回到树状数组的做法,如下。其中的 d i s c r e t e discrete d i scre t e 题解 )。
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int reversePairs (int [] nums) { discrete(nums); BIT bit = new BIT (nums); int n = nums.length, ans = 0 ; for (int i = n - 1 ; i >= 0 ; --i) { ans += bit.preSum((nums[i] - 1 ) - 1 ); bit.add(nums[i] - 1 , 1 ); } return ans; } }
在主方法 r e v e r s e P a i r s reversePairs re v erse P ai rs n u m s nums n u m s n u m s nums n u m s n u m s nums n u m s 逆序遍历 n u m s nums n u m s n u m s [ i ] nums[i] n u m s [ i ] p r e S u m preSum p re S u m a d d add a dd p r e S u m ( k ) preSum(k) p re S u m ( k ) k + 1 k+1 k + 1 a d d ( k , x ) add(k,x) a dd ( k , x ) k k k x x x a d d ( n u m s [ i ] − 1 , 1 ) add(nums[i]-1,1) a dd ( n u m s [ i ] − 1 , 1 ) a d d ( n u m s [ i ] − 1 , 1 ) add(nums[i]-1,1) a dd ( n u m s [ i ] − 1 , 1 )
该方法使得 t r e e tree t ree t r e e [ n u m s [ i ] − 1 ] tree[nums[i]-1] t ree [ n u m s [ i ] − 1 ] n u m s [ i ] − 1 nums[i]-1 n u m s [ i ] − 1 x x x t r e e [ x ] tree[x] t ree [ x ] t r e e tree t ree [ 0 , n − 1 ] [0,n-1] [ 0 , n − 1 ] n u m s nums n u m s [ 1 , n ] [1,n] [ 1 , n ] 一一对应 ,可以把 a d d add a dd p r e S u m preSum p re S u m n u m s [ i ] − 1 nums[i]-1 n u m s [ i ] − 1 n u m s [ i ] nums[i] n u m s [ i ] t r e e [ i ] tree[i] t ree [ i ]
举例说明。假设松离散化后有 n u m s = { 2 , 6 , 8 , 7 , 4 , 5 , 1 , 3 } nums = \{2,6,8,7,4,5,1,3\} n u m s = { 2 , 6 , 8 , 7 , 4 , 5 , 1 , 3 } n u m s [ i ] nums[i] n u m s [ i ] a d d ( n u m s [ i ] − 1 , 1 ) add(nums[i]-1,1) a dd ( n u m s [ i ] − 1 , 1 ) n u m s [ 7 ] = 3 nums[7]=3 n u m s [ 7 ] = 3 a d d ( 2 , 1 ) add(2, 1) a dd ( 2 , 1 )
a d d add a dd t r e e [ 2 ] tree[2] t ree [ 2 ] t r e e [ 3 ] tree[3] t ree [ 3 ] t r e e [ 7 ] tree[7] t ree [ 7 ] 大于等于 n u m s [ 7 ] nums[7] n u m s [ 7 ] n u m s [ j ] nums[j] n u m s [ j ] c o u n t G r e a t e r E q u a l [ j ] + + countGreaterEqual[j]++ co u n tG re a t er Eq u a l [ j ] + + c o u n t G r e a t e r E q u a l countGreaterEqual co u n tG re a t er Eq u a l C o u n t e r G r e a t e r CounterGreater C o u n t er G re a t er c o u n t G r e a t e r E q u a l [ j ] countGreaterEqual[j] co u n tG re a t er Eq u a l [ j ] p r e S u m preSum p re S u m
由于我们从后往前求逆序对,因此我们考察左侧元素 n u m s [ j ] nums[j] n u m s [ j ] c o u n t G r e a t e r E q u a l [ j ] countGreaterEqual[j] co u n tG re a t er Eq u a l [ j ] p r e S u m ( n u m s [ j ] − 1 ) preSum(nums[j]-1) p re S u m ( n u m s [ j ] − 1 )
1 2 3 4 5 6 7 preSum(nums[6] - 1) = preSum[0] = 0 preSum(nums[5] - 1) = preSum[4] = 1 preSum(nums[4] - 1) = preSum[3] = 1 preSum(nums[3] - 1) = preSum[6] = 1 preSum(nums[2] - 1) = preSum[7] = 1 preSum(nums[1] - 1) = preSum[5] = 1 preSum(nums[0] - 1) = preSum[1] = 0
所以本质上 a d d ( n u m s [ i ] − 1 , 1 ) add(nums[i]-1,1) a dd ( n u m s [ i ] − 1 , 1 ) n u m s nums n u m s 大于等于 n u m s [ i ] nums[i] n u m s [ i ] n u m s [ j ] nums[j] n u m s [ j ] c o u n t G r e a t e r E q u a l [ j ] countGreaterEqual[j] co u n tG re a t er Eq u a l [ j ] c o u n t e r G r e a t e r E q u a l [ j ] counterGreaterEqual[j] co u n t er G re a t er Eq u a l [ j ] p r e S u m ( n u m s [ j ] − 1 ) preSum(nums[j]-1) p re S u m ( n u m s [ j ] − 1 ) n u m s [ i ] nums[i] n u m s [ i ] ( n u m s [ i ] , x ) (nums[i], x) ( n u m s [ i ] , x ) x x x n u m s [ i ] nums[i] n u m s [ i ] a d d [ n u m s [ i − 1 ] − 1 , 1 ] add[nums[i-1] - 1, 1] a dd [ n u m s [ i − 1 ] − 1 , 1 ] p r e S u m preSum p re S u m
需要注意的是,当我们执行 p r e S u m ( n u m s [ i ] − 1 ) preSum(nums[i]-1) p re S u m ( n u m s [ i ] − 1 ) { ( n u m s [ i ] , x ) , n u m s [ i ] ≥ x } \{(nums[i],x), nums[i]≥x\} {( n u m s [ i ] , x ) , n u m s [ i ] ≥ x } c o u n t e r G r e a t e r E q u a l [ i ] counterGreaterEqual[i] co u n t er G re a t er Eq u a l [ i ] { ( n u m s [ i ] , x ) , n u m s [ i ] > x } \{(nums[i],x), nums[i]>x\} {( n u m s [ i ] , x ) , n u m s [ i ] > x } c o u n t e r G r e a t e r [ i ] counterGreater[i] co u n t er G re a t er [ i ] p r e S u m ( 6 ) preSum(6) p re S u m ( 6 ) t r e e [ 6 ] + t r e e [ 5 ] + t r e e [ 3 ] tree[6]+tree[5]+tree[3] t ree [ 6 ] + t ree [ 5 ] + t ree [ 3 ] t r e e [ 6 ] tree[6] t ree [ 6 ] p r e S u m ( 5 ) preSum(5) p re S u m ( 5 ) p r e S u m ( ( n u m s [ i ] − 1 ) − 1 ) preSum((nums[i]-1)-1) p re S u m (( n u m s [ i ] − 1 ) − 1 ) p r e S u m ( n u m s [ i ] − 2 ) preSum(nums[i]-2) p re S u m ( n u m s [ i ] − 2 ) c o u n t e r G r e a t e r [ i ] counterGreater[i] co u n t er G re a t er [ i ]
现在我们将树状数组解法与朴素解法对比如下。
操作
朴素解法
树状数组解法
累计当前元素的逆序数
ans += countGreater[i];( x , n u m s [ i ] ) , x > n u m s [ i ] (x,nums[i]),x>nums[i] ( x , n u m s [ i ]) , x > n u m s [ i ] ans += bit.preSum(nums[i] - 2);( n u m s [ i ] , x ) , n u m s [ i ] > x (nums[i],x),nums[i]>x ( n u m s [ i ] , x ) , n u m s [ i ] > x
计算当前元素的逆序数
内层循环( n u m s [ i ] , x ) , n u m s [ i ] > x (nums[i],x),nums[i]>x ( n u m s [ i ] , x ) , n u m s [ i ] > x
bit.add(nums[i] - 1, 1);( x , n u m s [ i ] ) , x > n u m s [ i ] (x,nums[i]),x>nums[i] ( x , n u m s [ i ]) , x > n u m s [ i ]
我们惊讶地发现,a d d add a dd O ( l o g n ) O(logn) O ( l o g n ) n u m s [ i ] nums[i] n u m s [ i ] n u m s [ i ] nums[i] n u m s [ i ] n u m s [ j ] ( j > i ) nums[j] (j>i) n u m s [ j ] ( j > i ) c o u n t G r e a t e r [ j ] countGreater[j] co u n tG re a t er [ j ] a d d add a dd n u m s [ i ] nums[i] n u m s [ i ] n u m s [ j ] nums[j] n u m s [ j ] c o u n t G r e a t e r E q u a l [ j ] countGreaterEqual[j] co u n tG re a t er Eq u a l [ j ] p r e S u m ( n u m [ j ] − 1 ) preSum(num[j]-1) p re S u m ( n u m [ j ] − 1 ) n u m s [ i ] nums[i] n u m s [ i ] n u m s [ i ] nums[i] n u m s [ i ] n u m s [ i ] nums[i] n u m s [ i ] a d d add a dd n u m s [ i ] nums[i] n u m s [ i ] n u m s [ i ] nums[i] n u m s [ i ]
总之,我们将一个 n u m s nums n u m s p r e S u m ( n u m s [ i ] − 2 ) preSum(nums[i]-2) p re S u m ( n u m s [ i ] − 2 ) { ( n u m s [ i ] , x ) , n u m s [ i ] > x } \{(nums[i],x),nums[i]>x\} {( n u m s [ i ] , x ) , n u m s [ i ] > x } a d d ( n u m s [ i ] − 1 , 1 ) add(nums[i]-1, 1) a dd ( n u m s [ i ] − 1 , 1 ) { ( x , n u m s [ i ] ) , x > n u m s [ i ] } \{(x,nums[i]),x>nums[i]\} {( x , n u m s [ i ]) , x > n u m s [ i ]} t r e e [ ] tree[] t ree [ ]
实际上 p r e S u m ( ( [ n u m s [ i ] − 1 ) − 1 ] ) preSum(([nums[i]-1)-1]) p re S u m (([ n u m s [ i ] − 1 ) − 1 ]) p r e S u m ( ( n u m s [ i ] − 1 ) − 1 ) preSum((nums[i]-1)-1) p re S u m (( n u m s [ i ] − 1 ) − 1 ) [ i + 1 , n − 1 ] [i+1,n-1] [ i + 1 , n − 1 ] [ 1 , n u m s [ i ] − 1 ] [1,nums[i]-1] [ 1 , n u m s [ i ] − 1 ] { ( n u m s [ i ] , n u m s [ j ] ) , j ∈ [ i + 1 , n − 1 ] } \{(nums[i],nums[j]),j∈[i+1,n-1]\} {( n u m s [ i ] , n u m s [ j ]) , j ∈ [ i + 1 , n − 1 ]}
对于前面的例子 n u m s = { 2 , 6 , 8 , 7 , 4 , 5 , 1 , 3 } nums = \{2,6,8,7,4,5,1,3\} n u m s = { 2 , 6 , 8 , 7 , 4 , 5 , 1 , 3 }
1 2 3 4 5 6 7 8 ① add(2, 1) ② add(0, 1) ③ add(4, 1) ④ add(3, 1) ⑤ add(6, 1) ⑥ add(7, 1) ⑦ add(5, 1) ⑧ add(1, 1)
在理解了「遍历离散化后的 n u m s nums n u m s p r e S u m preSum p re S u m a d d add a dd
315. 计算右侧小于当前元素的个数 题,与「逆序数」问题的区别仅在此题要求解「小于」,逆序数问题中涉及的是「小于等于」,只需要在「小于等于」版本的代码上做简单调整即可,详情见题解。406. 根据身高重建队列 也是用树状数组求对于当前元素它之前的「小于等于」它的元素个数的问题,具体实现需结合二分查找,这是树状数组与其他方法相结合的一个好例子。493. 翻转对 。「逆序对」的变形题,q u e r y ( x ) query(x) q u ery ( x ) x x x n u m s nums n u m s n u m s nums n u m s 327. 区间和的个数 。此题是更进阶的题目,不仅求解对象从 n u m s nums n u m s p r e S u m s preSums p re S u m s l o w e r , u p p e r lower, upper l o w er , u pp er [ 1 , n ] [1,n] [ 1 , n ] n n n n u m s nums n u m s
不得不说树状数组的这个应用确实十分抽象,希望读者仔细阅读本节内容后能够完全理解。关于这几题的详细题解和更多的树状数组题目,请参考「实战应用」。
总结
关于「树状数组」,总结本文内容如下。
基本的树状数组 (PURQ BIT) 以 O ( l o g n ) O(logn) O ( l o g n ) n n n 单点修改 及 区间查询 问题。
我们从区间查询出发,思考如何利用类似倍增思想的做法来划分子区间,从而提高区间查询的效率。
通过对 n u m s nums n u m s n n n 「二元索引树」 。
单点修改及区间查询的时间复杂度都与 ( n ) 2 (n)_2 ( n ) 2 O ( l o g n ) O(logn) O ( l o g n )
在 PURQ BIT 的基础上,引入 差分数组 ,实现了 RUPQ BIT。
在 RUPQ BIT 的基础上,根据 算式推导 ,引入 辅助树状数组 ,实现了 RURQ BIT。
当区间问题只关心元素之间的大小关系而不关心元素值时,可以先将输入序列 离散化 ,有助于提高求解效率或帮助解决一些特定问题。离散化实现包括 松离散 和 紧离散 。
「求指定区间 [ l , r ] [l,r] [ l , r ] [ l o w e r , u p p e r ] [lower, upper] [ l o w er , u pp er ]
总结不同方式的 PU/PQ/RU/RQ 操作的时间复杂度如下。
方式
单点修改
单点查询
区间修改
区间查询
普通数组
O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( n ) O(n) O ( n )
普通数组+前缀和数组
O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 )
差分数组
O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n )
PURQ BIT
★ O ( l o g n ) O(logn) O ( l o g n )
★ O ( l o g n ) O(logn) O ( l o g n )
RUPQ BIT
★ O ( l o g n ) O(logn) O ( l o g n )
★ O ( l o g n ) O(logn) O ( l o g n )
RURQ BIT
★ O ( l o g n ) O(logn) O ( l o g n )
★ O ( l o g n ) O(logn) O ( l o g n )
值得注意的是,RURQ BIT 对大小为1的区间执行区间修改和区间查询实际上就是单点修改和单点查询,因此 RURQ BIT 以 O ( l o g n ) O(logn) O ( l o g n )
实战应用
【文章更新日志】
[2022-10-03]
[2022-09-23]
[2022-07-25]