Dijkstra算法正确性证明

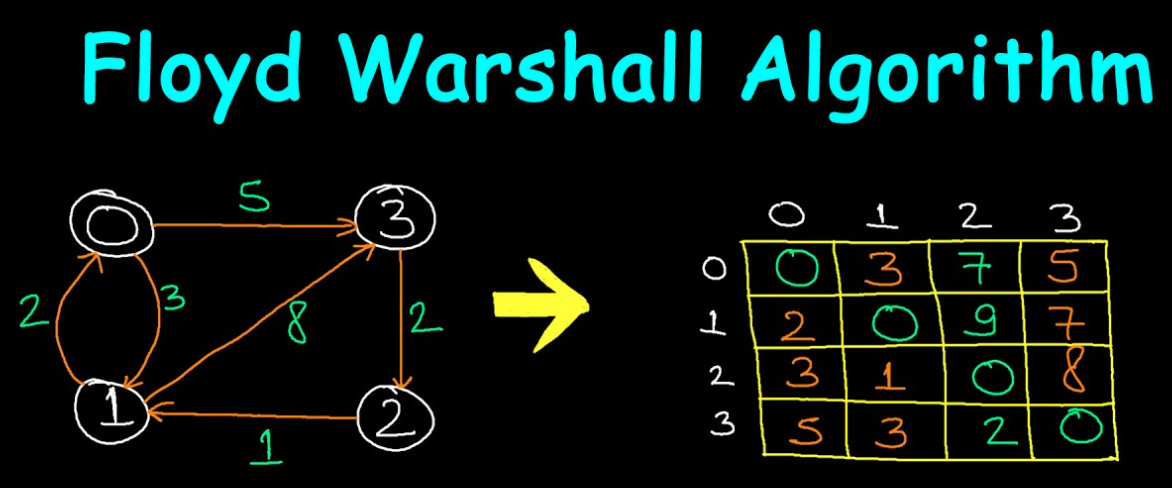
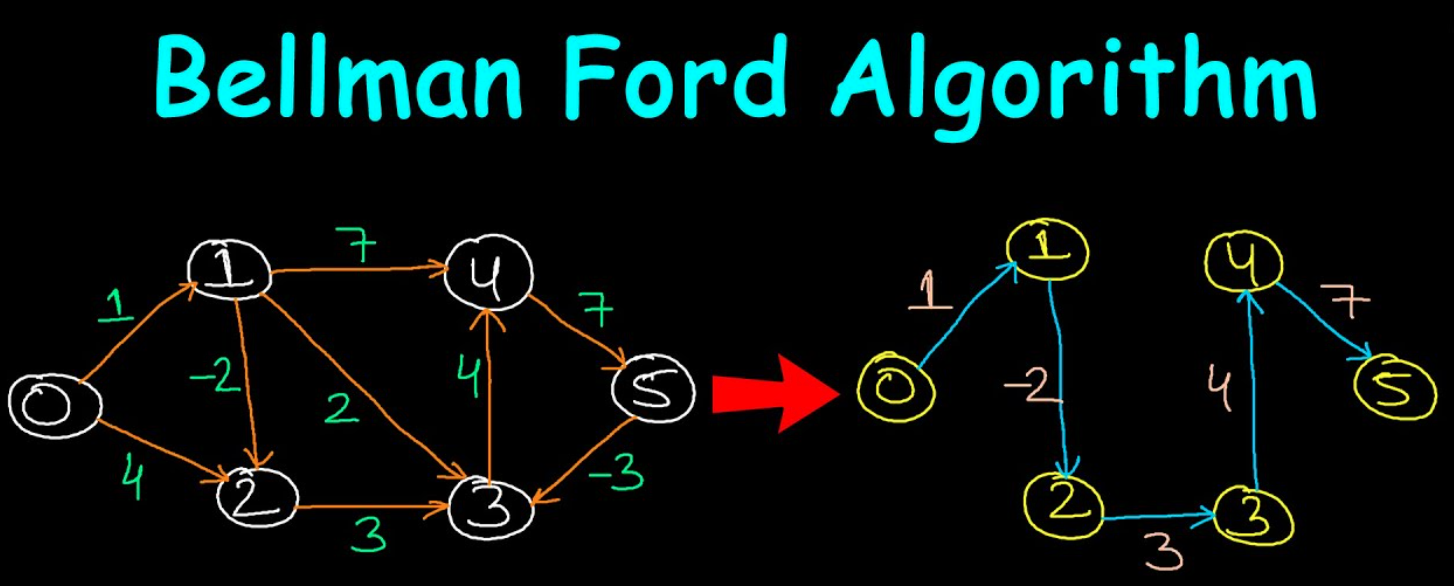
算法描述

Dijkstra算法(狄杰斯特拉算法)：
一种基于广度优先搜索和贪婪思想的求解 无负边有向赋权图单源最短路径 的算法。
算法将所有顶点区分为「到源点 $s$ 的最短距离」(以后简称「距离」) 已确定 和 未确定 的顶点。算法开始前所有顶点的距离均未确定(一般置为 $Infinity$ )，初始时置 $s$ 的距离为 0。以一个while循环查询当前 是否有距离未确定 的顶点，若有则将其中距离最小者 $v$ 选为 当前顶点，并使其距离已知。然后以BFS的方式松弛 $v$ 的邻接顶点 $w$ 并更新 $w$ 的前驱为 $v$ 。当不再有未确定距离的顶点时算法结束，此时每一个顶点的距离均最小。通过递归寻找节点的前驱可以得到 $s$ 到该顶点的具体的最短路径。

松弛操作 是最短路径算法的关键，在确定当前顶点 $v$ (最新成为已确定距离的顶点) 后立即操作，目的是更新 $v$ 的邻接顶点 $w$ 的距离和其前驱。如下图， $s$ 经过若干个顶点到 $a$ 和 $b$ ， $a$ 和 $b$ 邻接 $c$ 。假设此时 $dw = Inifinity$ ， $da = 5$ ， $db = 10$ 。

$a$ 先于 $b$ 成为当前顶点，由于 $da + |(a, w)| = 15 < Infinity$ ，故 $a$ 松弛 $dw$ ，并将 $w$ 的前驱置为 $a$ ， $w.pre = a$ 。

$b$ 成为当前顶点时，由于 $db + |(b, w)| = 11 < 15$ ，故 $b$ 松弛 $dw$ ，并将 $w$ 的前驱置为 $b$ ， $w.pre = b$ 。

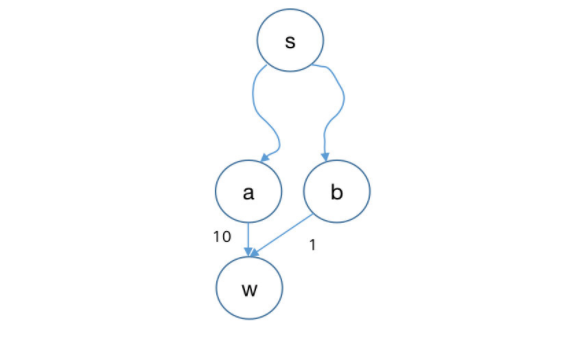
一个直观的观察是，来自 $w$ 入边的松弛，使得 $dw$ 不断更新至所有可能的路径距离的最小值。以下严格证明该算法正确性。

算法正确性证明

利用数学归纳法(结合反证法)证明。

本证明参考了这个帖子。

a) 数学归纳法的证明过程

起始验证。对于命题 $P(n)$ ，当 $n = 1$ 时命题 $P$ 成立。
假设命题成立。假设命题 $P(n)$ 在 $n = m (m > 1, m ∈ N)$ 时成立。
递推证明。根据2的假设，若能证明 $n = m + 1$ 时命题 $P$ 成立，则命题得证。

例如，有命题 $P：1+2+3...+n = n*(n+1)/2$ ，按照数学归纳法证明如下：

起始验证。当 $n$ 等于 $1$ 时， $1 = 1*(1+1)/2$ ，命题成立。
假设命题成立。假设命题等于 $m$ 时成立， $1+2+3+...+m = m*(m+1)/2$ 。
递推证明。根据2的假设，如果能证明 $n = m+1$ 时命题正确，则命题 $P$ 成立。

证明：在2所示式子左右两边加上 $m+1$ ，得到 $1+2+3+...+m+(m+1) = m*(m+1)/2 + (m+1)$

等号右边可以写成 $(m+1)*(m+2)/2$ ，显然该形式就是将 $n = m+1$ 代入原命题 $P$ 的形式，证毕。

b) 证明Dijkstra算法的正确性

命题 $P$ ：Dijkstra算法第 $n$ 次进入while时，会将第 $n$ 个顶点加入距离已确定顶点集合 $A$ 中，此时对于顶点 $∀v ∈ A($ 共 $n$ 个)，总有 $dv = δv$ 。

※ $dv$ 表示由Dijkstra算法得到的最短距离估计，对于源点 $s$ ，在程序开始时赋予 $ds = 0$ ，对于其他顶点，由松弛操作得到。 $δv$ 表示实际的顶点 $v$ 到源点的最短距离。

起始验证。当 $n$ 等于 $1$ 时， $A$ 集合中只有源点 $s$ 自身， $ds = 0$ (程序开始时赋值得到)，且知 $δv = 0$ ，故 $n=1$ 时命题正确。
假设命题成立。假设命题 $P$ 在 $n$ 等于 $m$ 时， $P(m)$ 成立，即算法经过 $m$ 次while，得到具有 $m$ 个顶点的集合 $A$ ，对于顶点 $∀v ∈ A$ (共 $m$ 个)，总有 $dv = δv$ 。
$P(m+1)$ 递推证明。根据 2 的假设，如果能证明第 $m+1$ 个顶点 $u$ 被放入集合 $A$ 时有 $du = δu$ ，则命题 $P$ 成立。

更详细地， $|A| = m$ 时，在点集 $B (B = S - A)$ 中根据算法规则找到距离最短的顶点 $u$ ，将该顶点将作为第 $m+1$ 个顶点放入A中，放入后 $|A| = m + 1$ ，如果能证明 $du = δu$ ，使得 $P(m+1)$ 成立，则对于顶点 $∀v ∈ A$ (共 $m+1$ 个)，有 $dv = δv$ 。

以反证法证明之。

3.1 🤔 假设 $m+1$ 时 $du = δu$ 不成立，即有如下式(1)，之后的目标是 根据已知条件导出某种矛盾情形，推翻该假设。

(1) $δu < du$

※ $δu$ 是实际的 $u$ 到源点的最短距离， $du = δu$ 不成立时只能是 $δu < du$ 。算法保证了从 $s$ 到 $u$ 的过程一定是一条由图中的有向边构成的 连续路径，只要是连续路径，无论有多少条这样的路径，一定有一条最短路径，其长度记作 $δu$ 。并使得其他路径长度必大于等于 $δu。$

3.2 🤔 根据3.1的假设，存在一条从源点 $s$ 到 $u$ 的路径 $Pu$ ，该路径是 $s$ 到 $u$ 的最短路径，即 $|Pu| = δu < du$ 。路径 $Pu$ 一定有不在 $A$ 集内的顶点 (至少有 $u$ 不在 $A$ 集中，注意此时 $u$ 还未被选入 $A$ 中)，同时也有在 $A$ 集中的点 (至少有 $s$ 点在 $A$ 集中)，可以假设 $Pu$ 经过 $x$ 和 $y$ ，其中 $x$ 在A中 (可以是 $s$ )， $y$ 在B中 (可以是 $u$ 本身)， $y$ 到 $u$ 的过程中也可以再进入 $A$ ，如下图。 $Px$ 为 $Pu$ 在顶点 $x$ 结束的子路径，因为路径 $Px + (x, y)$ 为路径 $Pu$ 的一部分，所以有：

(2) $|Px| + |(x, y)| ≤ |Pu| = δu$

这是显然的，因为 $Px + (x, y)$ 是 $Pu$ 的一部分，当 $y=u$ 时取到等号。

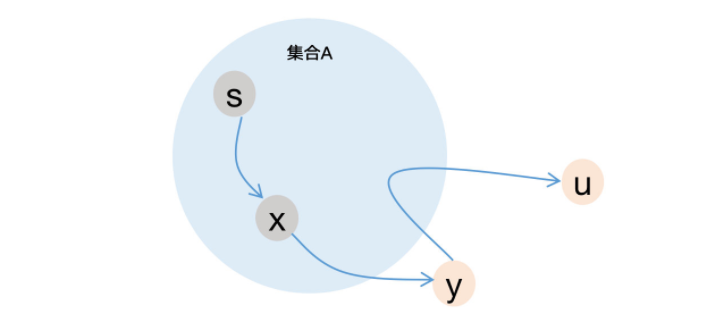
3.3 🤔 在 $x$ 之前被选中进入 $A$ 集内时，对其邻接顶点 $y$ 执行过 松弛操作，该操作会比较 $dx + |(x, y)|$ 是否小于 $dy$ ，若小于则以 $dx + |(x, y)|$ 更新 $dy$ 的值，所以如果更新了，更新之后有 $dy = dx + |(x, y)|$ ，如果没更新，说明 $dy < dx + |(x, y)|$ 。假设之后 $y$ 还会被 $y$ 的其他前驱顶点更新 $dy$ 值 (当该前驱顶点进入 $A$ 集时)，那 $dy$ 只会变得更小，所以一定有：

(3) $dy ≤ dx + |(x, y)|$

比较式 (2) 和式 (3) 中的 $|Px|$ 和 $dx$ ，因为 $dx = δx$ (由步骤2的 $P(m)$ 假设给出，顶点 $x$ 是 $P(m)$ 假设的 $m$ 个顶点之一)，而 $Px$ 只是若干从 $s$ 到 $x$ 的路径之一，因此必有 $d(x) ≤ |Px|$ ，当 $Px$ 恰是 $s$ 到 $x$ 的最短路径时取到等号。所以根据式 (2) 和式 (3) 有：

$dy ≤ dx + |(x, y)| ≤ |Px| + |(x, y)| ≤ |Pu|$ ，即

(4) $dy ≤ |Pu| = δu$

3.4 🤔 顶点 $y$ 与 $u$ 均在 $B$ 集中，根据算法规则， $u$ 作为第 $m+1$ 个定点被放入 $A$ 集中时，其在 $B$ 集中相比于 $B$ 集中的其他顶点(自然也包括 $y$ )，到源点 $s$ 的距离最小，显然有：

(5) $du ≤ dy$

结合式 (1)，式 (4)，式 (5)得到：

(6) $δu < du ≤ dy ≤ |Pu| = δu$ ，即 $δu < δu$