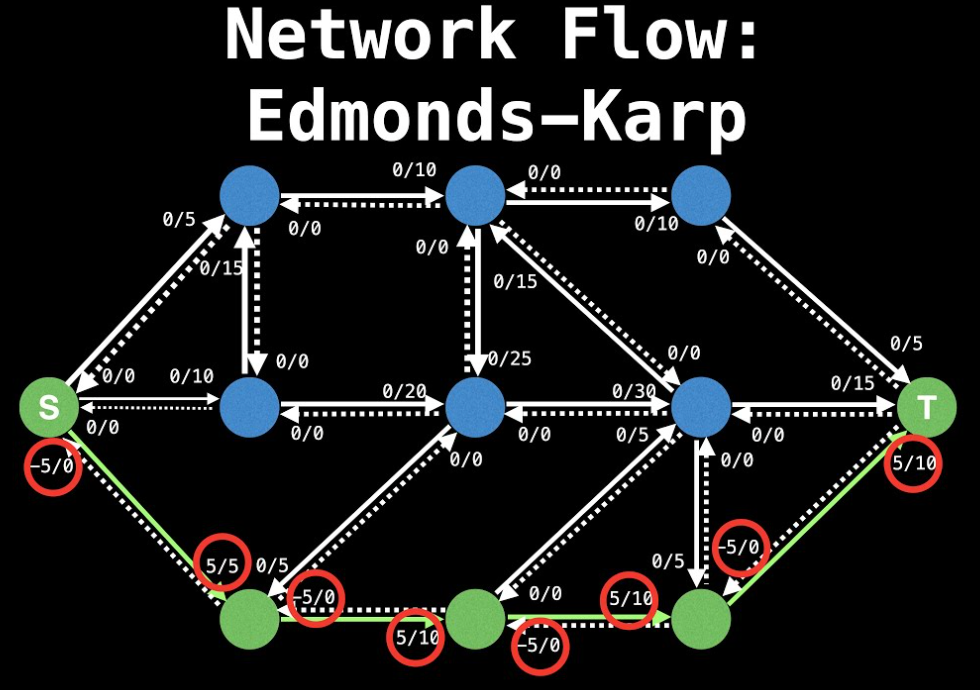
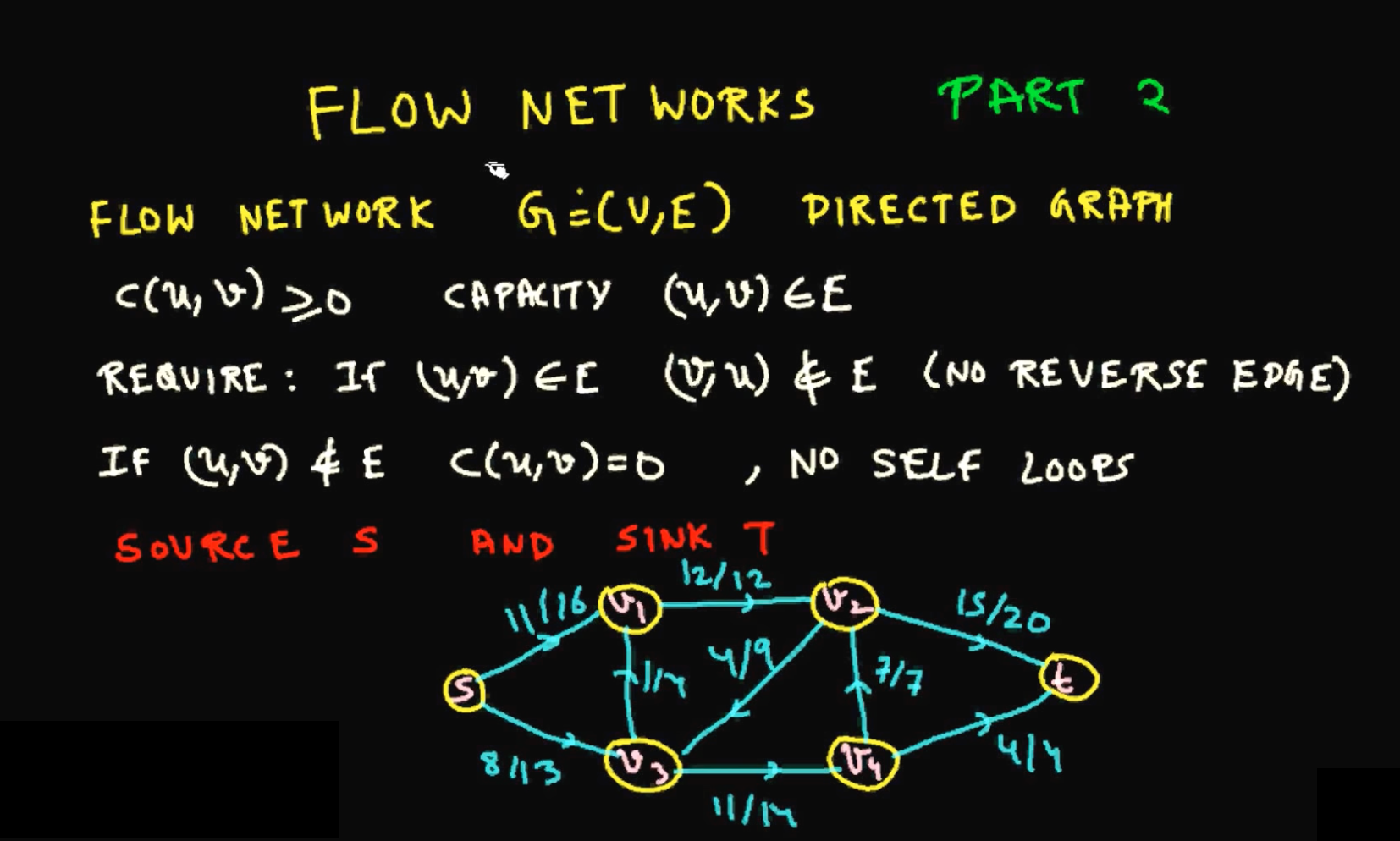
Dinic算法复杂度证明

Dinic算法复杂度证明

前段时间学习图论，对一些算法正确性和复杂度的证明有些兴趣，这篇证明是当时的一个心血之作，起初看了Dinitz老爷子本人的论文，和Cornell大学的一个lecture讲义都没看懂（其实上面都有详细证明，但我比较笨，没看懂），后来在Duke大学的lecture讲义中找到了我能看懂的证明的关键，本文的证明以其为基础。实际上Duke大学的这个证明也没完全看懂（比如他的证明里有可以取等号的地方一律取了更松的不等号，不太不明白这么做有什么好处），但它提供的思路让我最终缝合出一个(我认为)还算严谨的证明。如果你也遍寻不到令你满意的Dinic算法复杂度证明，不妨看看我的这篇文章，欢迎你的指正！

※ 本文需要先理解Edmonds-Karp算法复杂度证明。这两篇文章数月前都曾发布在知乎上。

---

Dinic算法： 相比EK算法以BFS方式实现FF方法中的增广操作，在Dinic算法中，采用BFS和DFS结合的方式增广。首先引入 高度标号(层次标号) 和 分层图 的概念。以BFS算法从 $s$ 到 $t$ ，标记 $s$ 为第1层，$s$ 的邻接顶点为第2层，以此类推 $t$ 为最后一层。执行一次BFS，赋予每个顶点高度标号信息，此时的图称作 分层图(层次图)。在此分层图内以DFS方式反复寻找增广路并执行增广操作(找到饱和边，发送和发回流)，累计发送流。完成当前分层图的所有增广操作称作 一个阶段。一个阶段结束后，重置高度标号信息，再次执行BFS得到新的分层图并重复DFS的增广操作，直到无法分层 时说明 $s$ 到 $t$ 已无增广路，算法结束，此时得到的发送流总和即为 $s$ 到 $t$ 的 最大流。

高度标号的作用：在以DFS增广时，每次从顶点 $v$ 到其邻接顶点 $w$ 的路径增长，都要考察 $w$ 的的高度是否比 $v$ 的高度大1，以此来保证路径总是能按步增长到最后一层的 $t$ (在有增广路的前提下)。

证明时间复杂度 $O(|V|^2|E|)$

如下证明参考了COMPSCI 638: Graph Algorithms, Lecture3。

1. BFS建立分层图 $O(|E|)$

可参考无权最短路径复杂度分析，略。

2. 一次DFS增广 $O(|V|)$

在分层图中，由于高度标号加一的判断条件限制，DFS只能沿着高度递增的方向从 $s$ 到 $t$ 推进，因此单次DFS推进次数最多不超过 $|V|-1$ 次，时间复杂度为 $O(|V|)$。

3. 一个阶段中DFS增广次数 $O(|E|)$

在分层图中，每次DFS增广的结果使得一条高度递增方向上的饱和边 $(u, v)$ 消失，此边的反向边 $(v, u)$ 增加。如前述，增广路只能沿着高度递增的方向，而同一阶段内(同一张分层图中)反向边是沿着高度递减方向增加的。$(u, v)$ 消失后再次出现的条件是 $(v, u)$ 为此后某次增广路上的饱和边。再次强调，在 同一阶段内 (同一张分层图中)，$(v, u)$方向是高度递减的，不可能出现在增广路上，因此一条高度递增边 $(u, v)$ 被删除后不会再次出现。一次增广至少令一条高度递增边饱和并删除，高度递增边数量不大于$|E|$，于是 一个阶段内DFS的次数最多为 $|E|$，即 $O(|E|)$。结合 2 可知，一个阶段的总复杂度为单次DFS的复杂度与DFS次数的乘积，即 $O(|V||E|)$。

4. 阶段数(分层图建立次数) $O(|V|)$

此证明是难点。 如前述，在层高递增条件的限制下，$s - t$ 最短路径长度即 $t$ 的层高，因此最短路径最大不超过 $|V| - 1$。如果能证明每次分层图使得 $s - t$ 最短路径长 「严格」递增 ，则立即推出阶段数(分层图建立次数)的上限为 $|V|$，复杂度为 $O(|V|)$。最短路径长严格递增的证明如下。

令相邻的两次分层图为 $G_f$ 和 $G_{f'}$ ，以 $d(u, v)$ 和 $d'(u, v)$ 分别表示$G_f$ 和 $G_{f'}$ 中的 $u$ 到 $v$ 的最短距离。

1. 由Edmonds-Karp算法复杂度证明已知 (这一点很重要)，删正向边加反向边的操作，使得源点 $s$ 到任意一点 $u$ 的距离是非递减的，即 必有 $d'(s, u) ≥ d(s, u)$。对证明过程稍加改造很容易得到一个对汇点 $t$ 来说类似的结论，即删正向边加反向边的操作，使得任意一点 $u$ 到汇点 $t$ 的距离是非递减的，即 必有 $d'(u, t) ≥ d(u, t)$。

   (1) $d'(s, u) ≥ d(s, u)$

   (2) $d'(u, t) ≥ d(u, t)$

对于 $s - t$ 来说有 $d'(s, t) ≥ d(s, t)$。接下来的证明目标是拿掉该不等式中的等号，证明 $G_{f'}$ 相比 $G_f$，严格地有 $d'(s, t) > d(s, t)$。可用反证法证明不可能取等号。

2. 假设 $d'(s, t) ≥ d(s, t)$ 可以取到等号。
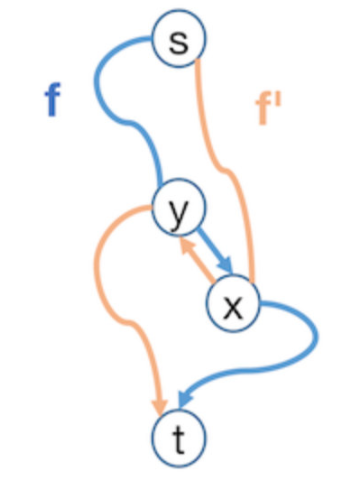
   若$G_{f'}$ 有一条 $s$ 到 $t$ 的最短路径 $f'$，则一定存在边 $(x, y) ∈ E_{f'}$，是 $G_f$ 某条增广路饱和边的反向边。因为如果 $E_{f'}$ 都是 $G_f$ 中存在的边，由于 $d'(s, t) = d(s, t)$，这样的 $f'$ 路径在 $G_f$ 中就一定已经被找到了。因此在 $G_f$ 中有 $(y, x) ∈ E_f$ ，于是有

   (3) $d(s, x) = d(s, y) + 1$

3. 由 (1) 和 (2) 易知

   (4) $d'(s, x) ≥ d(s, x)$

   (5) $d'(y, t) ≥ d(y, t)$

4. $f'$ 路径长可写成 $d'(s, t) = d'(s, x) + 1 + d'(y, t)$ ，应用 (4) 和 (5) 得到

   $d'(s, t) = d'(s, x) + 1 + d'(y, t) ≥ d(s, x) + 1 + d(y, t)$

   又由 (3) 得到

   $d'(s, t) = d'(s, x) + 1 + d'(y, t) ≥ d(s, x) + 1 + d(y, t) = d(s, y) + d(y, t) + 2$

   即

   (6) $d'(s, t) ≥ d(s, t) + 2$

由此，$d'(s, t) = d(s, t)$ 的假设不成立，但我们知道 $d'(s, t) ≥ d(s, t)$ ，因此有 $d'(s, t) > d(s, t)$ ，也即证明了Dinic算法中下一分层图的最短路径长度与前一分层图相比严格递增。

综上，总时间复杂度为每个阶段建立分层图的复杂度 $O(|E|)$ 与在该分层图内执行的总DFS复杂度 $O(|V||E|)$ 之和乘以阶段数 $O(|V|)$，为 $O((|E|+|V||E|)*|V|)$，即 $O(|V|^2|E|)$。