Edmonds-Karp算法复杂度证明

本文给出EK算法复杂度的(严格)证明，证明过程参考了这两篇文章证明1、证明2。这是我为了发布 Dinic算法复杂度证明而写的前置文章，Dinic复杂度证明用到了EK复杂度证明的一个结论。欢迎大家指正！

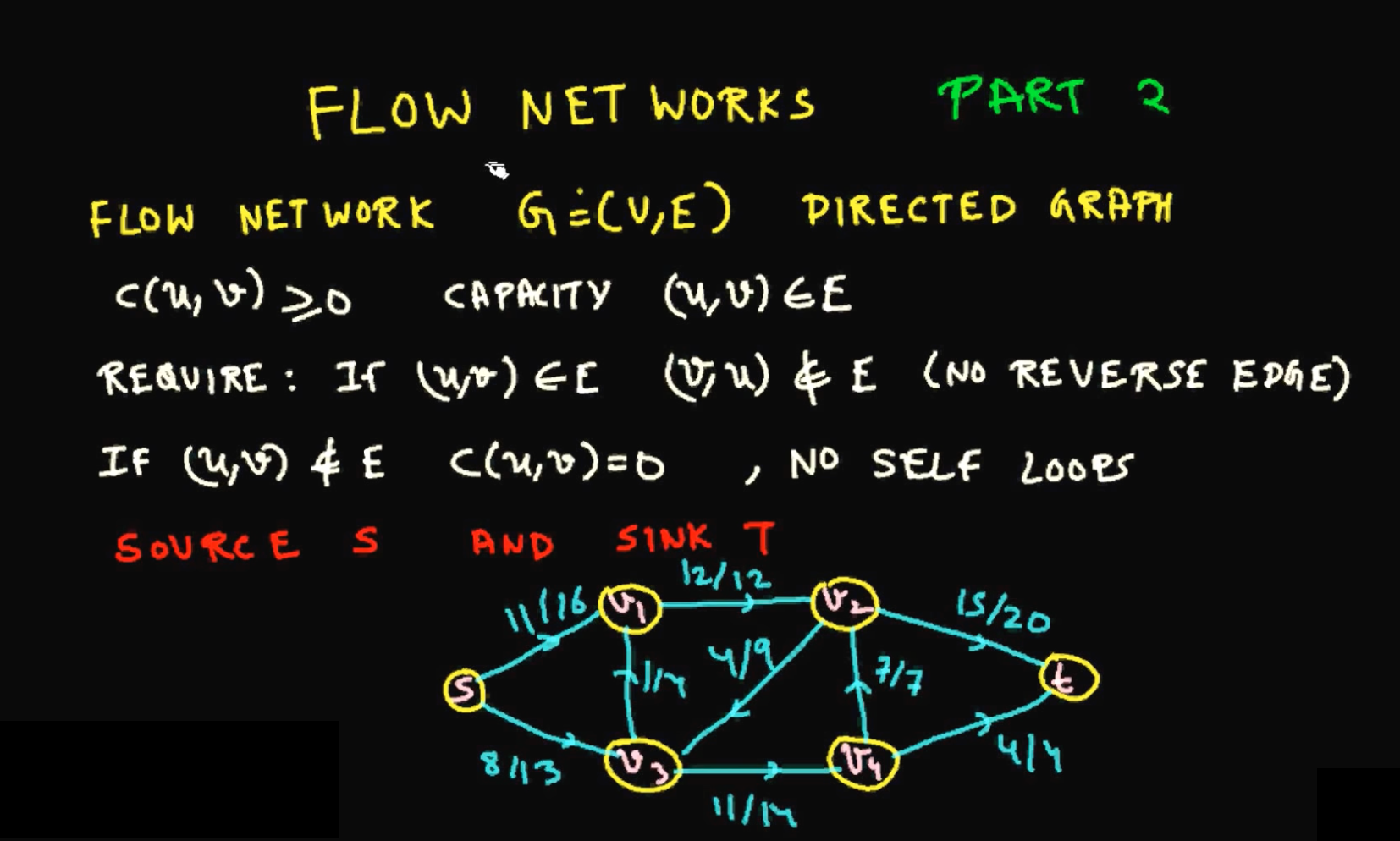
EK算法： 以BFS方式 (无权最短路径) 寻找增广路径实现 Ford-Fulkerson 方法即为 Edmonds-Karp 算法。每找到一条增广路并确定该路径上的最小边权(该路径最大可发送流)后，将此边权计入最大流中，并在此路径上对 $s > t$ 方向的边减去该权值， $t > s$ 方向上加上该权值。当BFS无法再找到增广路时算法结束，得到 $s$ 到 $t$ 的最大流。

时空复杂度

以下证明 EK 算法的时间复杂度为： $O(|V||E|^2)$

本证明参考了证明1、证明2。

1. 一次BFS增广

每次 $bfs$ 增广，在增广路上的未饱和边会多出一条反向边，原图的单向边添加反向边后，就具有双向边 (两条) ，但饱和边仍是一条 (反向) ，因此增广操作导致的边数增长不会使总边数超过原来的 2 倍，即算法的任意时刻总边数 $< 2|E|$ 。因此一次 $bfs$ 的时间复杂为 $O(2|E|)$ ，即 $O(|E|)$ 。

2. BFS增广次数

2.1 增广路长度非递减

即证明算法过程中的 $s$ 到 $t$ 的 BFS 增广操作，即正向边删除和反向边增加的操作，不会导致源点 $s$ 到任意一点 $v$ 的最短路径距离减少。残留图 $G_f$ 经过一次 BFS 增广变为 $G_{f'}$ 后，对任意顶点 $v$ ，源点 $s$ 到 $v$ 的最短路径长度 非递减，即有 $d'(s, v) ≥ d(s, v)$ 。以下利用反证法证明，并在证明中解释为何只能证明非递减而无法证明严格递增，即不是 $d'(s, v) > d(s, v)$ 。

假设某一次 $s - t$ 增广后，使得某些顶点到源点 $s$ 的最短路径距离相比增广前变小了，且这其中距离源点 $s$ 最近者为 $v$ 。则根据该假设有

(1) $d'(s, v) < d(s, v)$
令 $u$ 为 $G_{f'}$ 中 $v$ 的靠近源点 $s$ 的前一个顶点，则有

(2) $d'(s, u) + 1= d'(s, v)$

如 2.1.1 所述， $v$ 是我们有意选择的在 $G_{f'}$ 中最短距离相比在 $G_f$ 中变小的且距离 $s$ 最近的顶点， $u$ 比 $v$ 更靠近 $s$ ，但在 $G_{f'}$ 中相比在 $G_f$ 中距离 $s$ 的最短路径未变小，即有

(3) $d(s, u) ≤ d'(s, u)$
假设 $(u, v) ∈ E_f$ ，已知 $s$ 到 $v$ 的最短路径距离为 $d(s, v)$ ，则有

(4) $d(s, u) + 1 = d(s, v)$

结合(1)、(2)、(3)有

$d(s, u) ≤ d'(s, u) → d(s, u) + 1 ≤ d'(s, u)+ 1 = d'(s, v) < d(s, v)$ ，即

(5) $d(s, u) + 1 < d(s, v)$

(4) 是由 2.1.3 的假设得到的，与由 (1), (2), (3) 得到的 (5) 矛盾，故在 2.1.1 假设成立的前提下，2.1.3 的假设 $(u, v) ∈ E_f$ 不成立，即 $(u, v) ∉ E_f$ 。同时我们还能看到，如果一开始证明的是 $d'(s, v) > d(s, v)$ ，那么就要反证 $d'(s, v) ≤ d(s, v)$ (对应式(1))，经过同样的过程当前的式 (5) 会变为 $d(s, u) + 1 ≤ d(s, v)$ ，将推导不出与 (4) 式的矛盾（因为都有一个等号）。
由上述知 $(u, v) ∉ E_f$ ，但如 2.1.2 所述， $(u, v) ∈ E_{f’}$ ，故在 $G_f$ 上的增广必定经过了 $(v, u)$ ，且此边饱和，导致在 $G_{f'}$ 中产生了反向边 $(u, v)$ 。于是可知在 $G_f$ 中有

(6) $d(s, u) = d(s, v) + 1$

(6) 与 (5) 矛盾，于是最初 2.1.1 的假设不成立，即不存在这样的顶点 $v$ ，也即增广操作使得源点到任意一点 $v$ 的长度 非递减， 故EK算法寻找的增广路长度非递减。

2.2 增广次数

假设某次 $G_f$ 的增广中 $(u, v)$ 为饱和边，增广后 $(u, v) ∉ E_{f'}$ ， $(v, u) ∈ E_{f'}$ 。之后 $(u, v)$ 要再次出现的前提是 $(v, u)$ 在增广路上。在 $G_f$ 中 $(u, v)$ 第一次成为饱和边时有

(7) $d(s, v) = d(s, u) + 1$
若 $(u, v)$ 第二次成为饱和边，可知在此前的 $G_{f'}$ 中 $(v, u)$ 中在增广路上，在 $G_{f'}$ 的这次增广中有

(8) $d'(s, u) = d'(s, v) + 1$
由 2.1 的结论， $s$ 到任意顶点的最短路径非递减，即必有 $d'(s, v) ≥ d(s, v)$ ，结合 (7) 和 (8)，有

$d'(s, u) = d'(s, v) + 1 ≥ d(s, v) + 1 = d(s, u)+ 2$ ，即

(9) $d'(s, u) ≥ d(s, u) + 2$

也就是说， $(u, v)$ 第二次成为饱和边时 $s$ 到 $u$ 的最短距离至少比前一次成为饱和边时大 2。而 $s$ 到任意顶点的距离最多不超过 $|V| - 1$ ，故 $(u, v)$ 可以成为饱和边的次数最多为 $(|V| - 1) / 2$ 。每次增广至少有一条边成为饱和边，根据 2.1 中的说明，EK算法过程中边数 $< 2|E|$ ，故考虑 所有边的总的增广次数必小于 $2|E|*(|V| - 1)/2$ ，即 增广次数复杂度为 $O(|V||E|)$ 。

综上，EK 算法复杂度为 $O(|V||E|^2)$ 。

证明过程中 BFS增广使得增广路长度非递减 的结论是关键，网上有的文章声称 BFS 寻找增广路的操作使得增广路长度递增，但我们已经在 2.1.3 的叙述中指出这是不对的。根据 2.1 的证明，只能得到 非递减 的结果，但这一结论在 2.2 中足以证明任意边第二次成为饱和边时其最短路径长至少增加2，由此得到BFS次数的上界。

空间复杂度：存图空间为 $O(|V|+|E|)$ ，队列空间为 $O(|V|)$ 。总体时间复杂度为 $O(|V|+|E|)$ 。