Floyd-Warshall算法正确性证明

Floyd-Warshall

Floyd-Warshall算法(弗洛伊德算法): 求解图中任意两点的最短路径的算法。图可以是有向图或无向图，可以有负权边，但不能有负圈 (负圈上的顶点无最短路径，可无限短)。算法以 3 重循环考察任意顶点 $i$ 到任意顶点 $j$ 是否有经过任意顶点 $k$ 的可松弛路径，即对每一个顶点 $k$ (外层循环)，考察是否有 $d(i, k) + d(k, j) < d(i, j)$ ，若有则更新 $d(i, j) = d(i, k) + d(k, j)$ 。

可以这样理解其工作过程。已知确定的任意两点 $i, j$ 间有确定的最短路径 $p(i, j)$ （只要无负圈，必有最短路径）， $p(i, j)$ 由多次松弛操作得到。先假设算法是正确的 (详细证明见后述)，那么在 $p(i, j)$ 的最后一次松弛后 (通过顶点 $y$ 松弛)，得到 $p(i, j) = p(i, y) + p(y, j)$ 。同理， $p(i, y)$ 和 $p(y, j)$ 是 $p(i, j)$ 的两个部分，它们由之前的松弛操作得到。例如松弛顶点 $x$ 后得到 $p(i, y)$ ，可知 $p(i, y) = p(i, x) + p(x, y)$ ，松弛顶点 $z$ 后得到 $p(y, j)$ ，可知 $p(y, j) = p(y, z) + p(z, j)$ 。路径 $p(i, j)$ 的构建过程可以一直拆分溯源到某三个相邻顶点的连接。例如在 $p(i, j)$ 上有三个相邻顶点为 $i > a > b$ ，那么在外层循环处理 $a$ ，中层循环处理 $i$ ，内层循环处理 $b$ 时，松弛操作将 $i > a > b$ 「连接起来」（因为最短路径上的任意子路径都是最短的，必松弛）。顺着算法执行过程不难看出，算法通过外循环的 $k$ 来连接边，通过不断连接短路径产生长路径，最终增长为完整的最短路径。

算法过程

顶点间最短路径 (距离) 矩阵初始化并保存。顶点到自身距离为 0，相邻顶点间距离为边权，不相邻顶点间距离设为 $Infinity$ 。若要求输出路径本身，则需要另一个最短路径信息矩阵。
以 3 个循环 (循环操作对象是所有顶点) 考察 $i$ 到 $j$ 是否可经由 $k$ 松弛。 $k, i, j$ 分别对应外，中，内层循环。
松弛操作。若 d(i, k) + d(k, j) < d(i, j) ，则 d(i, j) = d(i, k) + d(k, j) ，若有路径信息矩阵，对应更新。

递归输出路径：通过路径信息的矩阵。 $d[i] [j]$ 的值是 $k$ ，即 $i$ 经过 $k$ 到 $j$ ，在每次松弛时更新 $k$ 。例如有最短路径 $i > a > b > c > j$ 。程序结束后得到的路径信息矩阵如下。

顶点	$i$	$a$	$b$	$c$	$j$
$i$	$null$	$null$	$a$	$null$	$b$
$a$	$null$	$null$	$null$	$null$	$null$
$b$	$null$	$null$	$null$	$null$	$c$
$c$	$null$	$null$	$null$	$null$	$null$
$j$	$null$	$null$	$null$	$null$	$null$

利用该矩阵，通过递归即可找到 $i > a > b > c > j$ 。递归过程大致如下，顶点输出顺序即为路径顺序。

i > j, 找到b
  i > b，找到a
    i > a为null，输出i
    a > b为null，输出a
  b > j，找到c
    b > c为null，输出b
    c > j为null，输出c
 最后输出j

正确性证明(说明)

该算法的 本质是动态规划 ，以状态转移方程的形式描述如下，其中 $dp[k][i][j]$ 表示 经过前 $k$ 个顶点的松弛，得到的顶点 $i$ 到顶点 $j$ 的最短路径长度 。注意第一维的 $k$ 表示 $k$ 个顶点，第二维和第三维表示具体的顶点。

1
2
3

1. 定义: dp[k][i][j] 表示经过前 k 个顶点的松弛，得到的顶点 i 到顶点 j 的最短路径长度。
2. 边界: dp[0][i][j] = Infinity
3. 递推: dp[k][i][j]  = min{dp[k-1][i][j], dp[k-1][i][k]  + dp[k-1][k][j]}

最短路径 不经过 第 $k$ 个顶点 (顶点 $k$ ): $dp[k][i][j] = dp[k-1][i][j]$

最短路径经过第 $k$ 个顶点 (顶点 $k$ ): $dp[k][i][j] = dp[k-1][i][k] + dp[k-1][k][j]$

// floyd核心伪代码
for(k : V)
  for(i : V)
    for(j : V)
      if(d(i, k) + d(k, j) < d(i, j))
        d(i, j) = d(i, k) + d(k, j)

补充说明：已知点 $i, j$ 之间的最短路径为 $p(i, j)$ ，那么 $p(i, j)$ 上的任意两点 $a, c$ 的最短路径确定在 $p(i, j)$ 上。反证法简单可证。假设 $p(i, j)$ 上两点 $a, c$ 之间的最短路径经过一不在 $p(i, j)$ 上的顶点 $b$ ，那 $i, j$ 的最短路径也就不是 $p(i, j)$ ，而是 $p(i, a) + p(a, b) + p(b, c)+ p(c, j)$ 。

实例分析

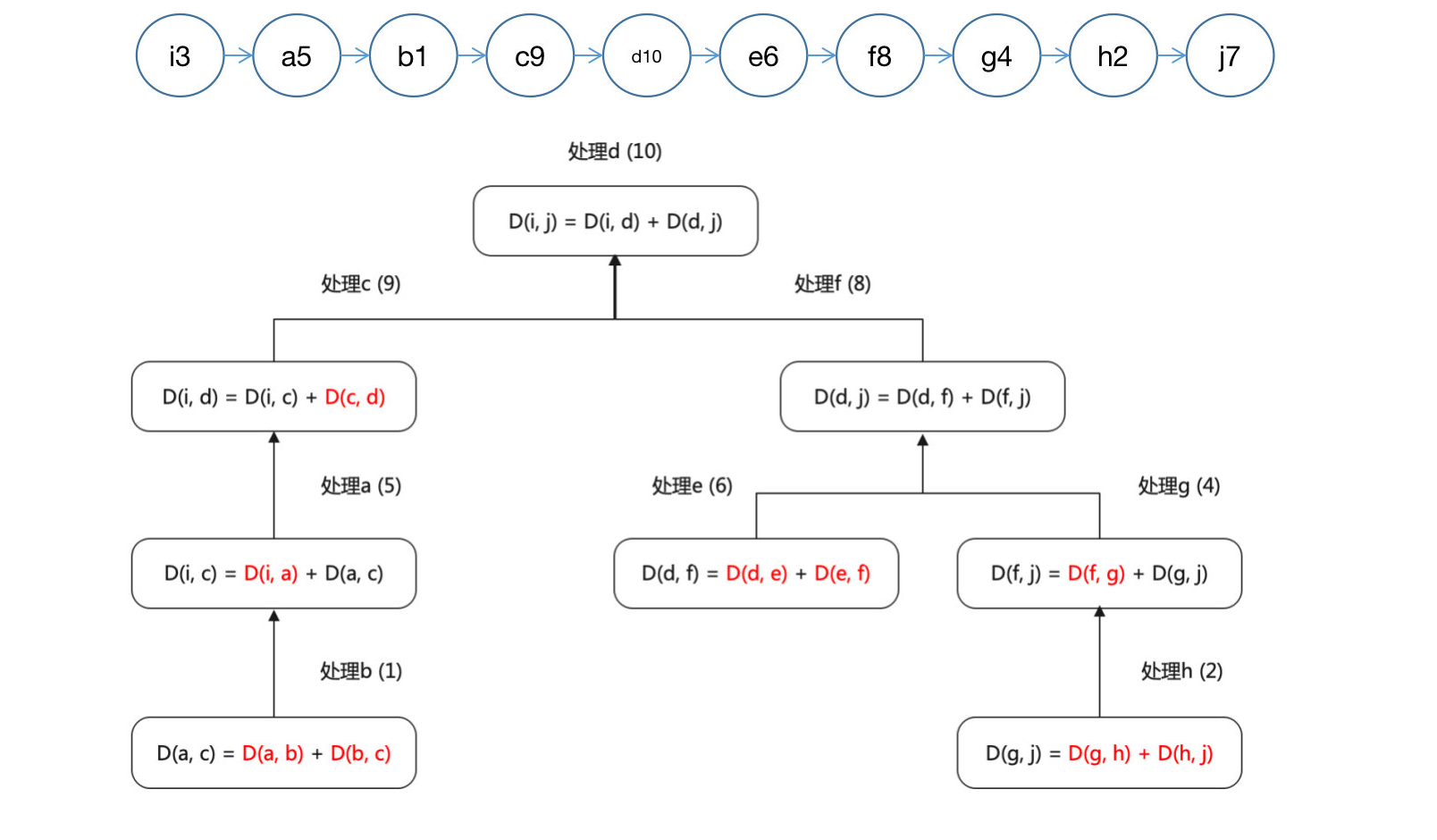
下面通过一个例子观察 Floyd 算法的动态规划过程，对其正确性可以有更直观的感受。由于算法总是在整张图上进行处理，展示整张图将使过程变得杂乱，因此我们只选取一条 $i$ 到 $j$ 的最短路径，展现该路径的构建过程。由于这条路径是随意选取的，其他所有在图上的 任意两点 的路径的构成都是类似的。

设图 $G$ 中 $i, j$ 间最短路径 $p$ 为 $i > a > b > c > d > e > f > g > h > j$ 。最外层循环对该路径上顶点的处理顺序可以是任意顺序，例如 $b, h, i, g, a, e, j, f, c, d$ (分别标上序号 1, 2, 3, 4, 5, 6, 7, 8, 9, 10，表示外层循环处理的先后顺序)。现在我们以溯源的方式从处理最后一个顶点 $d$ 得到 $d(i, j)$ 开始观察，且只观察程序对上述十个顶点的处理（对其他顶点的处理形成其他路径）。该路径的取得只与三个循环对该路径上的顶点的操作有关，循环对其他顶点的操作不影响结果，因为其他顶点不在该最短路径上，由它们导致的松弛不影响路径 $p$ ，或者说 $p$ 会从若干条 $i$ 到 $j$ 的路径中胜出。

外层循环处理 $d$ 之后由 $d(i, d) + d(d, j)$ 的结果得到 $i$ 到 $j$ 的最短路径长 $d(i, j)$ ，因此 $d(i, d)$ 和 $d(d, j)$ 此时必是已知的。继续溯源，看看 $d(i, d)$ 和 $d(d, j)$ 是如何得到的。到 $d$ 的路径上 $c$ 是最后被处理的，处理 $c$ 时计算 $d(i, d) = d(i, c) + d(c, d)$ ，其中 $d(c, d)$ 是边长，这是程序开始时已知， $d(i, c)$ 需要继续溯源， $d(i, c) = d(i, a) + d(a, c)$ ，其中 $d(i, a)$ 是边长， $d(a, c) = d(a, b) + d(b, c)$ ， $d(a, b)$ 和 $d(b, c)$ 是边长。其余过程如图，标红处表示相邻的顶点的边长，在程序开始时得到。

可以看出，外层循环处理 i 到 j 的最短路径的所有顶点的过程中，先处理的顶点得到 子路径总能够为后处理的顶点构建更长的子路径 ，直到处理 (最短路径上的) 最后一个顶点时，将两个子路径连接起来形成最终的最短路径，这正是动态规划过程的体现。

不同于 BF 动态规划过程的单串单依赖，Floyd 动态规划是 多依赖 的。也可以描述为某一次的松弛形成的路径 不一定直接作用于下一次松弛 ，而是在之后某一次松弛中发生作用。例如处理 $b(1)$ 和处理 $h(2)$ 是外层循环的两次相邻的操作，它们分别产生了两条不相连的子路径 $a>b>c$ 和 $g>h>j$ 。之后外层循环处理 $a(5)$ 时 $a>b>c$ 增长为 $i>a>b>c$ ，处理 $c(9)$ 时增长为 $i>a>b>c>d$ 。 $g>h>j$ 在外层循环处理 $g(4)$ 时增长为 $f>g>h>j$ ，处理 $f(8)$ 时增长为 $d>e>f>g>h>j$ ( $d>e>f$ 在外层循环处理 $e(6)$ 时得到)。最终在处理 $d(10)$ 时得到 $i > a > b > c > d > e > f > g > h > j$ 。

总结 Floyd 算法的过程，外层循环执行完第 $k$ 次，给出由 $k+1$ 条边组成的路径，下一次会利用长度为 $1, 2, ... , k+1$ 的路径连接出长度为 $k+2$ 的路径。这就好像将任意两点连成单边线（只要这两点之间存在路径），然后再将两条单边线作为零件连成长度为 2 的线，因为具备所有单边线，所以无论长度为 2 的线是由哪些单边线组成的，都可以找到并连起来。然后再利用长度为 1，2 的线作为零件连成长度为 3 的线，因为无论一条长度为 3 的线是如何构成的，构成它的单边线和 2边线都已具备。以此类推直到连出所有可能长度的线。