最大流最小割定理证明

最大流最小割定理

最大流最小割定理(Max-flow min-cut theorem)：对于一张网络图 $G$ ，从源点 $s$ 到汇点 $t$ 的 最大流量等于最小割所有割边容量之和。

以下将从 路径存在问题 引入 割和割的大小 的概念，再由割的大小与 $s-t$ 不相交路径数量的关系，证明该定理。证明过程中先假设有向图 (网络) 边无权 (或者说均为单位边权，即边权为1)，随后再推广至有权图。

证明内容整理自B站南大老师蒋炎岩的授课视频: [算法竞赛入门] 网络流基础: 理解最大流/最小割定理。

在这里我们提前指出 Ford-Fulkerson 方法的正确性证明与最大流最小割定理的证明等价 ，这意味着它们会被 同时证明 。如下，也就是 $k = m$ 与 $k = l$ 同时成立，后续我们将理解这一点。

Ford-Fulkerson方法的正确性证明：图 $G$ 中 $s-t$ 的最大流为 $k$ ，FF 方法找到的流量为 $m$ ，证明 $k=m$ 。
最大流最小割定理证明：图 $G$ 中 $s-t$ 的最大流为 $k$ ， $s-t$ 最小割大小为 $l$ ，证明 $k=l$ 。

L. R. Ford Jr. & D. R. Fulkerson (1962) Flows in Networks, 这一论文第23页，作者给出的最大流最小割定理描述如下。

Theorem 5.1 Max flow min cut theorem.

For any network the maximal flow value from $s$ to $t$ is equal to the minimal cut capacity over cuts separating $s$ and $t$ .

从路径存在问题到割

$s-t$ 流 (flow) 存在的前提是 $s-t$ 路径存在。对于路径存在问题，通常以 $DFS/BFS$ 算法判定，算法从 $s$ 出发找到 $t$ 则说明 $s-t$ 路径存在，否则不存在。为了引入割的概念，现在尝试以更本质的方式考察该问题。首先以排列组合的方式简单罗列所有可能的 $s-t$ 路径。例如一张包含顶点 $s, a, b ,c, d, t$ 的图，可以罗列出如下路径，暂不考虑边是否存在。

s > t
s > a > t
s > b > t
...
s > a > b > t
s > a > c > t
...

对于上述列表中的一条路径，若该路径中的每对相邻顶点构成的边均存在，则该路径为一条 $s-t$ 路径。若对于列表中的所有路径都能找到不存在的边，则证明该图不存在 $s-t$ 的路径。

对于路径存在问题，罗列所有可能路径并逐一判断的方法虽最严格，但显然不是证明的好办法。再次考虑 $DFS/BFS$ ，算法从 $s$ 出发，会找到所有能到达的顶点，将这些顶点作为集合 $S$ ，剩下 $s$ 无法到达的顶点作为集合 $T$ 。 $s-t$ 路径不存在， 等价于 $S$ 中任意顶点到 $T$ 中任意顶点的连边都不存在 ，由此引入如下割的概念。

割的定义：割 (cut) 是图 $G$ 的 顶点集 $V$ 的划分 。有向图 $G(V, E)$ 的 $s-t$ 割 $C = (S, T)$ 指 $V$ 被划分为顶点集 $S$ 和 $T$ ，且 $s ∈ S$ ， $t ∈ T$ 。

割的大小：对于上述割，其大小指从 $S$ 到 $T$ 的边的数量，即边 $(u, v) ∈ E | u ∈ S, v ∈ T$ 的数量，称这些边为割边。

根据割及其大小的定义，只要存在 $s-t$ 路径，无论如何划分 $V$ 得到 $s-t$ 割，总能在图中找到从 $S$ 到 $T$ 的边，即该割的大小一定大于0。例如下面的 $s-t$ 路径， $s, a, d, e, h ∈ S， b, c, f, g, i, t ∈ T$ ，红箭头表示 $s-t$ 割的边。只要满足 $s ∈ S$ ( $s$ 在绿色阴影里)， $t ∈ T$ ( $t$ 不在绿色阴影里)，在有路径的情况下，红箭头一定存在，而与绿色阴影的形状 (具体的 $s-t$ 割) 无关。反过来说就是 若 $s-t$ 路径存在，则所有 $s-t$ 割的大小都大于0 。

因此，要想证明 $s-t$ 路径不存在，只需要找到一个大小为 0 的 $s-t$ 割即可 。注意，当 $s-t$ 路径不存在时，也可能存在大小不为 0 的 $s-t$ 割，很容易找到相关例子，因此重申，证明 $s-t$ 路径不存在是要找到一个大小为 0 的 $s-t$ 割。

不相交路径数量与割的大小

现在，我们初步建立了「流」与「割」在特定情形下的联系，即上述分析给出的「 $s-t$ 路径数量为 0 时 (流为0)，必存在大小为 0 的 $s-t$ 割」。这是「 $s-t$ 路径数量」与「 $s-t$ 割大小」的特定关系。再次回到定理内容，定理描述了「最大流」和「最小割边容量」(对无权图来说即割边数量) 的关系，不难理解，最大流就是 不相交的 $s-t$ 的路径 数量 (再次注意，我们当前讨论的是无权图，「数量」即「流量」)。 $s-t$ 的 不相交 路径指对于多条 $s-t$ 路径，它们之间 没有公共边 。后续我们通过如下三个量的关系来证明定理，即证明 $k = l$ 。

$k$ 为图中 实际存在的 $s-t$ 不相交路径数量。
$m$ 为 算法找到的 $s-t$ 不相交路径数量。
$l$ 为图中最小 $s-t$ 割边数量。

不相交路径数上界

假设图有 $k$ 条 $s-t$ 的不相交路径，想要知道 $k$ 的大小，可以逐步假设 $k (k = 0, k = 1, k = 2,...)$ ，再验证是否确实有那么多条。例如假设 $k=0$ 时，实际上就是前述 $s-t$ 路径存在性问题，已经指出，若存在大小为 0 的 $s-t$ 割，则 $k=0$ 。当 $k > 0$ 时，考虑是否还能用 $s-t$ 割的大小表达不相交路径数量。

下图 $k=1$ ，以图中的阴影表示 $s-t$ 割，可以看出该割的大小为 1。容易看出 不相交路径数量受到割边 $(b, c)$ 数量的限制 ，如果所有 $s-t$ 割大小最小为1，那么任意 $s-t$ 路径一定都经过该唯一割边，即 $s-t$ 不相交 路径至多为 1。若最小割大小为 2，则存在 2 条经过 2 条不同割边的 $s-t$ 路径。总之， $s-t$ 割的大小 $c$ 决定了 $s-t$ 不相交路径数量 $k$ 的上界，即 $k ≤ c$ 。如果 $c = l$ ，自然就有 $k≤l$ ，任意 $s-t$ 割的大小 $c$ 是 $k$ 的一个上界， $l$ 是 $k$ 的 最紧上界 。现在我们离目标近了一步，即「割边数」 $c$ 和「最大流」( $s-t$ 不相交路径数量) $k$ 的关系满足: $k ≤ c$ ，最紧地有 $k≤l$ 。

不相交路径数下界

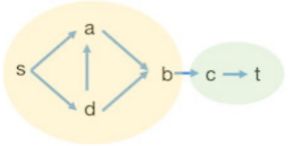
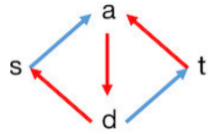
上述以割边数给出了不相交路径数量 $k$ 的上界，而如果能直接找到 $m$ 条不相交路径，此 $m$ 可立即作为 $k$ 的一个下界，且若 $m = l$ ，便可得到 $k = l$ 。直接地，我们用 $DFS/BFS$ 求 $m$ ，在 $G$ 中寻找一条 $s-t$ 路径 $p$ ，找不到时 $k=0$ ，若能找到，为了保证找到的路径总是 不相交 的，需要从 $G$ 中删去 $p$ ，然后 $k = k + 1$ 。看起来有效，但实际操作后我们会发现一个问题，如下图，当第一次选择的路径为 $s > d > a > t$ 后，由于该路径被删除，将无法再找到下一条路径，而该图显然有 $k=2$ ( $s > a > t, s > d > t$ )，因此单纯使用 $DFS/BFS$ 算法得到的 $m$ 并不一定是 $k$ 。而 Ford-Fulkerson 方法可以解决这一问题，即 FF 方法保证 $m = k$ 。

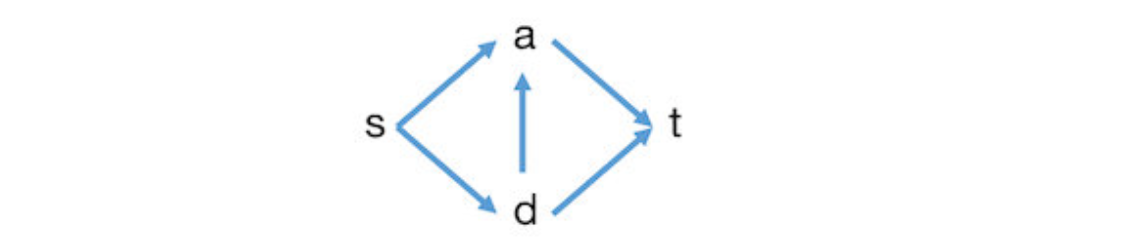
反向边 (路径)

L. R. Ford, JR & D. R. Fulkerson 在1956年的论文中修正了单纯以 $DFS/BFS$ 找最大流的缺陷缺陷，并证明了改进后算法的正确性，这就是著名的 Ford-Fulkerson 方法。修正办法十分简单，即在每一次找到一条路径并删除该路径后，在 $t-s$ 的方向上 ( $s-t$ 的反方向) 添加原路径的反向路径，仅此而已。如前图，找到 $s > d > a > t$ 的路径后将其删除，立即添加 $t > a > d > s$ 路径。该操作使得后续仍能找到一条 $s-t$ 路径，即 $s > a > d > t$ ，继续删除并添加相应的反向路径，最终无法再找到 $s-t$ 路径， $m=2$ 被正确求出。

$s-t$ 路径称为 增广路径(Augmenting Path)，可以将反向路径称作 反向增广路径。添加这一反向路径的操作是整个算法最为核心的部分，以下证明这一操作的正确性，即以「寻找增广路-删除该路径-添加反向路径」这一FF方法得到 $m$ 条 $s-t$ 路径，且 $m = k$ 。稍等，我们不是要证明「最大流最小割定理」，也就是证明 $k = l$ 吗？为何突然转为证明 $m=k$ ？很快你会看到，这两点是等价的，且是同时证明的。

证明k=m

蒋岩炎老师的视频中不以严谨的数学证明，而是以图形化的直观方式证明了最大流最小割定理 (也即证明了 FF 方法的正确性)。

添加反向边的有效性

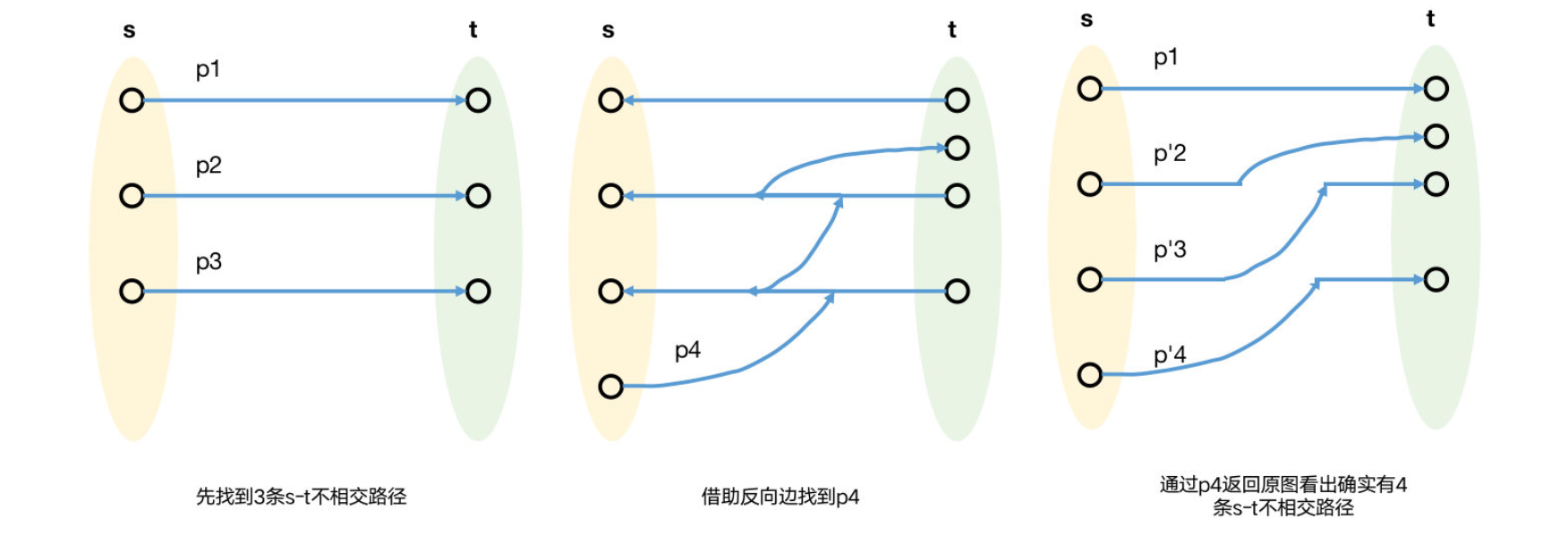
如下左图 (图中的 $s$ 和 $t$ 虽画出了多个点，但表示一个点)， $p1, p2, p3$ 是 $DFS/BFS$ 找到的头 3 条 $s-t$ 不相交路径 (每次都会添加反向路径，但这三条恰好都还未经过反向边)， $p4$ 是第 4 条 (经过反向边)。 $p4$ 由两种边组成，如下中图，一种是不与 $p1, p2, p3$ 交叠的边，即此前尚未出现在不相交路径上的原边，另一种是与 $p2$ 和 $p3$ (反向) 交叠的边，这些边是找到 $p2$ ， $p3$ 后添加的 反向边，它们使得 $p4$ 可以沿着这样的反向边到达 $t$ 。假设此时 FF 方法已找不到 $s-t$ 路径，那么 FF 方法找到了 4 条不相交路径，即 $m = 4$ 。

$p4$ 是通过添加反向边来间接得到的 (此路径并不存在于原图中)，现在的问题，由于 4 条路径是通过添加反向边找到的，它们并不都是原图中存在的路径。我们首先明确原图中确实有 4 条不相交路径。为了看出这一点，找到 $p4$ 后，在反向 $p4$ 之前，去掉 $p4$ 走过的反向边，然后将还原 $p1, p2, p3$ 反向过后的边 (再反回去) ，得到下右图。可以看到， $p1$ 不变，而 $p'2, p'3, p'4$ 就是原图中的 $s-t$ 路径，它们显然不相交。注意下右图本身就是原图的一部分，只不过一开始没找到 $p'2, p'3, p'4$ ，而是找到了 $p2, p3$ ，然后通过反向边找到了 $p4$ 。

尽管算法找到的路径与下右图显示的原图上的路径不同，但数量是正确的。如果还有 $p5$ ，仍然可以通过相同的方法证明原图中有 5 条不相交路径。在示意图中那些通过反向边得到的 (在原图中不存在的) 路径看起来就像是切开了起初得到的路径 ( $p2, p3$ )，并通过部分原边连接这些路径的断点，使得 $s$ 到 $t$ 可达。

k的确定与最小割的大小

上述内容说明了添加反向边能够找到新的 (在不添加反向边时可能找不到的) 不相交路径，并且我们看到算法找到的路径与原图实际的路径 一一对应 (数量相等) 。有了这些准备工作，我们开始证明 $k = m$ 。证明基于以下思路。

已经知道 $m = 4$ ，因此 $k ≥ m = 4$ 。
如果找到原图 $G$ 的 $s-t$ 割 $C$ ，证明它是「最小割」且 $l = 4$ ，那么证明就完成了。
对于 2，指出一个割，直接证明它是 「最小的」 是困难的，因此我们不必考虑它是不是最小，转而考虑在原图中寻找一个大小 $c=4$ 的割 $C$ 。因为 $m≤k≤c$ ，那么 $m=k=c=4$ ，确定了 $k=4$ ，就不可能存在大小小于 4 的割，于是 $m=k=l=c=4$ 。
上述 3 就意味着 FF 方法 ( $m=k$ ) 和最大流最小割定理 ( $k=l$ ) 同时得证。

根据这个思路，我们接着前图继续分析。再次强调，现在的目标是 在原图中寻找一个大小为 $c=4$ 的割 $C$ 。

以上中图为例，将 $p4$ 反向得到如下残留图 $G_{f'}$ 。

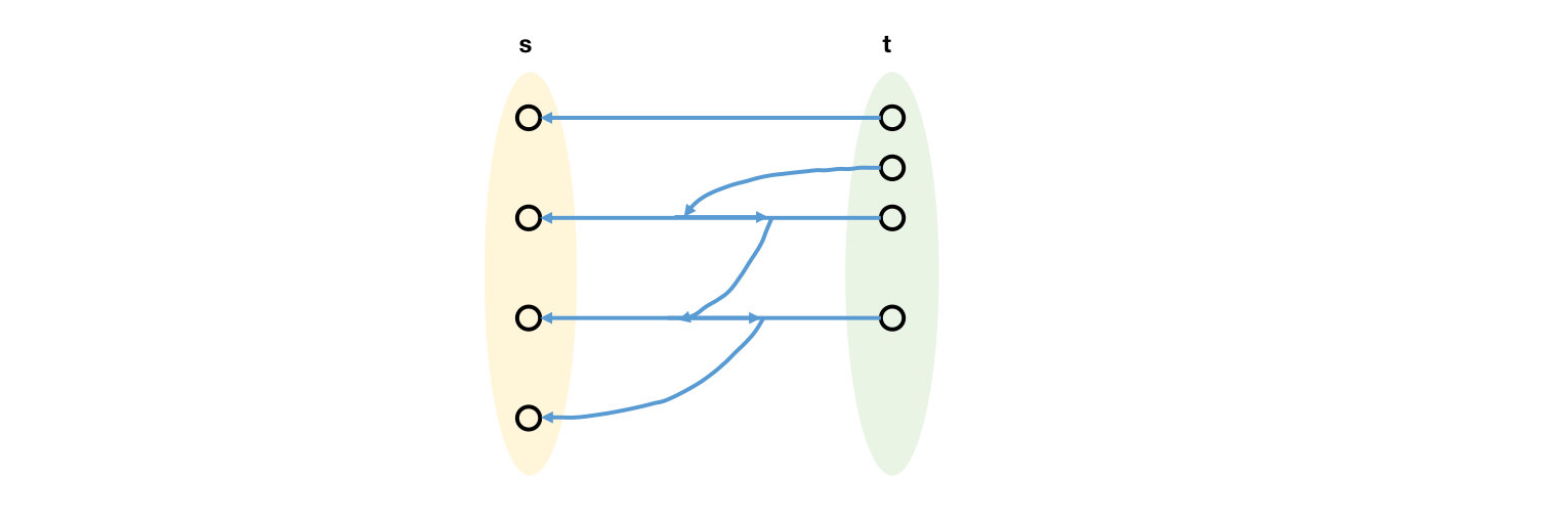
残留图 $G_{f'}$ 有两种边 ，一种是 $s-t$ 不相交路径的反向边（注意，这里说的 $s-t$ 不相交路径不是通过算法找到的路径，而是前述说明中 $p1, p'2, p'3, p'4$ 那样的原图中存在的 $s-t$ 路径），一种是其他不在不相交路径上的原边。显然，此时 $t-s$ 不相交路径就是原图上的 4 条 $s-t$ 不相交路径的反向路径。由于 $s-t$ 已不连通，可知此时在残留图中存在大小为 0 的 $s-t$ 割 $C$ 。我们指出如下具体的割 $C$ 。

割 $C$ : 将 $G_{f'}$ 中 $s$ 能够到达的顶点划归 $S$ ，将剩下的顶点划归 $T$ 。

该割大小为 0 ，反证法简单可证明。若有割边，也就是还能从 $S$ 找到一个顶点 $v$ 连到 $T$ 中的某个顶点 $u$ ，那么 $s$ 就能通过 $v$ 连通 $u$ ，这与我们的划分要求相矛盾，因为在 $G_{f'}$ 中已经将 $s$ 能到达的所有顶点都划入 $S$ 了。 $u$ 也不可能是 $t$ ，因为 $G_{f'}$ 中 $s-t$ 不连通，因此假设不成立，此割无割边。由此得到如下重要推论。

推论: 割 $C$ 在原图 $G$ 中大小为 4。

证明如下:

割 $C$ 在残留图 $G_{f'}$ 中大小为 0 ，也就是 $S$ 中无顶点可到 $T$ 。
残留图与原图的区别仅仅是 不相交路径的方向相反 。
在原图 $G$ $G$ 中， $S$ $S$ 中的顶点可分为不在 $s-t$ $s - t$ 路径上和在 $s-t$ $s - t$ 路径上的顶点。对于前者，根据 1，无顶点可到 $T$ $T$ ，对于后者，它们 贡献且仅贡献了 4 条割边 。
1. 也就是说每条 $s-t$ 路径只贡献一条割边，这要求每条 $s-t$ 路径都只穿过一次 $S-T$ 。
2. 因为原图 $G$ 的 $s-t$ 路径是残留图 $G_{f'}$ 的 $t-s$ 路径的反向路径。因此证明原图中 $s-t$ 路径只穿过一次 $S-T$ 等价于证明残留图中 $t-s$ 路径只穿过一次 $T-S$ 。(记住，割 $C$ 在原图和残留图中是一样的)
3. 假设在残留图 $G_{f'}$ 中 $t-s$ 路径穿过了两次 $T-S$ ，因为 路径是连续的 ，穿越过程必然是 $T→S→T→S$ ，也就是会有边穿越 $S-T$ 。这与残留图 $G_{f'}$ 存在大小为 0 的 $s-t$ 割相矛盾 ( $G_{f'}$ 上的割 $C$ )。
4. 因此原图 $G$ 中的 $s-t$ 路径均只穿过一次 $S-T$ ，每条路径只贡献一条割边，也即割 $C$ 在原图 $G$ 中大小为 4 。

推论得证。

至此，通过找到残留图 $G_{f'}$ 上大小为 0 的割 $C$ ，我们证明了割 $C$ 在原图中大小为 4 ，实现了证明目标。最后总结如下。

我们在指出原图 $G_f$ 上的割 $C$ 时，并不知道它是不是最小割，但证明了 $m = c = 4$ ，而我们知道 $m≤k≤c$ ，因此直接得到了 $k = m = 4$ 。因为 $k=4$ ，所以原图上的任何 $s-t$ 割不可能比割 $C$ 更小，于是 割 $C$ 是一个最小割 ，综上，有 $m=k=l=c=4$ 。
$m=k$ 证明了 Ford-Fulkerson 方法的正确性， $k = l$ 证明了最大流最小割定理，这就是我们在开始证明时提到「FF 方法正确性和最大流最小割定理的证明等价，它们会被同时证明」的原因。