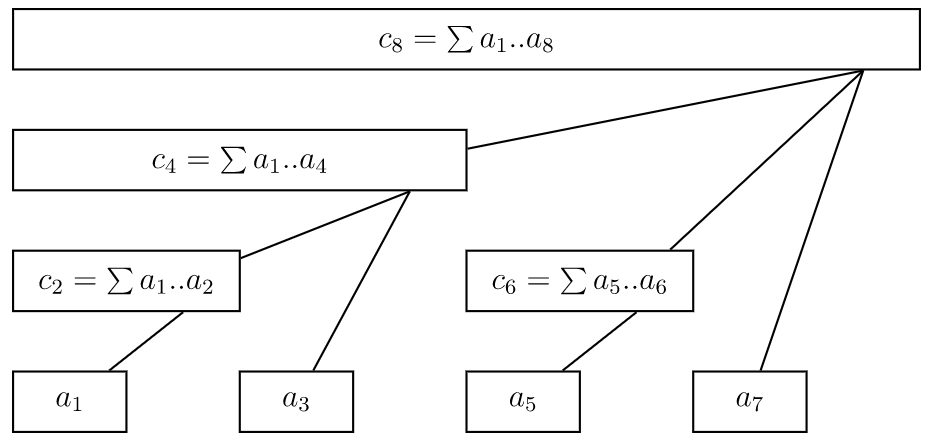
树状数组从入门到下车
树状数组是一种能够高效求解「区间问题」的数据结构。「区间问题」指的是对于大小为 n 的输入数组 nums ,通过其上执行「区间求和」、「区间修改」等操作 (通过不同类型的树状数组) 来处理的问题,解决区间问题的过程中通常还伴随着针对单个元素的「单点查询」、「单点修改」这两种单点操作。
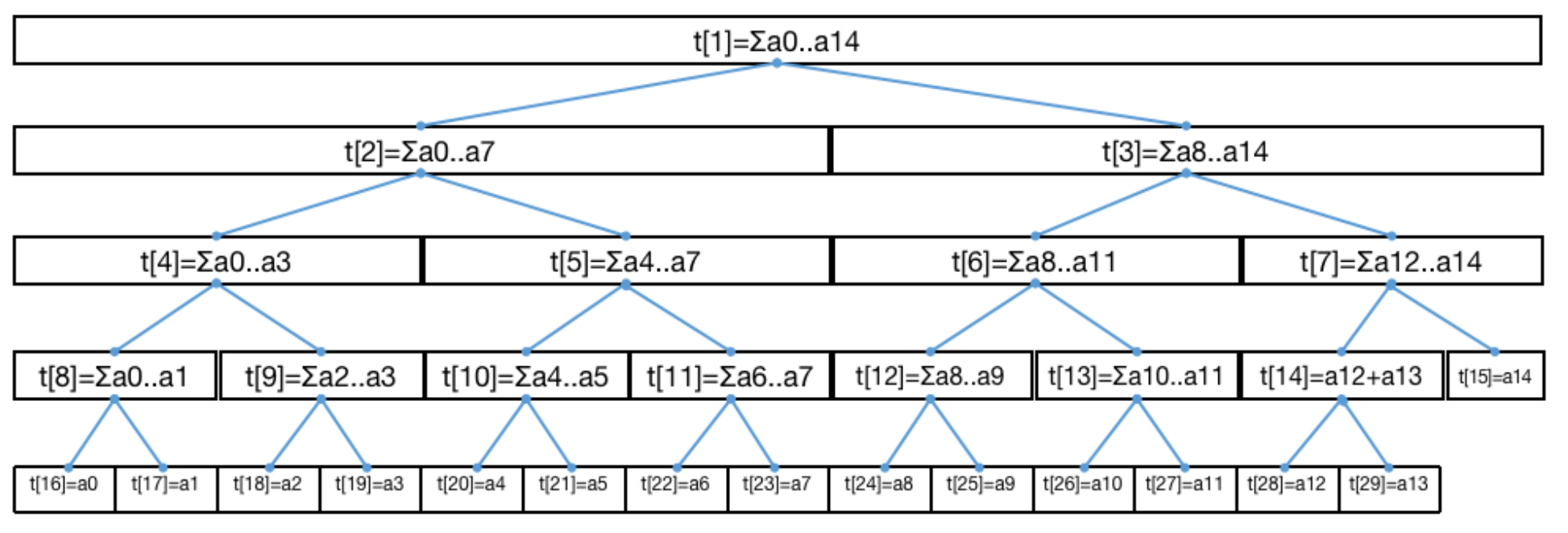
线段树从入门到急停
线段树是著名的用于高效求解「区间问题」的数据结构。「区间问题」即对于输入数组 nums ,在其上执行「区间求和」 、「区间修改」等操作,通常还伴随着针对单个元素的「单点查询」、「单点修改」这两种单点操作。
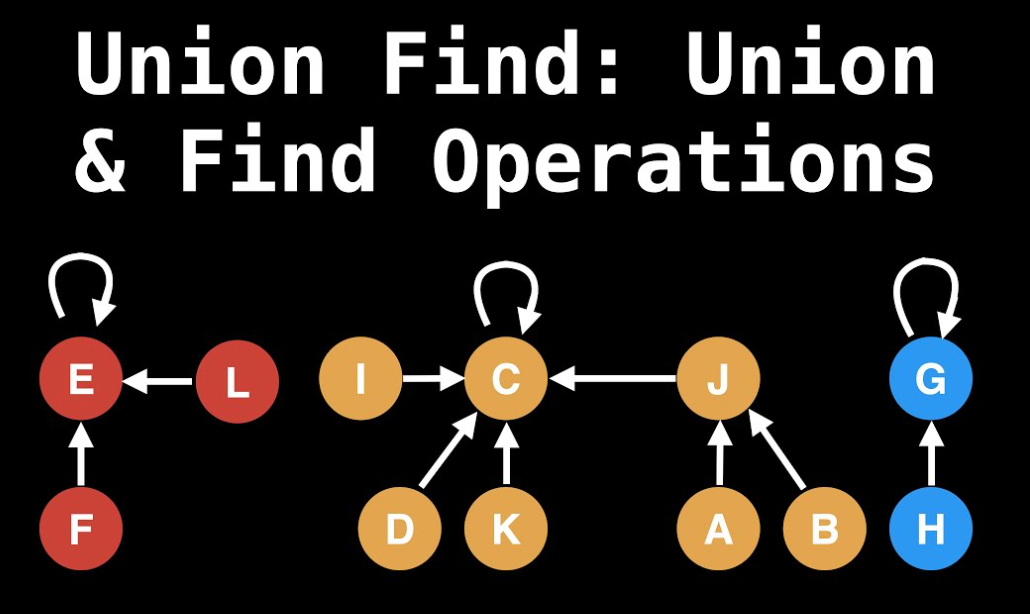
并查集从入门到出门
并查集 (不相交集) 是一种描述不相交集合的数据结构,即若一个问题涉及多个元素,它们可划归到不同集合,同属一个集合内的元素等价(即可用任意一个元素作为代表,比如上述的互为亲戚即互相等价),不同集合内的元素不等价。本文将带领读者重新发明并查集。
十大排序从入门到入赘
两万五千字全面介绍如下十种排序算法:冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、基数排序、桶排序。
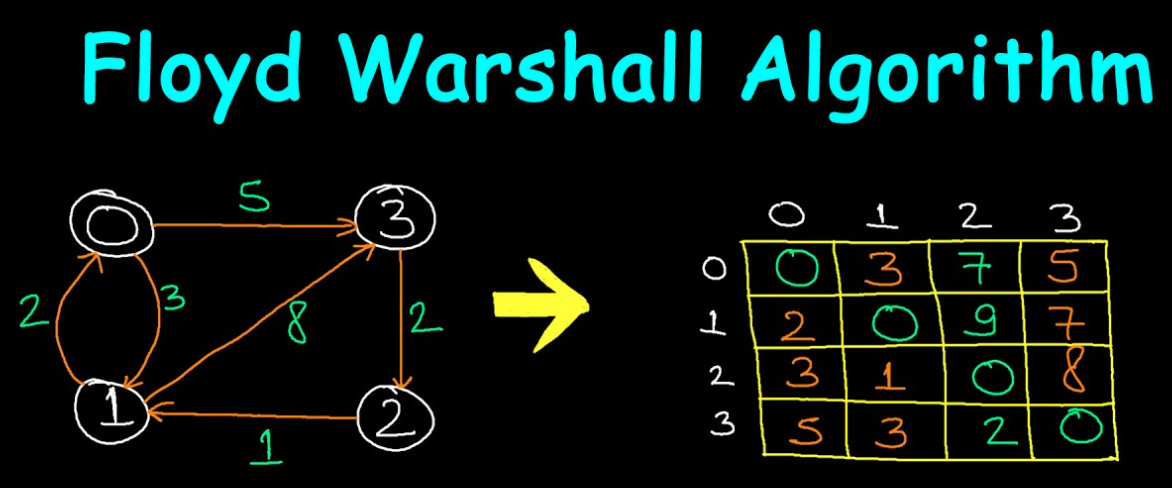
Floyd-Warshall算法正确性证明
从动态规划的角度证明 Floyd-Warshall 算法正确性。
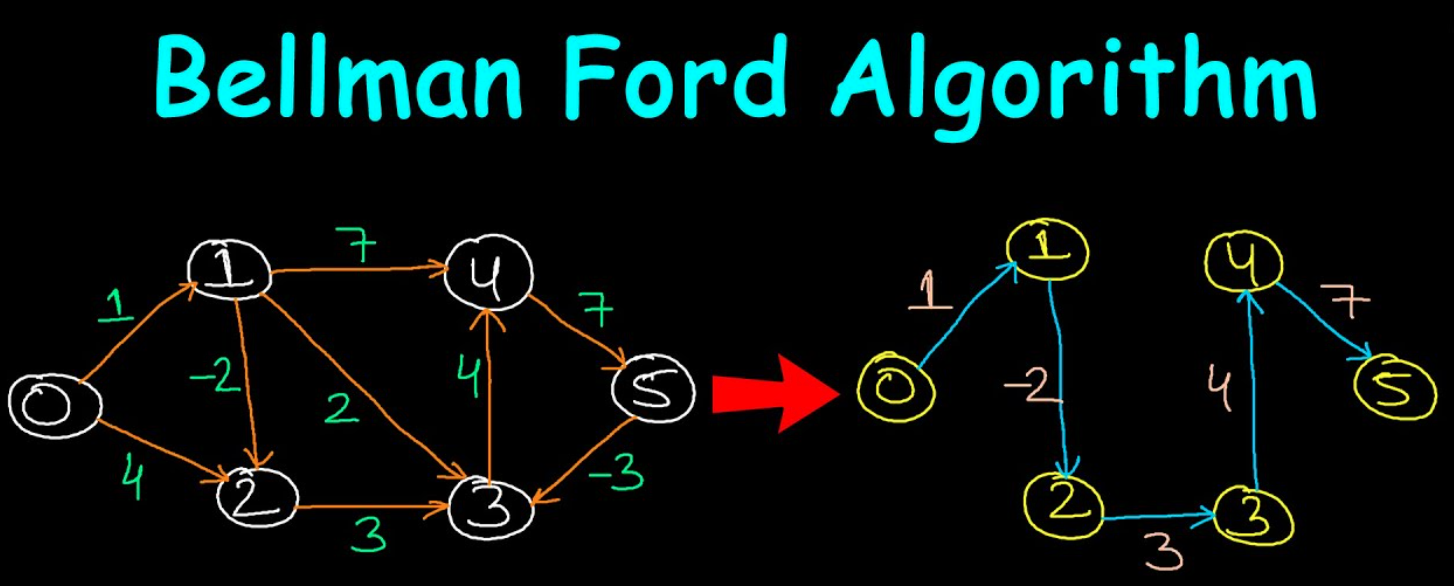
Bellman-Ford及SPFA算法正确性证明
从动态规划角度证明 Bellman-Ford 以及 SPFA 的正确性,并指出后者为何为前者的改进。
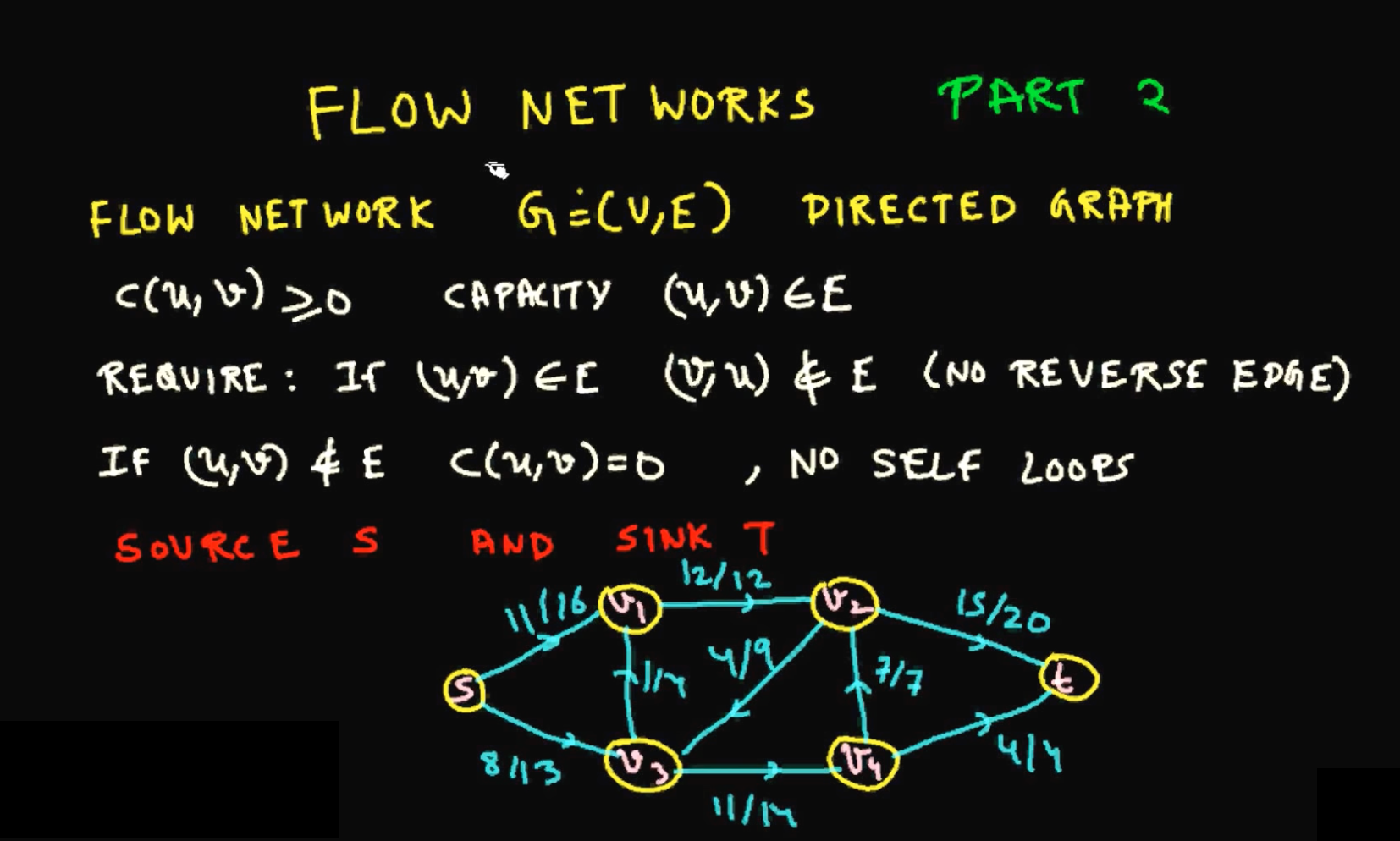
最大流最小割定理证明
详细证明最大流最小割定理,兼证明 Ford-Fulkerson 方法正确性。
Dijkstra算法正确性证明
用反证法严格证明 Dijkstra 算法。
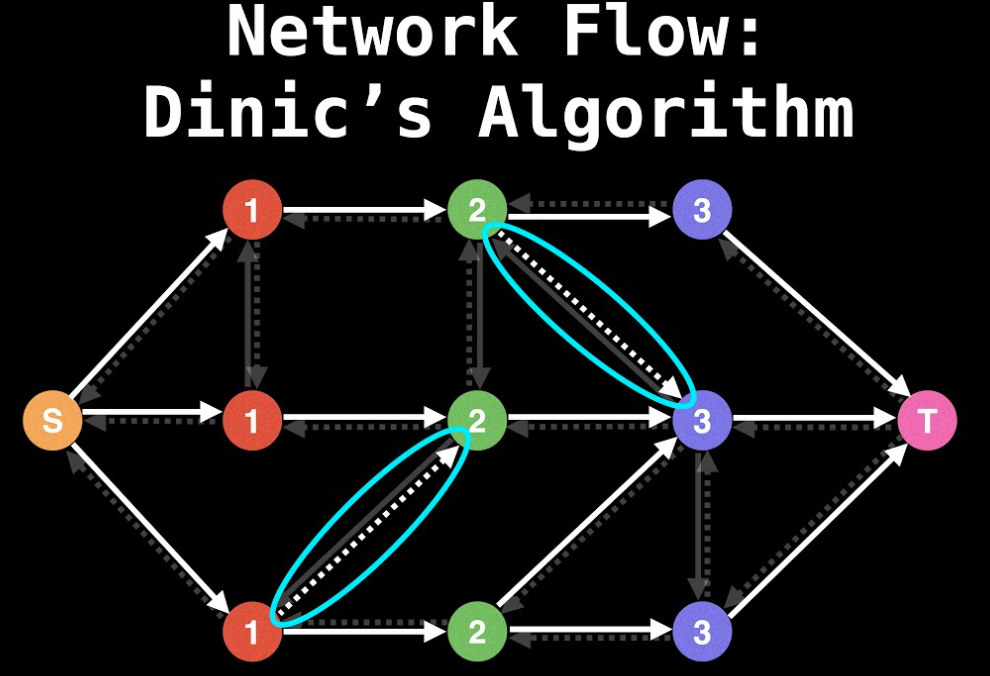
Dinic算法复杂度证明
证明 Dinic 算法时间复杂度为 O(|V|^2|E|) ,给出详细证明过程。
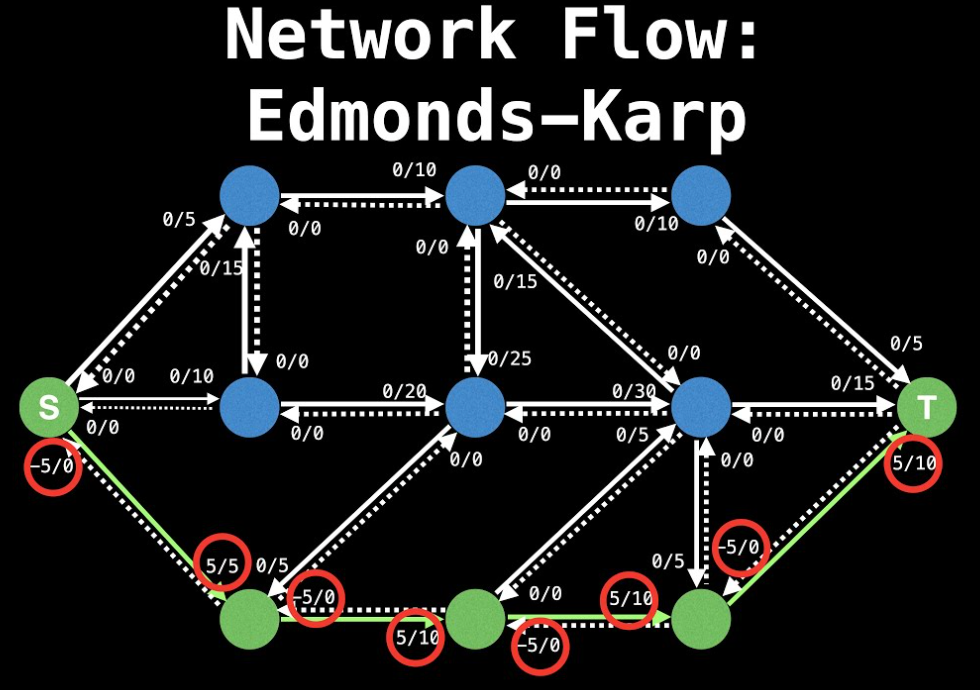
Edmonds-Karp算法复杂度证明
证明 Edmonds-Karp 算法时间复杂度为 O(|V||E|^2) ,给出详细证明过程。