Prim算法正确性证明

算法描述

Prim (普里姆算法): 一种基于贪心思想的求解无向图上 MST 的算法。我们直接将 Prim 算法和 Dijkstra 二者对比如下。

Dijkstra	Prim
贪心算法	贪心算法
顶点分为 距离已确定 和 距离未确定 顶点	顶点分为 距离已确定 (已加入生成树) 和 距离未确定 (未加入生成树) 顶点
所有顶点距离初始化为 $Infinity$	所有顶点距离初始化为 $Infinity$
源点 $s$ 的距离初始化为 0	生成树起始点 $s$ 的距离初始化为 0
以一个循环寻找 当前距离未确定顶点中距离最小者 $u$ ， 立即置 $u$ 的距离为「已确定」。	以一个循环寻找 当前距离未确定顶点中距离最小者 $u$ ， 立即置 $u$ 的距离为「已确定」。
尝试以如下方式更新 (松弛) $u$ 的邻接顶点的距离 $dv = min(dv, du + d(u, v))$	尝试以如下方式更新 $u$ 的邻接顶点的距离 $dv = min(dv, d(u,v))$
$while$ 结束时所有顶点最短路径及其距离被求出	$while$ 结束时 MST 及其所有边权被求出

我们看到这两个算法的每一步都几乎相同，不同点主要有三处，最主要的是第 3 点。

1. Prim 用于在「无向图」中求 MST，因此建图时要「双向建边」。Dijkstra 应用于有向图时单向建边，应用于无向图时双向建边。
2. Dijkstra 中的「距离」指的是顶点到源点的距离。Prim 中的「距离」指的是顶点到其已在生成树上的邻接顶点 (父顶点) 的距离。
3. 顶点距离更新方式不同 。

算法过程

1. 建图及初始化。

   1. 构建双向带权图。
   2. 设置一个大小为 $|V|$ 的用于标记顶点距离是否「已确定」的 $boolean$ 数组 $visited[]$ ，下标表示顶点。
   3. 设置一个大小为 $|V|$ 的距离数组 $dists[]$ ，下标表示顶点。初始化所有顶点的距离为 $Infinity$ ，表示所有顶点的距离尚未确定。
   4. 任意选取 一个顶点作为起始顶点，置距离为 0，通常我们将第一个顶点的距离置为 0 。

2. 以一个循环寻找 当前距离未确定顶点中距离最小者 $u$ ，立即置 $u$ 的距离为「已确定」。

3. 距离更新。尝试更新 $u$ 的所有 距离未确定的 邻接顶点 $v$ 的距离 $dv$。即 $dv = min\{dv, |(u,v)|\}$ 。

4. 循环结束时，所有顶点距离被求出，也就是 MST 所有边权被求出。

正确性证明

如下证明参考了 参考1 以及 参考2。

虽然 Prim 算法过程与 Dijkstra 类似，但证明过程并不通用。如下是 Prim 算法的证明过程。

证明：在图 $G$ 上执行 Prim 算法得到的生成树 $S$ 是 MST。

1. 记 $G$ 上的 MST (之一) 是生成树 $S_{min}$，即证明 $|S| = |S_{min}|$ ，绝对值表示生成树的边权和。
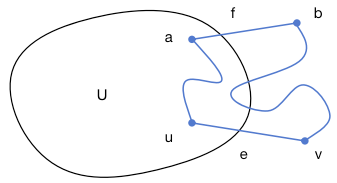
2. 在 $S$ 生长过程中，首次 遇到的不属于 $S_{min}$ 的边为 $e=(u, v)$ ，$u$ 在此前得到的点集中，$v$ 在剩余的顶点中。从 $S$ 中拿走 $e$ ，则 $S$ 剩下的不连通的两部分分别为包含 $u$ 的子树 $U$ 以及包含 $v$ 的子树 $V$ 。
3. $S_{min}$ 是 MST，其上必存在 $u$ 到 $v$ 的路径，且已知 $u$ 在 $U$ 中，$v$ 在 $V$ 中，由于 $(u,v)∉S_{min}$ ，则必然存在边 $f=(a,b)∈S_{min}$ 穿过 $U → V$，即 $a$ 在 $U$ 中， $b$ 在 $V$ 中 (若 $a$ 是 $u$ ，则 $b$ 不是 $v$；若 $b$ 是 $v$，则 $a$ 不是 $u$) 。
4. 当 $e$ 即将被加入 $S$ 时，顶点 $a$ 已在 $U$ 中 ( $U$ 是 $S$ 当前生长到的部分)。
   1. 此时 $a$ 是「距离未确定」的顶点。因为如果 $a$ 是距离已确定的顶点，则在 $U$ 中存在一条边 $g$ 连接 $a$ 和另一顶点，我们已经知道 $e$ 是 $S$ 生长过程中 首次 遇到的不属于 $S_{min}$ 的边，也就是说 $g∈S_{min}$ ，这与 $f∈S_{min}$ 矛盾，因为 $a$ 一旦「距离确定」，后续就不会考察 $a$ 的连边，$f$ 也就不可能加入 $S_{min}$ 。
   2. 由于 $a$ 是「距离未确定」的顶点，考察顶点 $u$ 的连边时，顶点 $a$ 的连边也一定会被考察。由于 $e$ 在此轮考察中被 Prim 算法选入 $S$ 中，而 $f$ 未被选择，可知 $|e|≤|f|$ 。
5. 对于 $S_{min}$ ，断开 $f=(a,b)$ ，则 $S_{min}$ 被分成不连通的两棵子树 $A$ 和 $B$，且 $u → a → b → v$ 被断开，说明 $u$ 与 $v$ 分别在不连通的两棵子树 $A, B$ 上。此时连上 $e=(u,v)$ 得到的 $S_{AeB}$ 显然是一棵生成树。因为 $|e|≤|f|$ ，则必然有 $|e|=|f|$ ， 否则 $S_{AeB}$ 边权之和更小，与 $S_{min}$ 是 MST 矛盾。因此 $|S_{AeB}|=|S_{min}|$，即 $S_{AeB}$ 也是 MST。
6. 重复上述过程，继续考察 $S$ 中下一条不属于 $S_{min}$ 的边，直到得到 $S$ 。每一次考察，都可以得到上述 5 的结论，最终有 $|S|=|S_{min}|$，即 $S$ 是 MST。