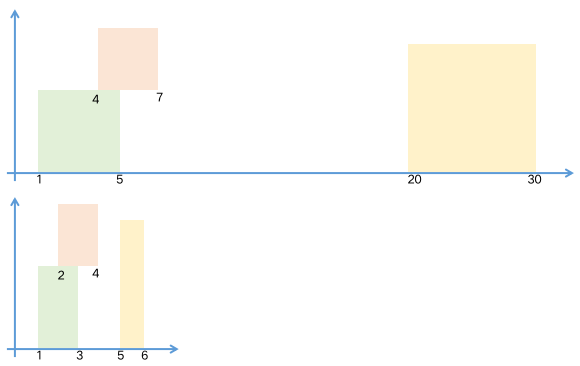线段树从入门到急停

感谢官方推荐 🎉😄。

  • 可在作者的 github仓库 中获取本文和其他文章的 markdown 源文件及相关代码。

  • 欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题，我将长期维护所有文章。

  • 所有文章均用 Typora 完成写作，可使用 Typora 打开文章 md 文件，以获得最佳阅读体验。

⚠️ ⚠️ ⚠️ 谨以此两万五千字文章献给在线段树门前徘徊的朋友。

❗️ 【NEW】最新文章如下 ❗️

这是小白 yuki 推出的「树ADT」系列文章的第 11 篇 (11/13) 。

keywordskeywords :

完全二叉树下标性质 / 分治算法 / 单点查询 (维护或不维护 numsnums) / 单点修改 (addadd & updateupdate) / (增量式 & 覆盖式) 区间修改 / 区间查询 (求和 & 求最值) / 堆式 (静态) 线段树 / 懒惰标记 / 延迟修改 / 离散化 (松离散 & 紧离散) / 强制在线 / 动态开点 / 结点数组法动态线段树 / 结点指针 (引用) 法动态线段树

线段树 是著名的用于高效求解 「区间问题」 的数据结构。「区间问题」即对于输入数组 numsnums ，在其上执行 「区间求和」 、 「区间修改」 等操作，通常还伴随着针对单个元素的 「单点查询」 、 「单点修改」 这两种单点操作。若直接操作 numsnums ，则单点操作时间复杂度为 O(1)O(1) ，而区间操作为 O(n)O(n) ；若采用「前缀和」，则区间操作为 O(1)O(1) ，而单点操作为 O(n)O(n) 。利用完全二叉树下标特点 (静态堆式线段树) 或动态开点操作 (动态线段树)，将 numsnums 上对任意元素值或任意区间值 (区间求和、区间最值等) 的求解，构建在一棵二叉树上，通过对该二叉树的分治处理 (dfsdfs) ，同时实现 O(logn)O(logn) 时间复杂度的单点操作与区间操作 。

本文行文过程中，我会将线段树与另一种求解区间问题的数据结构 –– 「树状数组」做对比。虽然「线段树」与「树状数组」在原理上差别不小，但 「区间划分」 的思想是一致的。「树状数组」的特点是思维难度大，实现简单，「线段树」正好相反，思维难度低，实现相对复杂，且对于区间问题，线段树比树状数组更具普适性。不过我仍然建议你在阅读本文之前先阅读 树状数组 一文，即便暂时理解不了树状数组中 lowbitlowbit 的作用也没关系，有了「树」与「区间问题」相联系的印象后，再学习本文的「线段树」，然后再返回去学习「树状数组」，效果也许更好（主要是我先写了「树状数组」再写的「线段树」😅）。

本文将给出 十种 线段树的完整类实现代码 (静态 & 动态)，可应对力扣中出现的 (几乎) 所有能用线段树解决的题目 。并在「实战应用」中给出近十道力扣上的线段树题目及详细题解 (持续增加中)。

另外，本文原题 「线段树 (树ADT连载 11/13)」，十分干瘪，不太符合作者的气质，遂改为现标题。「急停」表示作者的一种希望，我猜想许多朋友跟作者一样，在求索线段树的路上狼奔豕突，相关文章和题解看了不少，却始终不得其法。现在，作者希望朋友们能够通过本文实现完美急停，此后 从容吟啸且徐行。

yuki的其他文章如下，欢迎阅读指正！

如下所有文章同时也在我的 github 仓库 中维护。

文章 [发布时间] 字数/览/藏/赞 (~2022-10-20)
十大排序从入门到入赘 🔥🔥🔥 [20220516] 2.5万字/64.8k览/3.7k藏/937赞
二分查找从入门到入睡 🔥🔥🔥 [20220509] 2.3万字/38.4k览/2.1k藏/503赞
并查集从入门到出门 🔥🔥 [20220514] 1.2万字/17.9k览/1.0k藏/321赞
图论算法从入门到放下 🔥🔥 [20220617] 5.6万字/19.9k览/1.3k藏/365赞
树ADT系列 (预计13篇) 系列文章，连载中
3. 二叉查找树 [20220801] 5千字
4. AVL树 [20220817] 5千字
5. splay树 [20220817] 5千字
6. 红黑树从入门到看开 🔥🤯🤯🤯 [20220915] 3万字/5.3k览/269藏/72赞
10. 树状数组从入门到下车 🔥🤯 [20220722] 1.4万字/5.8k览/196藏/72赞
11. 线段树从入门到急停 🔥🤯 [20220726] 2.5万字/8.7k览/481藏/138赞
图论相关证明系列 系列文章
1. Dijkstra正确性证明 🤯 [20220531]
2. Prim正确性证明 🤯 [20220919]
3. Bellman-Ford及SPFA正确性证明 [20220602]
4. Floyd正确性证明 [20220602]
5. 最大流最小割定理证明 🤯🤯 [20220719]
6. Edmonds-Karp复杂度证明 🤯🤯 [20220515]
7. Dinic复杂度证明 🤯🤯 [20220531]

[2022-09-23]

[2022-09-22]

  • 增加了「区间最值查询」小节，替换了一张错误图片，另有若干词句修改。

[TOC]

线段树

我们已经知道，针对序列上的「区间操作」，相比普通数组和前缀和数组，基本树状数组 (PURQ BIT) 对「单点修改」及「区间查询」这两种操作实现了平衡，即均为 O(logn)O(logn) 时间复杂度。借助差分数组，从 PURQ BIT 发展而来的 RUPQ BIT (区间修改单点查询) 和 RURQ BIT (区间修改区间查询) 还可以实现 O(logn)O(logn) 复杂度区间修改操作，但需要针对不同的需要选择不同版本的树状数组。另外，当我们需要 将区间内元素修改为同一元素时 ，或者求给定区间的 区间最大/最小值 时，三种树状数组均不能以 O(logn)O(logn) 时间复杂度完成该操作。

对于这些需求，线段树都能够以 O(logn)O(logn) 时间复杂度完成 。

线段树 (Segment Tree): 线段树是一种用以支持序列区间操作的数据结构，相比基本树状数组，能够支持的操作种类更多，因此对一般的序列区间问题更具 普适性 。

在后续内容中，我们先通过 「完全二叉树下标性质」 和 「分治算法」 来理解基本线段树的工作原理。在掌握了支持「单点修改」和「区间查询」的基本线段树后，引入 「懒惰标记」 和 「延迟修改」 的概念，用以实现 「区间修改」。在给出带懒惰标记的线段树实现后，我们马上尝试解决 699. 掉落的方块 ，为解决此题需借用在「树状数组」中介绍过的 「离散化」 方法，我将给出 「松离散」 和 「紧离散」 两种离散化实现 (我自己瞎命名的)。接着尝试解决 715. Range 模块 ，并发现该题具有「强制在线」的特点，由于无法离散化，这要求我们实现能够 「动态开点」 (动态地创建结点) 的线段树。根据是否可以提前估计树的大小，我们将分别介绍 「结点数组法动态开点线段树」 以及 「结点指针 (引用) 法动态开点线段树」 ，在给出它们的完整的类代码后，演示如何将其用于解决 699 题以及 715 题。

在讲解过程中，我会给出十种线段树的完整类代码，基本能够覆盖力扣上的所有线段树题目。

线段树由 Jon Bentley 于1977年发明。

The segment tree was invented by Jon Bentley in 1977; in “Solutions to Klee’s rectangle problems”.[7]

作者的「线段树」知识，最初学自 OI wiki 线段树 。


基本线段树

如果我们只要求线段树像基本树状数组 (PURQ BIT) 那样只需支持「单点修改」和「区间查询」，那么我们将得到最基本的线段树。

在「树状数组」中我们从如何提高区间查询的效率这一问题入手，提出了将原数组 numsnums 分成若干子区间的想法，且这些子区间构成一棵逻辑树，通过树的结构实现 O(logn)O(logn) 的复杂度。但树状数组的实现太具技巧性，我们会想，除了树状数组利用 lowbitlowbit 那样巧妙构造树的方法，有没有 更一般 的方法能够将 numsnums 划分为多个子区间，这些子区间作为结点构成一棵树，树上的结点相比树状数组 更直观 地组成任意区间 (直接结合而非前缀区间作差)，且仍能通过下标的某些性质来操作结点呢 (目的是通过下标定位到需要的区间和结点) ？

根据树结点下标性质来操作结点这一要求中，我们嗅到了 「完全二叉树」 的味道。在完全二叉树中，结点 ii (根结点为结点 1) 的左子结点下标为 2∗i2*i ，右子结点下标为 2∗i+12*i+1 。顺着这个想法，我们尝试将「线段树」构造为一棵「完全二叉树」。


线段树的形态

假设需要在输入数组 numsnums 上求解区间问题，我们需要将 numsnums 处理为一棵「线段树」。下面是我们将「线段树」构造为一棵「完全二叉树」的思考过程。

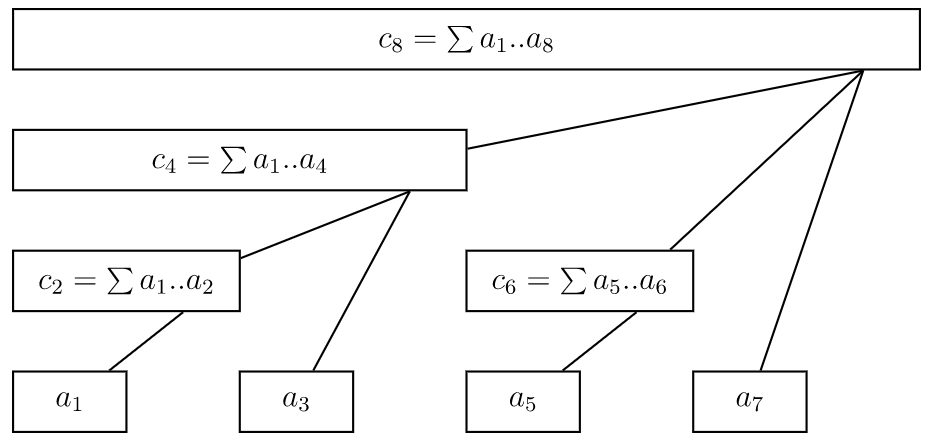
  • 首先，既然是完全二叉树，那么这棵线段树可以与一个数组对应，数组的一个元素对应一个树的一个结点。树的一个结点代表某个区间的区间和，我们用 tree[]tree[] 数组表达这棵线段树，其大小暂时未知。

  • 更大的区间总是由更小区间构成，因此代表 numsnums 中单个元素的结点 tree[x]tree[x] 应当在树的最底层 ，即线段树的每一个叶子结点都与 numsnums 中的一个值对应 tree[x]=nums[i]tree[x] = nums[i] ，且是从左到右对应的。

  • 更大的区间是从叶子结点开始向上构成的，例如代表 nums[0]nums[0] 的叶子结点是一个左子结点，代表 nums[1]nums[1] 的叶子结点是一个右子结点，那么他们的父节点即为代表区间 [0,1][0,1] 的结点。

  • 查询区间 [l,r][l,r] 的区间和，总是从上到下查询。从根结点开始，为了知道指定区间包含哪些区间结点，需要将 l,rl,r 与结点的标号联系起来，也就是将 numsnums 的下标与 形如完全二叉树的线段树的结点标号 相联系，这个「完全二叉树结点下标性质」我们很熟悉，将数组 numsnums 看作完全二叉树时，树的结点代表 numsnums 中的某个值， 而在线段树中，树的结点代表 numsnums 中的某段区间和。

在熟知完全二叉树下标性质的基础上，上述分析是简单的。tree[i]tree[i] 表示标号为 ii 的结点所代表的区间的区间和。令根结点标号为 1。根结点 tree[1]tree[1] 代表整个 numsnums 所有元素之和。很自然地，根结点的左右子结点应当代表左右两半区间的区间和，即 tree[2]tree[2] 表示区间 [0,n−12][0, \frac{n-1}{2}] 的区间和，tree[3]tree[3] 表示区间 [n−12+1,n−1][\frac{n-1}{2}+1, n-1] 的区间和，依次向下， 结点标号总是与该结点代表的区间一一对应 。

代表区间 [l,r][l,r] 的结点 tree[i]tree[i] ，其左子结点 tree[2∗i]tree[2*i] 表示区间 [l,l+r2][l,\frac{l+r}{2}] 的区间和；其右子结点 tree[2∗i+1]tree[2*i+1] 表示区间 [l+r2+1,r][\frac{l+r}{2}+1,r] 的区间和。

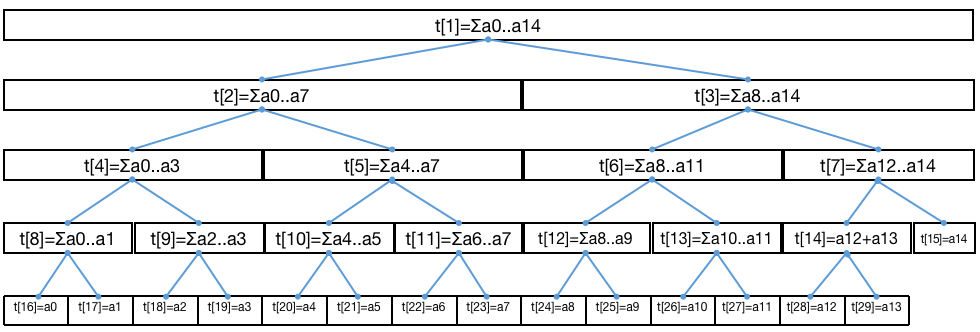
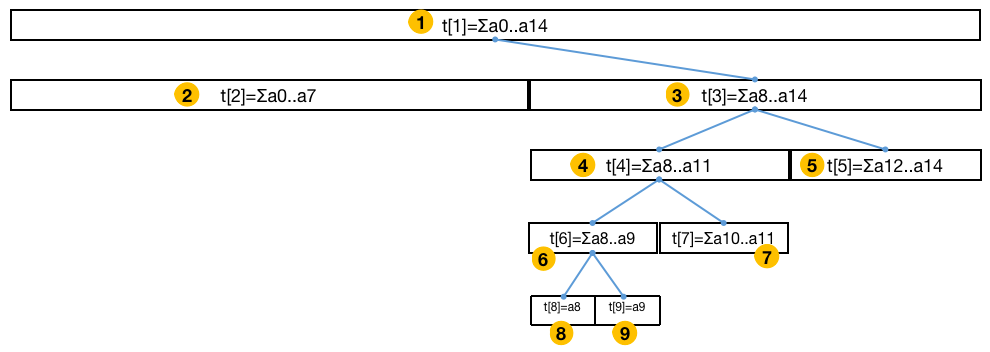
于是我们很容易得到线段树的一般表示，下图表示大小为 15 的 nums={a0,a1,...,a14}nums=\{a0,a1,...,a14\} 对应的线段树。可以看到，对于任意区间 [l,r],l,r∈[0,n−1][l,r], l,r∈[0,n-1] ，我们都可以由 ll 到 rr 的若干个子区间组合得到，这一点是线段树与树状数组的显著区别 (树状数组通过两个前缀区间作差得到)。

image.png

了解了线段树的区间划分、结点所代表的具体区间与结点下标的关系后，接下来我们给出基本线段树的「初始化」、「单点修改」以及「区间查询」实现。在这之前先简单分析线段树的大小。


线段树的大小

对于长度为 nn 的输入数组 numsnums ，初始化它所对应的线段树前 (即 tree[]tree[] 数组)，我们需要知道 tree[]tree[] 的大小。nn 对应的是线段树叶子结点数，我们设总结点数为 mm ，可以 根据线段树为一棵完全二叉树的特点来寻找 nn 与 mm 的关系 。证明见 oi-wiki 线段树 ，作者未完全看懂 mm 最大时为 m=4∗n−5m=4*n-5 的证明过程。如果读者能提供易懂的数学证明，盼赐教。

总之，在实际使用时，我们总是不精确地令 m=4∗nm=4*n 。


初始化

如果读者熟悉归并排序和快速排序这类 分治算法 的「对原问题域递归地划分为左右子问题域」的操作，那么线段树的主要方法都将是简单的。我们直接给出如下线段树类 SegmentTreeSegmentTree 的构造器代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class SegmentTree {
    int[] nums, tree;
    int n;
    public SegmentTree(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n]; // 线段树结点数不超过 4*n
        build(0, n - 1, 1);
    }
    private void build(int s, int t, int i){ // 构建线段树(tree数组), i: 当前区间结点下标
        if(s == t) { // s: start,nums当前区间左界，t: terminal,nums当前结点区间右界
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
}

构造器通过 build(0, n - 1, 1) 完成线段树的构建 (初始化 tree[]tree[])。在 buildbuild 中，自根结点往下，按照我们在「线段树的形态」中所说的那样，递归地将 numsnums 分为左右两半，直到叶子结点，每次递归， 区间和结点的下标总是和该区间的左右界一起被传入 。该写法实际上就是大家十分熟悉的二叉树的「后序遍历」写法。

递归的基准情形是根据 s == t 判断到达叶子结点后，令 tree[i] = nums[s] ，使得每个叶子结点从左到右对应 numsnums 的每个元素值。在回溯过程中通过 tree[i] = tree[i * 2] + tree[i * 2 + 1] 自底向上地初始化所有区间结点的区间和。这行语句在线段树的实现中较常用，我们可以将它封装为一个辅助方法 pushUppushUp 。

1
2
3
4
// 更新 tree[i]
private void pushUp(int i){ 
    tree[i] = tree[i * 2] + tree[i * 2 + 1];
}

后面我们将看到，线段树的所有主要方法的执行过程，都是类似这样的 二叉树后序遍历的递归过程 ，读者一定会感到线段树不同方法的写法如出一辙，简单得令人惊讶。


单点修改

单点修改有两种，增量式修改，即加上某值 (记为 addadd 方法) nums[i]+=xnums[i]+=x 或 覆盖式修改，即改为某值 (记为 updateupdate 方法) nums[i]=xnums[i]=x。如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 单点修改(驱动): nums[i] += x
public void add(int i, int x){ 
    add(i, x, 0, n - 1, 1);
}
// 单点修改(驱动): nums[i] = x
public void update(int i, int x){
    update(i, x, 0, n - 1, 1);
}
// 单点修改: nums[idx] += x
private void add(int idx, int x, int s, int t, int i){
    if(s == t) {
        tree[i] += x; // 增量更新
        return;
    }
    int c = s + (t - s) / 2;
    if(idx <= c) add(idx, x, s, c, i * 2);
    else add(idx, x, c + 1, t, i * 2 + 1);
    pushUp(i);
}
// 单点修改: nums[idx] = x
private void update(int idx, int x, int s, int t, int i){
    if(s == t) {
        tree[i] = x; // 覆盖更新
        return;
    }
    int c = s + (t - s) / 2;
    if(idx <= c) update(idx, x, s, c, i * 2);
    else update(idx, x, c + 1, t, i * 2 + 1);
    pushUp(i);
}

addadd 和 updateupdate 均采用上述写法时，可以不用维护 numsnums ，由于 numsnums 不可用，单点查询可实现如下。

1
2
3
4
5
6
7
8
9
10
11
// 单点查询 (驱动): 查询 nums[i]
public int query(int i){ 
    return query(i, 0, n - 1, 1);
}
// 单点查询 (具体): 查询 nums[i]，尾递归
private int query(int idx, int s, int t, int i){
    if(s == t) return tree[i];
    int c = s + (t - s) / 2;
    if(idx <= c) return query(idx, s, c, i * 2);
    else return query(idx, c + 1, t, i * 2 + 1);
}

当然我们也可以实时地维护 numsnums ，那么 addadd 写法不变， updateupdate 可借助 addadd 实现。由于 nums[i]nums[i] 是实时维护的，单点查询时直接返回 nums[i]nums[i] 即可。

1
2
3
4
5
6
7
8
// 单点修改(驱动): nums[i] = x
public void update(int i, int x){ 
    add(i, x - nums[i], 0, n - 1, 1);
    nums[i] = x; // 实时维护 nums[i]
}
public int query(int i){ // 单点查询: 查询 nums[i]
    return nums[i];
}

实际上，由于单点查询和单点修改都可以视作区间长度为 1 的区间查询和区间修改。上述方法也可以由区间查询和区间修改代替。


区间查询

区间查询 (求和) 也是简单的。与单点操作不同的是，区间和需要累积，因此 if(l <= c) 与 if(r > c) 是并列关系。递归的基准情形为 if(l <= s && t <= r) ，表示当前递进到的区间 [s,t][s,t] 在所求区间 [l,r][l,r] 之内，返回该区间的区间和 tree[i]tree[i] 用于累计。

1
2
3
4
5
6
7
8
9
10
11
12
// 区间查询(驱动): nums[l]~nums[r]之和
public int sum(int l, int r){ 
    return sum(l, r, 0, n - 1, 1);
}
// 区间查询: nums[l]~nums[r]之和
private int sum(int l, int r, int s, int t, int i){
    if(l <= s && t <= r) return tree[i]; // 当前结点区间在所求范围之间
    int c = s + (t - s) / 2, sum = 0;
    if(l <= c) sum += sum(l, r, s, c, i * 2); // 递归累加目标区间落在c左侧(含c)的区间和
    if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1); // 递归累加目标区间落在c右侧的区间和
    return sum;
}

也可以查询区间最值，以区间最小值为例，如下。

1
2
3
4
5
6
7
8
9
10
11
12
// 区间查询 (驱动): 查询[l,r]中的最小值
public int min(int l, int r){ 
    return min(l, r, 0, n - 1, 1);
}
// 区间查询: 查询[l,r]中的最小值
private int min(int l, int r, int s, int t, int i){
    if(s == t) return tree[i]; // 叶子结点
    int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
    if(l <= c) lmin = min(l, r, s, c, i * 2);
    if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
    return Math.min(lmin, rmin);
}

区间最值查询

需要注意的是，对于「区间最值查询」，上面给出的 minmin 方法建立在 tree[]tree[] 的定义为「区间和」基础之上。在这个定义下，由于缺乏子区间最值的记录，为了找到最值， minmin , maxmax 方法最终会递进到区间内的每一个叶子结点，如果查询的是整个问题区间上的最值，那就相当于经历一次完整的树的 dfsdfs 遍历，所以平均时间复杂度是 O(n)O(n) 。若要实现 O(logn)O(logn) 复杂度的「区间最值查询」，做法是令 tree[]tree[] 记录区间最值 而不是区间和。以 tree[]tree[] 记录区间最值的典型线段树题目是 699. 掉落的方块 一题，详细做法请参考 题解 。其中求区间最大值的代码如下，可以看到，与 tree[]tree[] 定义为「区间和」时的「区间求和查询」的 sumsum 方法十分类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// tree[] 定义为区间最大值时，可实现 O(logn) 时间复杂度的区间最值查询。

// 区间查询 (驱动): 查询[l,r]中的最大值
public int max(int l, int r){ 
    return max(l, r, 0, n - 1, 1);
}
// 区间查询: 查询[l,r]中的最大值
private int max(int l, int r, int s, int t, int i){ 
    if(l <= s && t <= r) return tree[i]; // 当前区间是否包含在所求区间中
    int c = s + (t - s) / 2, lmax = 0, rmax = 0;
    if(lazy[i] != 0) pushDown(s, c, t, i);
    if(l <= c) lmax = max(l, r, s, c, i * 2);
    if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
    return Math.max(lmax, rmax);
}

另外要注意由于 tree[]tree[] 的意义是区间最值，因此 pushUppushUp 方法也与之前不同，应如下。

1
2
3
4
// pushup: 更新 tree[i]
private void pushUp(int i){
    tree[i] = Math.max(tree[i * 2], tree[i * 2 + 1]);
}

对于后续其他版本的线段树，只需将 tree[]tree[] 定义为记录「区间最大值」，相应地完成上述两处修改，即可得到以 O(logn)O(logn) 时间复杂度完成「区间最大值查询」的线段树。同样地，若想得到以 O(logn)O(logn) 时间复杂度完成「区间最小值查询」的线段树，就将 tree[]tree[] 定义为记录「区间最小值」。但是要注意，因为 tree[]tree[] 不再记录「区间和」，则 sumsum 方法求区间和需要递进到每一个叶子结点，此时 sumsum 方法的时间复杂度是 O(n)O(n) 。

我们看到，无论 tree[]tree[] 的定义是什么，当需要单个叶子结点信息时，基准情形应写为 if(s == t) return tree[i]; ，当需要包含于所求区间的当前区间信息时，基准情形为 if(l <= s && t <= r) return tree[i]; 。

在下面的「类的实现代码」中，只展示「不维护 numsnums 的以 O(logn)O(logn) 时间复杂度完成区间最大值查询的基本静态线段树」的完整类代码，其他版本读者可以自己写出。

若要求线段树以 O(logn)O(logn) 时间复杂度同时支持「区间和查询」、「区间最大值查询」以及「区间最小值查询」，只需要同时维护三个树结点值数组即可，treeSum[],treeMax[],treeMin[]treeSum[],treeMax[],treeMin[] 分别用来记录区间和、区间最大值以及区间最小值，并简单修改相关代码即可。完整实现是「类的实现代码」中的「区间查询扩展版本」。


类的实现代码

将前述方法的实现代码组合起来即可 (实时维护 numsnums 或不维护 numsnums 两个版本)，见后。

不过，我们在一开始说过线段树能很好地支持「区间修改」操作，为什么还没提供相关方法就在这里给出类的代码呢？这是因为，与树状数组 (RUPQ/RURQ BIT) 区间修改时只需要在 addadd 中沿着父链修改 O(logn)O(logn) 次不同， 线段树修改一段区间自上而下涉及到一个或多个子树空间内所有结点的修改 。例如若修改整个 numsnums ，那么就要从根结点 dfsdfs 整棵树，修改涉及 所有结点 ，时间复杂度为 O(n)O(n) 。对于随机区间来说，平均时间复杂度为 O(n)O(n) ，且由于所有区间结点的数量大于 nn (通常设置为 4n4n)，这样的操作甚至劣于直接遍历 numsnums 逐个修改。

为了解决这个问题，我们不是直接 dfsdfs 修改，而是通过一种称为 「懒惰标记」 的技巧，使子树中的修改操作 延迟 到后续修改和查询操作中，此技巧使得区间修改的时间复杂度仍为 O(logn)O(logn) 。

为了更稳固地学习后续内容，建议读者先基于目前为止讲解的内容尝试解决 307. 区域和检索 - 数组可修改 ，代码可参考「实战应用」一节给出的题解。


实时维护nums的版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/**
 * 基本线段树1 (无懒标记，无区间修改方法，实时维护 nums[i])
 * 支持：单点修改 / 单点查询 / 区间查询
 */
class SegmentTreeBasic1 {
    int[] nums, tree;
    int n;
    public SegmentTreeBasic1(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){ // 单点修改(驱动): nums[i] = x
        add(i, x - nums[i], 0, n - 1, 1);
        nums[i] = x; // 实时维护 nums[i]
    }
    public int query(int i){ // 单点查询: 查询 nums[i]
        return nums[i];
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点修改: nums[idx] += x
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // 区间查询: nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i]; // 当前结点区间在所求范围之间
        int c = s + (t - s) / 2, sum = 0;
        if(l <= c) sum += sum(l, r, s, c, i * 2); // 递归累加目标区间落在c左侧(含c)的区间和
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1); // 递归累加目标区间落在c右侧的区间和
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i]; // 叶子结点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(l <= c) lmin = min(l, r, s, c, i * 2);
        if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前区间起点下标，t: terminal,nums当前结点区间末尾下标
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // pushup: 更新 tree[i]
    private void pushUp(int i){
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
}

不维护nums的版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
/**
 * 基本线段树2 (无懒标记，无区间修改方法，不维护 nums[i])
 * 支持：单点修改 / 单点查询 / 区间查询
 */
class SegmentTreeBasic2 {
    int[] nums, tree;
    int n;
    public SegmentTreeBasic2(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){// 单点修改(驱动): nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2;
        if(idx <= c) return query(idx, s, c, i * 2);
        else return query(idx, c + 1, t, i * 2 + 1);
    }
    // 单点修改: nums[idx] += x
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // 单点修改: nums[idx] = x
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] = x; // 覆盖更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) update(idx, x, s, c, i * 2);
        else update(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // 区间查询: nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i]; // 当前结点区间在所求范围之间
        int c = s + (t - s) / 2, sum = 0;
        if(l <= c) sum += sum(l, r, s, c, i * 2); // 递归累加目标区间落在c左侧(含c)的区间和
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1); // 递归累加目标区间落在c右侧的区间和
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i]; // 叶子结点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(l <= c) lmin = min(l, r, s, c, i * 2);
        if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前区间起点下标，t: terminal,nums当前结点区间末尾下标
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // pushup: 更新 tree[i]
    private void pushUp(int i){
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
}

O(logn)时间求区间最大值版本

以下是不维护 numsnums 的以 O(logn)O(logn) 时间复杂度完成 「区间最大值查询」 的基本静态线段树类实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
/**
 * 区间最大值基本线段树 (无懒标记，无区间修改方法，不维护 nums[i])
 * 支持：单点修改 / 单点查询 / 区间查询最大值
 */
class SegmentTreeBasicRangeMax {
    int[] nums, tree;
    int n;
    public SegmentTreeBasicRangeMax(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){// 单点修改(驱动): nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2;
        if(idx <= c) return query(idx, s, c, i * 2);
        else return query(idx, c + 1, t, i * 2 + 1);
    }
    // 单点修改: nums[idx] += x
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // 单点修改: nums[idx] = x
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] = x; // 覆盖更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) update(idx, x, s, c, i * 2);
        else update(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // 区间查询: nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(s == t) return tree[i]; // 返回所求范围内的叶子结点的值
        int c = s + (t - s) / 2, sum = 0;
        if(l <= c) sum += sum(l, r, s, c, i * 2); // 递归累加目标区间落在c左侧(含c)的区间和
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1); // 递归累加目标区间落在c右侧的区间和
        return sum;
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前区间起点下标，t: terminal,nums当前结点区间末尾下标
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUp(i);
    }
    // pushup: 更新 tree[i]
    private void pushUp(int i){
        tree[i] = Math.max(tree[i * 2], tree[i * 2 + 1]);
    }
}

区间查询扩展版本

以 O(logn)O(logn) 时间复杂度同时支持「区间和查询」、「区间最大值查询」以及「区间最小值查询」的基本静态线段树类实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
/**
 * 基本线段树 (无懒标记，无区间修改方法，不维护 nums[i])
 * 支持：单点修改 / 单点查询 / 区间查询 (同时支持 O(logn) 时间的区间和，区间最大值，区间最小值查询)
 */
class SegmentTreeBasic {
    int[] nums, treeSum, treeMin,treeMax;
    int n;
    public SegmentTreeBasic(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.treeSum = new int[4 * n];
        this.treeMin = new int[4 * n];
        this.treeMax = new int[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){// 单点修改(驱动): nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return treeSum[i];
        int c = s + (t - s) / 2;
        if(idx <= c) return query(idx, s, c, i * 2);
        else return query(idx, c + 1, t, i * 2 + 1);
    }
    // 单点修改: nums[idx] += x
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            treeSum[i] += x; // 增量更新
            treeMin[i] += x; // 增量更新
            treeMax[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUpSum(i);
        pushUpMin(i);
        pushUpMax(i);
    }
    // 单点修改: nums[idx] = x
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            treeSum[i] = x; // 覆盖更新
            treeMin[i] = x; // 覆盖更新
            treeMax[i] = x; // 覆盖更新
            return;
        }
        int c = s + (t - s) / 2;
        if(idx <= c) update(idx, x, s, c, i * 2);
        else update(idx, x, c + 1, t, i * 2 + 1);
        pushUpSum(i);
        pushUpMin(i);
        pushUpMax(i);
    }
    // 区间查询: nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return treeSum[i]; 
        int c = s + (t - s) / 2, sum = 0;
        if(l <= c) sum += sum(l, r, s, c, i * 2); // 递归累加目标区间落在c左侧(含c)的区间和
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1); // 递归累加目标区间落在c右侧的区间和
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return treeMin[i];
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(l <= c) lmin = min(l, r, s, c, i * 2);
        if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return treeMax[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前区间起点下标，t: terminal,nums当前结点区间末尾下标
            treeSum[i] = nums[s];
            treeMin[i] = nums[s];
            treeMax[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUpSum(i);
        pushUpMin(i);
        pushUpMax(i);
    }
    // pushUpSum: 更新 treeSum[i]
    private void pushUpSum(int i){
        treeSum[i] = treeSum[i * 2] + treeSum[i * 2 + 1];
    }
    // pushUpMin: 更新 treeMin[i]
    private void pushUpMin(int i){
        treeMin[i] = Math.min(treeMin[i * 2], treeMin[i * 2 + 1]);
    }
    // pushUpMax: 更新 treeMax[i]
    private void pushUpMax(int i){
        treeMax[i] = Math.max(treeMax[i * 2], treeMax[i * 2 + 1]);
    }
}

懒惰标记

回顾一下前述 sumsum 方法，给定区间 [l,r][l,r] ，当方法递归到一个完全位于 [l,r][l,r] 的 [s,t][s,t] 区间 (即 l <= s && t <= r ) 时，我们直接累积该区间的区间和。可见，区间查询时，只要当前区间完全处于查询区间之内，我们就不需要知道此区间以下的区间的信息。因此对于区间查询 (求和) 操作，时间复杂度是 O(logn)O(logn) ，那么「区间修改」该如何实现呢？思考与区间查询类似的做法，区间修改方法从根结点递进到一个 包含于修改区间之内的区间 时，是否可以 只修改代表该区间的区间和 ，而不必继续深入修改它的子区间的区间和呢？因为若修改区间下的子区间 (子树空间) 都要修改的话，相当于树的遍历，时间复杂度为 O(n)O(n) ，而我们想要实现时间复杂度为 O(logn)O(logn) 的区间修改。下面我们仔细分析这一做法。

因为递归方法总是同时传入结点下标 ii 及该结点代表区间的左右界 [s,t][s,t] ，因此可以通过 if(l <= s && t <= r) 来判断当前结点代表的区间是否完全包含于 [l,r][l,r] 的区间内，若包含，由于知道左右界信息，因此可以直接更新 tree[i]tree[i] 。此后查询包含 [s,t][s,t] 的区间 [l,r][l,r] ，dfsdfs 递进到代表 [s,t][s,t] 区间的结点 tree[i]tree[i] 时，tree[i]tree[i] 总是正确的。但如果 [l,r][l,r] 值只覆盖了一部分 [s,t][s,t] ，就必须从 tree[i]tree[i] 结点继续向下访问 [s,t][s,t] 的子区间，而先前我们并没有将区间修改进行到子区间，因此查询将得不到正确结果。

解决办法是在前一次修改 [s,t][s,t] 的 tree[i]tree[i] 值时，另外使用一个与 tree[]tree[] 等大的 lazy[]lazy[] 数组标记此时的修改 (修改 lazy[i]lazy[i] )，以便于下次查询到 tree[i]tree[i] 时 将这个修改传递给子区间 。我们将这个动作称为 「延迟修改」 ，将这个标记形象地称作 「懒惰标记」 。不好理解？没关系，我们马上结合示意图与代码来跟踪相关操作。


区间修改 (增量式)

我们先分析 为区间内所有元素增加同一值的「增量式区间修改」 操作。

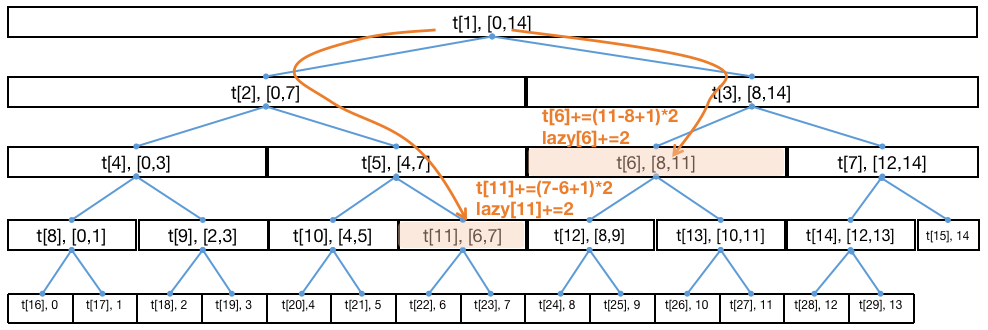
如下图，执行 add(6, 11, 2) 为区间 [6,11][6,11] 的每个元素都加上 2 。 递归调用到 tree[6]tree[6] 以及 tree[11]tree[11] 时 (暂时忽略递进到此处之前的操作)，会分别执行 tree[6] += (11 - 8 + 1) * 2 和 tree[11] += (7 - 6 + 1) * 2 。同时，增量 2 也会被 lazy[6]lazy[6] 和 lazy[11]lazy[11] 记录。由于 标记可能还记录了前面的修改，而修改是增量式的，因此需累加 ，即 lazy[6] += 2 及 lazy[11] += 2。

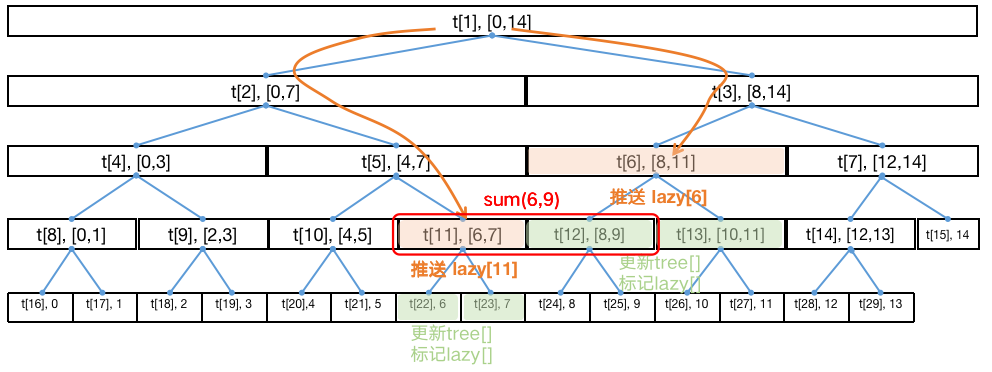
image.png

接着，我们查询 [6,9][6,9] 的区间和 ( sum(6,9)sum(6,9) )，递进访问到 tree[6]tree[6] 结点时，要将懒标记记录的修改量 lazy[6]lazy[6] 传递给 tree[12]tree[12] 和 tree[13]tree[13] 。同样地，访问到 tree[11]tree[11] 结点时，要将懒标记记录的修改量 lazy[11]lazy[11] 传递给 tree[22]tree[22] 和 tree[23]tree[23] 。 「推送」 指的是通过 pushDownpushDown 方法完成 当前区间以及它的两个子结点区间的区间和以及懒标记的更新 。

image.png

现在我们很容易理解下面的实现代码。private void add 方法中，当递进到所代表的区间完全包含于 [l,r][l,r] 内的 tree[i]tree[i] 结点时 (代表区间 [s,t][s,t] )，我们执行 tree[i] += (t - s + 1) * x 语句更新 tree[i]tree[i] ，接着执行 if(s != t) lazy[i] += x 后返回。懒标记更新前的判断使得 叶子结点不会被标记 ，因为 叶子结点之下不再有需要推送标记的结点 。当然也可以不用判断，因为无论是查询还是修改，到达叶子结点时一定会进入方法开始的 ifif 语句后通过 returnreturn 返回，叶子结点没有向下推送的机会。

if(lazy[i] != 0) pushDown(s, c, t, i) 表示在递归进入左右子结点前，检查当前 tree[i]tree[i] 顶点值是否要向下推送标记，lazy[i] != 0 说明当前 tree[i]tree[i] 有 尚未推送的修改 ，需要在这个时候推送到下一层，否则递归进入左右子结点时，左右子结点的区间和是旧的。

pushDownpushDown 方法传入 s,c,t,is,c,t,i ，用于更新 tree[i]tree[i] 的左子结点区间和 tree[2∗i]tree[2*i] 、右子结点区间和 tree[2∗i+1]tree[2*i+1] 以及它们的懒标记。更新结束后 tree[i]tree[i] 结点的「推送修改量」的任务就完成了，需要将其懒标记设置为 0 ，即 lazy[i] = 0 ，否则下次修改或查询再经过 tree[i]tree[i] 时，会重复推送。

addadd 方法的最后一行调用 pushUppushUp 方法，这是递归的 「后序」 动作，回溯过程中自底向上更新递进路径上的 tree[i]tree[i] 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 区间修改(驱动): [l,r]区间所有元素加上x
public void add(int l, int r, int x){ 
    add(l, r, x, 0, n - 1, 1);
}
// 区间修改: 增量式 [l,r] 区间所有元素加上x
private void add(int l, int r, int x, int s, int t, int i){ 
    if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
        tree[i] += (t - s + 1) * x; // 结点i的区间和加上t-s+1个x
        if(s != t) lazy[i] += x; // 结点i不是叶子结点，懒标记值加上x
        return;
    }
    int c = s + (t - s) / 2;
    if(lazy[i] != 0) pushDown(s, c, t, i); // 当前结点懒惰标记不为0，推送标记
    if(l <= c) add(l, r, x, s, c, i * 2);
    if(r > c) add(l, r, x, c + 1, t, i * 2 + 1);
    pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
}
// 更新结点i左右子结点的区间和以及懒惰标记值，最后重置结点i的懒惰标记值
private void pushDown(int s, int c, int t, int i){ 
    tree[i * 2] += (c - s + 1) * lazy[i]; // 更新其左子结点的区间和
    lazy[i * 2] += lazy[i]; // 传递懒标记(增量标记)
    tree[i * 2 + 1] += (t - c) * lazy[i];
    lazy[i * 2 + 1] += lazy[i];
    lazy[i] = 0; // 重置当前结点懒惰标记值（增量标记置0）
}
// 更新 tree[i]
private void pushUp(int i){ 
    tree[i] = tree[i * 2] + tree[i * 2 + 1];
}

区间修改 (覆盖式)

接着分析 将区间内所有元素修改为同一值的「覆盖式区间修改」 操作。与单点覆盖式修改方法可以通过调用单点增量式修改方法来实现不同，由于 涉及多个值的修改 ，区间覆盖式修改不能通过调用区间增量式方法来实现。且覆盖式修改可能将 numsnums 的原元素值改为 0，因此不能再以 lazy[i] != 0 来作为推送标记的标志。我们可以创建一个新的 boolean updated[] 数组来记录结点 ii 当前的修改状态，若 updated[i] == true 说明结点 ii 的 覆盖式修改未推送 。需注意的是， pushDownpushDown 方法也需要若干调整。如下是区间覆盖式修改的相关代码实现，与增量式区间修改代码的区别仅仅是用 if(updated[i]) 代替了 if(lazy[i] != 0) ，以及将「增量赋值」的 += 改为「覆盖赋值」 = ，以及相应的 updated[i]updated[i] 的设置和更新。

如果我们能确定覆盖式区间修改不会将元素值改为 0 的话，那 updated[]updated[] 数组不是必须的，仍可用 lazy[i]lazy[i] 是否为 0 作为判断条件，这种情况下增量式与覆盖式的代码将十分相似，几乎只有 += 和 = 的区别。例如 699. 掉落的方块 一题，需要实现覆盖式区间修改，但题目保证了修改值不会是 0 ，实现代码就不需要另外使用 boolean updated[] ，具体请看「实战应用」中该题 题解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 区间修改(驱动): 覆盖式 [l,r] 区间所有元素改为x
public void update(int l, int r, int x){ 
    update(l, r, x, 0, n - 1, 1);
}
// 区间修改: 覆盖式 [l,r] 区间所有元素改为x
private void update(int l, int r, int x, int s, int t, int i){ 
    if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
        tree[i] = (t - s + 1) * x; // 结点i的区间和等于t-s+1个x
        if(s != t) { // 结点i不是叶子结点
            lazy[i] = x; // 懒标记值等于x
            updated[i] = true; // updated[i]置于为为true
        }
        return;
    }
    int c = s + (t - s) / 2;
    if(updated[i]) pushDown(s, c, t, i); // 当前结点updated为true，推送标记
    if(l <= c) update(l, r, x, s, c, i * 2);
    if(r > c) update(l, r, x, c + 1, t, i * 2 + 1);
    pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
}
// 更新结点i左右子结点的区间和/懒惰标记值/updated[i]，最后重置懒惰标记值/updated[i]
private void pushDown(int s, int c, int t, int i){ 
    tree[i * 2] = (c - s + 1) * lazy[i]; // 更新其左子结点的区间和
    lazy[i * 2] = lazy[i]; // 传递懒标记(覆盖式标记)
    updated[i * 2] = true;
    tree[i * 2 + 1] = (t - c) * lazy[i];
    lazy[i * 2 + 1] = lazy[i];
    updated[i * 2 + 1] = true;
    lazy[i] = 0; // 重置当前结点懒惰标记值（覆盖式标记置0）
    updated[i] = false; // 重置当前结点updated[i]为false
}

类的实现代码

增量式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
/**
 * 静态线段树 (带懒标记，增量式区间修改)
 * 支持：单点修改 / 单点查询 / 区间求和 / 增量式区间修改
 */
class SegmentTreeAdd{
    int[] nums, tree, lazy;
    int n;
    public SegmentTreeAdd(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n];
        this.lazy = new int[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public void add(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        add(l, r, x, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] = x; // 覆盖更新
            return;
        }
        int c = s + (t - s) / 2;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, i * 2);
        else update(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) return query(idx, s, c, i * 2);
        else return query(idx, c + 1, t, i * 2 + 1);
    }
    // 区间修改: 增量式 [l,r] 区间所有元素加上x
    private void add(int l, int r, int x, int s, int t, int i){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            tree[i] += (t - s + 1) * x; // 结点i的区间和加上t-s+1个x
            if(s != t) lazy[i] += x; // 结点i不是叶子结点，懒标记值加上x
            return;
        }
        int c = s + (t - s) / 2;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) add(l, r, x, s, c, i * 2);
        if(r > c) add(l, r, x, c + 1, t, i * 2 + 1);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i]; // 当前结点代表的区间在所求区间之内
        int c = s + (t - s) / 2, sum = 0;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, i * 2);
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i]; // 叶子结点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(lazy[i] != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, i * 2);
        if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(lazy[i] != 0) pushDown(s, c, t, i);
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前结点区间起点下标，t: terminal,nums当前结点区间末尾下标
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUp(i);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // pushup: 更新 tree[i]
    private void pushUp(int i){
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记
    private void pushDown(int s, int c, int t, int i){
        tree[i * 2] += (c - s + 1) * lazy[i]; // 更新其左子结点的区间和
        lazy[i * 2] += lazy[i]; // 传递懒标记(增量标记)
        tree[i * 2 + 1] += (t - c) * lazy[i];
        lazy[i * 2 + 1] += lazy[i];
        lazy[i] = 0; // 重置当前结点懒惰标记值（增量标记置0）
    }
}

覆盖式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
/**
 * 静态线段树 (带懒标记，覆盖式区间修改为)
 * 支持：单点修改 / 单点查询 / 区间求和 / 覆盖式区间修改
 */
class SegmentTreeUpdate{
    int[] nums, tree, lazy;
    boolean[] updated;
    int n;
    public SegmentTreeUpdate(int[] nums){
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[4 * n];
        this.lazy = new int[4 * n];
        this.updated = new boolean[4 * n];
        build(0, n - 1, 1);
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public void update(int l, int r, int x){ // 区间修改(驱动): 覆盖式 [l,r] 区间所有元素改为x
        update(l, r, x, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] += x; // 增量更新
            return;
        }
        int c = s + (t - s) / 2;
        if(updated[i]) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, i * 2);
        else add(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i] = x; // 覆盖更新
            return;
        }
        int c = s + (t - s) / 2;
        if(updated[i]) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, i * 2);
        else update(idx, x, c + 1, t, i * 2 + 1);
        pushUp(i);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2;
        if(updated[i]) pushDown(s, c, t, i); // 当前结点懒惰标记不为0
        if(idx <= c) return query(idx, s, c, i * 2);
        else return query(idx, c + 1, t, i * 2 + 1);
    }
    // 区间修改: 覆盖式 [l,r] 区间所有元素改为x
    private void update(int l, int r, int x, int s, int t, int i){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            tree[i] = (t - s + 1) * x; // 结点i的区间和等于t-s+1个x
            if(s != t) { // 结点i不是叶子结点
                lazy[i] = x; // 更新懒标记
                updated[i] = true; // 更新updated
            }
            return;
        }
        int c = s + (t - s) / 2;
        if(updated[i]) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) update(l, r, x, s, c, i * 2);
        if(r > c) update(l, r, x, c + 1, t, i * 2 + 1);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i]; // 当前结点代表的区间在所要求的区间之内
        int c = s + (t - s) / 2, sum = 0;
        if(updated[i]) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, i * 2);
        if(r > c) sum += sum(l, r, c + 1, t, i * 2 + 1);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i]; // 叶子结点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(updated[i]) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, i * 2);
        if(r > c) rmin = min(l, r, c + 1, t, i * 2 + 1);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i];
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(updated[i]) pushDown(s, c, t, i);
        if(l <= c) lmax = max(l, r, s, c, i * 2);
        if(r > c) rmax = max(l, r, c + 1, t, i * 2 + 1);
        return Math.max(lmax, rmax);
    }
    // 构建线段树(tree数组)
    private void build(int s, int t, int i){
        if(s == t) { // s: start,nums当前结点区间起点下标，t: terminal,nums当前结点区间末尾下标
            tree[i] = nums[s];
            return;
        }
        int c = s + (t - s) / 2;
        build(s, c, i * 2);
        build(c + 1, t, i * 2 + 1);
        pushUp(i);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // pushup: 更新 tree[i]
    private void pushUp(int i){
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记和updated
    private void pushDown(int s, int c, int t, int i){
        tree[i * 2] = (c - s + 1) * lazy[i]; // 更新其左子结点的区间和
        lazy[i * 2] = lazy[i]; // 传递懒标记(覆盖式标记)
        updated[i * 2] = true;
        tree[i * 2 + 1] = (t - c) * lazy[i];
        lazy[i * 2 + 1] = lazy[i];
        updated[i * 2 + 1] = true;
        lazy[i] = 0; // 重置当前结点懒惰标记值
        updated[i] = false; // 重置当前结点updated[i]为false
    }
}

小结

学会了带懒惰标记的线段树后，对于「区间问题」，我们终于掌握了一个比「树状数组」更强大的工具。对于大小为 nn 的序列 numsnums ，带懒惰标记的线段树，同时以 O(logn)O(logn) 时间复杂度支持 「单点修改」、「单点查询」、「区间修改」和「区间查询」 。其中，「区间修改」支持增量式或覆盖式，「区间查询」除了能求区间和，也可以求区间最值，但是要注意 tree[]tree[] 定义为「区间和」或「区间最值」时，求区间最值的方法时间复杂度不同，这一点我们在「区间最值查询」小节中已作讨论。

实际上线段树经过一些调整，能够实现更多的区间运算。


离散化

当我们满怀信心带着已掌握的工具试图求解线段树题目时，我们马上会遇到一个难题 ── 空间爆炸！仍以 699. 掉落的方块 为例，题意不难理解，实际上就是要实现「覆盖式区间修改」和「区间最大值查询」操作。根据题目的数据范围提示，求解区间从 1 到 最右边方块的右界 为止，这个值是 n=108+106n=10^8+10^6 。按照我们目前为止讲解的堆式线段树的做法，tree[]tree[] 的大小将达到 4∗n=4∗(108+106)4*n=4*(10^8+10^6) ，会 MLEMLE 。

解决该问题的办法我们实际上已在「树状数组」中介绍过，那就是在不影响求解的情况下，先将求解区间离散化。以 699 题为例，方块 [l,l+h][l,l+h] 掉落时，我们首先在 [l,l+h−1][l,l+h-1] 区间内查询最大高度 heightheight ，然后将此区间修改为 h+heighth + height 。我们发现，只要保证所有方块的左右界的前后关系 (大小关系) 保持不变， 则像下图那样将所有方块的左右界一起离散化后，原问题的解不变。具体求解过程和代码可参考 题解 。

image.png

离散化主要分为紧离散和松离散，它们都基于排序，二者的区别已在「树状数组」中讲解过。


紧离散

借助 setset 去重，使得离散化后的有效数字更少，取值范围更小。

1
2
3
4
5
6
7
8
9
10
11
// 紧离散
private Map<Integer, Integer> discrete(int[] nums){ 
    Map<Integer, Integer> map = new HashMap<>();
    Set<Integer> set = new HashSet<>();
    for(int num : nums) set.add(num);
    List<Integer> list = new ArrayList<>(set);
    Collections.sort(list);
    int idx = 0;
    for(int num : list) map.put(num, ++idx);
    return map;
}

松离散

不借助 setset 去重，离散化后的有效数字更多 (存在相同的数字)，取值范围更大。

1
2
3
4
5
6
7
8
9
10
// 松离散
private void discrete(int[] nums){ 
    int n = nums.length;
    int[] tmp = new int[n];
    System.arraycopy(nums, 0, tmp, 0, n);
    Arrays.sort(tmp);
    for (int i = 0; i < n; ++i) {
        nums[i] = Arrays.binarySearch(tmp, nums[i]) + 1;
    }
}

举例而言，对于 nums={2,4,4,6}nums=\{2,4,4,6\} ，松离散得到 nums={1,2,2,4}nums=\{1,2,2,4\}，离散化后的 numsnums 大小与原来相同；紧离散得到 map={(2,1),(4,2),(6,3)}map=\{(2,1),(4,2),(6,3)\} ， keykey 为 numsnums 中的元素，对应的 valuevalue 为其离散化值，valuevalue 一定是从 1 开始的没有重复的连续正整数。

两种方式离散化后虽然有效数字不同，取值范围也不同，但通常都是有效的。松离散无需哈希计算，通常速度更快，但有的题目可能更适合返回 mapmap 的紧离散，可根据实际情况选取合适的离散化方式。


动态开点

现在，有了「离散化」这一工具，我们重新出发。在用「离散化」锤掉 699 题之后，继续尝试解决 715. Range 模块 一题。按如下理解题意，不难看出这也是一道非常典型的线段树题目。可用支持覆盖式「区间修改」和「区间查询 (求和)」的线段树实现。

  • addRangeaddRange 方法即覆盖式「区间修改」，我们可以视作将区间 [left,right−1][left,right-1] 的每个元素修改为 1。
  • queryRangequeryRange 方法即「区间查询」，对区间 [left,right−1][left,right-1] 求和，若 sum=right−leftsum = right-left 返回 truetrue ，否则返回 falsefalse 。
  • removeRangeremoveRange 方法也是覆盖式「区间修改」，将区间 [left,right−1][left,right-1] 的每个元素修改为 0。

根据题目给出的取值范围，我们看到「区间」范围为 [1,109][1,10^9] ，直接用堆式线段树则 tree[]tree[] 数组大小达到 4∗1094*10^9 ，会 MLEMLE 。当我们打算通过「离散化」来缩小区间时，发现本题是 强制在线 的，也就是并未提前告诉我们所有涉及询问和修改的区间范围，因此无法离散化。

※ log(4∗109)>31，231=2Gbitlog(4*10^9) > 31 ，2^{31} = 2Gbit ，因此要创建大小为 4∗1094*10^9 的数组，就需要超过 2Gb2Gb 的空间。

现在请看向本小节的标题 —— 「动态开点」 ，如果你此前有瞥过一些线段树的文章，你应该没少看到过这个词。总之你大概知道既然不能在程序开始时就完成初始「线段树」的构建的话，那就在区间查询或区间修改时，根据届时传入的区间信息来「动态地」创建结点，那么如何做到呢？

为了引出如何动态创建结点，我们先回顾「堆式线段树」的操作。每个结点代表一个确定的区间，当我们需要查询或修改区间 [l,r][l,r] 时，就要找到代表 [l,r][l,r] 的若干结点，操作它们的 tree[i]tree[i] 值和相应的 lazy/updatedlazy/updated (如果有的话)。我们需要知道搜索过程中结点代表的区间范围 [s,t][s,t] ，通过与 [l,r][l,r] 的比较来确定是否是目标区间，同时也要知道这个结点的下标 ii 使得我们能够操作 tree[i]tree[i] ，因此 s,t,is,t,i 三者是绑定的。总之，查找目标区间的关键是:

方法执行过程中保证结点值 (指 tree[i]tree[i]，一般为区间和 ) 和该结点代表的区间 [s,t][s,t] 是同时获知的。

堆式线段树通过 i,2∗i,2∗i+1i, 2*i, 2*i+1 下标关系实现了这一点。但只要我们能实现以上描述，线段树不必是「堆式」的。

一个直接的想法是不再由 int[] tree 来存储结点值信息，而是以 Node[] tree 来维护结点信息，NodeNode 可以作为线段树类中的嵌套类，它持有结点的值信息 valval (一般为区间和) ，此外还持有它的左右孩子的下标 lIdx,rIdxlIdx, rIdx ，这样当我们要递归进入左右孩子结点 (左右子区间) 时，就可以直接从当前结点读取下标，将 tree[tree[i].lIdx]tree[tree[i].lIdx] 或 tree[tree[i].rIdx]tree[tree[i].rIdx] 传入方法中，实现结点信息 (tree[tree[i].lIdx].valtree[tree[i].lIdx].val 或 tree[tree[i].rIdx].valtree[tree[i].rIdx].val) 和 [s,t][s,t] 的同时获知。

到这里，我们实际上已经给出了「动态开点线段树」的第一种实现方式 —— 结点数组法。


结点数组法

我们直接给出如下包含了构造器和区间修改 (增量式) 的代码，结合后图分析 「结点数组法动态线段树」 是如何「动态开点」的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class DynamicSegmentTreeArrayAdd{ 
    private class Node{
        int lIdx, rIdx, lazy, val;
    }
    Node[] tree;
    int n, count;
    public DynamicSegmentTreeArrayAdd(int n, int m){
        this.n = n;
        this.count = 1;
        this.tree = new Node[m];
    }
    public void add(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        add(l, r, x, 0, n - 1, 1);
    }    
    // 区间修改: 增量式 [l,r] 区间所有元素加上x
    private void add(int l, int r, int x, int s, int t, int i){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            tree[i].val += (t - s + 1) * x; // 结点i的区间和加上t-s+1个x
            if(s != t) tree[i].lazy += x; // 结点i不是叶子结点，懒标记值加上x
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) add(l, r, x, s, c, tree[i].lIdx);
        if(r > c) add(l, r, x, c + 1, t, tree[i].rIdx);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 动态开点
    private void addNode(int i){
        if(tree[i] == null) tree[i] = new Node(); // 当前结点未建，创建之
        if(tree[i].lIdx == 0) { // 若 tree[i] 结点无左孩子，添加之
            tree[i].lIdx = ++count; // 赋予结点标号
            tree[tree[i].lIdx] = new Node(); // 开辟实例
        }
        if(tree[i].rIdx == 0) { // 若 tree[i] 结点无右孩子，添加之
            tree[i].rIdx = ++count;
            tree[tree[i].rIdx] = new Node();
        }
    }
}

首先看构造器。nn 是输入区间的大小，它的范围是 [0,n−1][0,n-1] 。 整个区间的范围是必须知道的 ，因为我们要从输入区间开始不断划分左右区间，因此要传入 nn 。 mm 是 treetree 的大小，因为在这个实现中 tree[]tree[] 是 NodeNode 数组，初始化它必须要给出数组大小。在堆式线段树中，这个大小是 4∗n4*n ，但前面已经说过 nn 特别大，且由于「强制在线」而无法离散化，因此这个大小需要 「估计」 ，估计方法后述。

接着看区间修改的驱动方法和具体的区间修改方法，它们与我们前面给出的堆式线段树的写法几乎相同，区别只在于多了一行 addNode(i) 。 addadd 运行到此处时，之后会划分当前区间为左右子区间，然后带着区间信息和左右子结点的信息递归调用 addadd (递进到左右子结点中) 。但是我们 尚未创建左右子结点，甚至当前结点也可能尚未创建 ，因此必须执行 addNode(i) ，根据方法中的判断结果来决定是否要创建当前结点 tree[i]tree[i] 、左子结点 tree[tree[i].lIdx]tree[tree[i].lIdx] 或右子结点 tree[tree[i].rIdx]tree[tree[i].rIdx] 。我们注意到结点编号是从 1 开始递增的，因此判断是否存在子结点时， 可以不必像判断当前结点是否存在那样执行 tree[tree[i].lIdx] == null 而是通过 tree[i].lIdx == 0 来判断即可。

同样地，对于其他查询或修改方法，与堆式线段树的实现的区别都只是是在方法中多了 addNode(i) 这一行「开点」语句，如此就实现了 只在查询或修改时按需动态地创建结点 这一目标。 完整的类实现我们放在稍后的「类的实现代码」中。如下 ①~⑨ 是在区间为 [0,14][0,14] 的输入序列上修改区间 [1,3][1,3] 时依次动态创建的结点，注意结点标号是从 1 开始递增的。

image.png


预估结点数

tree[]tree[] 的大小 mm 需要预估。从上图过程中我们看到，每次查询或修改操作的「开点」次数与树高有关，我们知道树高 hh 与叶子结点数 nn (即我们必须知道的区间大小) 的关系，因此只要能够提前知道操作总次数 (查询和修改) ，并假设查询或修改的区间 不太大，我们就能估计经过所有操作后创建的总的结点数，即线段树的大小 mm。 如下：

  1. 整棵线段树的结点数不会超过 4∗n4*n 。
  2. 每次查询从根结点往下，在假设查询或修改的区间 只有一个值 ，则每次操作从根结点到表示该值的叶子结点的路径上，每一层只会经过一个区间，开两个点。于是开点次数为树高 h=⌈log2(4∗n)⌉−1=log2(4∗n)h = \lceil log_{2}(4*n) \rceil -1=log_{2}(4*n) (根结点高 0)，每次开两个点，一次查询最多新建 2∗h2*h 个结点。但平均而言操作的区间当然不会只有一个值，因此这里我们要适当放大倍数，根据经验可放大到 6∗h6*h 。
  3. 假设有 kk 次操作，则有估计 m=6∗k∗log2(4∗n)m=6*k*log_{2}(4*n) ，省略 6∗k∗26*k*2 后得到 m=6∗k∗lognm = 6*k*logn 。

现在，在参考「类的实现代码」中「结点数组法」版本的代码以及 题解 的基础上，应当很容易写出「结点数组法动态线段树」解决 715. Range 模块 。

应用结点数组法动态线段树解决 715题 时，我们会感到 mm 的预估相对麻烦 ，估计偏小时还可能出现数组越界的错误。让我们考虑更严格的情况。假设操作次数也未知，那么我们将无法估计 mm ，也就无法很好地使用结点上数组法来实现动态线段树，除非像 ArrayListArrayList 内部动态扩展数组那样，当空间不够时再将当前 tree[]tree[] 拷贝到新申请的更大的 NodeNode 数组中，但如此一来单次查询或修改的时间复杂度就不保证是 O(logn)O(logn) 了。

避免数组大小预估的思考引出下面的 「结点指针 (引用)」法动态线段树」 。


结点指针 (引用) 法

避免数组大小预估的办法很简单。我们不再通过数组来保存结点信息，而是在 NodeNode 中持有同样是 NodeNode 类型的左子结点 lChildlChild 和右子结点 rChildrChild 。如此一来，在处理到代表区间 [l,r][l,r] 的当前结点 curcur 时，我们总是能够将左右子区间分别与 cur.lChildcur.lChild 或 cur.rChildcur.rChild 「绑定」起来。其实只要读者熟悉二叉树的一些操作，该方法反而比结点数组法要更容易想到。

结点指针法实现的动态线段树是简单的。我们直接给出如下包含了构造器和区间修改 (增量式) 的代码，对比「结点数组」法的代码，主要区别为：

  • 指针法的查询或修改方法，直接传入当前结点 Node cur 。
  • 指针法的线段树类维护根结点 rootroot 。
  • 动态开点方法 addNodeaddNode 不同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class DynamicSegmentTreePointerAdd{
    private class Node{
        int lazy, val;
        Node lChild, rChild;
    }
    int n;
    Node root;
    public DynamicSegmentTreePointerAdd(int n){
        this.n = n;
        this.root = new Node();
    }
    public void add(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        add(l, r, x, 0, n - 1, root);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, Node cur){ 
        if(s == t) {
            cur.val += x; // 增量更新
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 当前结点懒惰标记不为0，推送标记
        if(idx <= c) add(idx, x, s, c, cur.lChild);
        else add(idx, x, c + 1, t, cur.rChild);
        pushUp(cur); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 动态开点
    private void addNode(Node node){ 
        if(node.lChild == null) node.lChild = new Node();
        if(node.rChild == null) node.rChild = new Node();
    }
}

完整实现请参考「类的实现代码」。

从前面一步步看到这里，我们明显感到动态开点的线段树并不复杂，相比静态线段树，实现上的区别不过是引入了一个 addNodeaddNode 方法，并在查询和修改方法的适当位置调用该方法动态地创建结点而已。

现在，在参考「类的实现代码」中「结点指针 (引用) 法」版本的代码以及 题解 的基础上，应当很容易写出「结点指针 (引用) 法动态线段树」解决 715. Range 模块 。


类的实现代码

结点数组法
增量式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
/**
 * 动态开点线段树数组版 (带懒标记，覆盖式区间修改)
 * 支持：单点修改 / 单点查询 / 区间求和 / 覆盖式区间修改
 */
class DynamicSegmentTreeArrayAdd{
    private class Node{
        int lIdx, rIdx, lazy, val;
    }
    Node[] tree;
    int n, count;
    public DynamicSegmentTreeArrayAdd(int n, int m){
        this.n = n;
        this.count = 1;
        this.tree = new Node[m];
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public void add(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        add(l, r, x, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i].val += x; // 增量更新
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, tree[i].lIdx);
        else add(idx, x, c + 1, t, tree[i].rIdx);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i].val = x; // 覆盖更新
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, tree[i].lIdx);
        else update(idx, x, c + 1, t, tree[i].rIdx);
        pushUp(i);  // 后序动作，自底向上更新结点值
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i].val;
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) return query(idx, s, c, tree[i].lIdx);
        else return query(idx, c + 1, t, tree[i].rIdx);
    }
    // 区间修改: 增量式 [l,r] 区间所有元素加上x
    private void add(int l, int r, int x, int s, int t, int i){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            tree[i].val += (t - s + 1) * x; // 结点i的区间和加上t-s+1个x
            if(s != t) tree[i].lazy += x; // 结点i不是叶子结点，懒标记值加上x
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) add(l, r, x, s, c, tree[i].lIdx);
        if(r > c) add(l, r, x, c + 1, t, tree[i].rIdx);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i].val; // 当前结点代表的区间在所求区间之内
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, sum = 0;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, tree[i].lIdx);
        if(r > c) sum += sum(l, r, c + 1, t, tree[i].rIdx);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i].val; // 叶子结点
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(tree[i].lazy != 0) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, tree[i].lIdx);
        if(r > c) rmin = min(l, r, c + 1, t, tree[i].rIdx);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i].val;
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(tree[i].lazy != 0) pushDown(s, c, t, i);
        if(l <= c) lmax = max(l, r, s, c, tree[i].lIdx);
        if(r > c) rmax = max(l, r, c + 1, t, tree[i].rIdx);
        return Math.max(lmax, rmax);
    }
    // pushup: 更新 cur.val
    private void pushUp(int i){
        Node cur = tree[i], lChild = tree[cur.lIdx], rChild = tree[cur.rIdx];
        cur.val = lChild.val + rChild.val;
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记
    private void pushDown(int s, int c, int t, int i){
        Node cur = tree[i], lChild = tree[cur.lIdx], rChild = tree[cur.rIdx];
        lChild.val += (c - s + 1) * cur.lazy; // 更新其左子结点的区间和
        lChild.lazy += cur.lazy; // 传递懒标记
        rChild.val += (t - c) * cur.lazy;
        rChild.lazy += cur.lazy;
        cur.lazy = 0;
    }
    // 动态开点
    private void addNode(int i){
        if(tree[i] == null) tree[i] = new Node(); // 当前结点未建，创建之
        if(tree[i].lIdx == 0) { // 若 tree[i] 结点无左孩子，添加之
            tree[i].lIdx = ++count; // 赋予结点标号
            tree[tree[i].lIdx] = new Node(); // 开辟实例
        }
        if(tree[i].rIdx == 0) { // 若 tree[i] 结点无右孩子，添加之
            tree[i].rIdx = ++count;
            tree[tree[i].rIdx] = new Node();
        }
    }
}

覆盖式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
/**
 * 动态开点线段树数组版 (带懒标记，覆盖式区间修改为)
 * 支持：单点修改 / 单点查询 / 区间求和 / 覆盖式区间修改
 */
class DynamicSegmentTreeArrayUpdate{
    private class Node{
        int lIdx, rIdx, lazy, val;
        boolean updated;
    }
    Node[] tree;
    int n, count;
    public DynamicSegmentTreeArrayUpdate(int n, int m){
        this.n = n;
        this.count = 1;
        this.tree = new Node[m];
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, 1);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, 1);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, 1);
    }
    public void update(int l, int r, int x){ // 区间修改(驱动): 覆盖式 [l,r] 区间所有元素改为x
        update(l, r, x, 0, n - 1, 1);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, 1);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, 1);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, 1);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i].val += x; // 增量更新
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, tree[i].lIdx);
        else add(idx, x, c + 1, t, tree[i].rIdx);
        pushUp(i); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, int i){
        if(s == t) {
            tree[i].val = x; // 覆盖更新
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, tree[i].lIdx);
        else update(idx, x, c + 1, t, tree[i].rIdx);
        pushUp(i);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点查询 (具体): 查询 nums[i]，尾递归
    private int query(int idx, int s, int t, int i){
        if(s == t) return tree[i].val;
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(idx <= c) return query(idx, s, c, tree[i].lIdx);
        else return query(idx, c + 1, t, tree[i].rIdx);
    }
    // 区间修改: 覆盖式 [l,r] 区间所有元素改为x
    private void update(int l, int r, int x, int s, int t, int i){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            tree[i].val = (t - s + 1) * x; // 结点i的区间和等于t-s+1个x
            if(s != t) {
                tree[i].lazy = x; // 更新懒标记
                tree[i].updated = true; // 更新updated
            }
            return;
        }
        addNode(i); // 动态开点
        int c = s + (t - s) / 2;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) update(l, r, x, s, c, tree[i].lIdx);
        if(r > c) update(l, r, x, c + 1, t, tree[i].rIdx);
        pushUp(i); // 后序动作，自底向上更新结点值
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, int i){
        if(l <= s && t <= r) return tree[i].val; // 当前结点代表的区间在所求区间之内
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, sum = 0;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, tree[i].lIdx);
        if(r > c) sum += sum(l, r, c + 1, t, tree[i].rIdx);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, int i){
        if(s == t) return tree[i].val; // 叶子结点
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, tree[i].lIdx);
        if(r > c) rmin = min(l, r, c + 1, t, tree[i].rIdx);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, int i){
        if(s == t) return tree[i].val;
        addNode(i); // 动态开点
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(tree[i].updated) pushDown(s, c, t, i); // 是否推送标记
        if(l <= c) lmax = max(l, r, s, c, tree[i].lIdx);
        if(r > c) rmax = max(l, r, c + 1, t, tree[i].rIdx);
        return Math.max(lmax, rmax);
    }
    // 更新 cur.val
    private void pushUp(int i){
        Node cur = tree[i], lChild = tree[cur.lIdx], rChild = tree[cur.rIdx];
        cur.val = lChild.val + rChild.val;
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记和updated
    private void pushDown(int s, int c, int t, int i){
        Node cur = tree[i], lChild = tree[cur.lIdx], rChild = tree[cur.rIdx];
        lChild.val = (c - s + 1) * cur.lazy; // 更新左子结点的区间和
        lChild.lazy = cur.lazy; // 传递懒标记(增量标记)到左子结点中
        lChild.updated = true; // 更新左子结点updated
        rChild.val = (t - c) * cur.lazy;
        rChild.lazy = cur.lazy;
        rChild.updated = true;
        cur.lazy = 0; // 重置当前结点懒惰标记值
        cur.updated = false; // 更新updated
    }
    // 动态开点
    private void addNode(int i){
        if(tree[i] == null) tree[i] = new Node();
        if(tree[i].lIdx == 0) { // 若 tree[i] 结点无左孩子，添加之
            tree[i].lIdx = ++count; // 赋予结点标号
            tree[tree[i].lIdx] = new Node(); // 开辟实例
        }
        if(tree[i].rIdx == 0) { // 若 tree[i] 结点无右孩子，添加之
            tree[i].rIdx = ++count;
            tree[tree[i].rIdx] = new Node();
        }
    }
}

结点指针 (引用) 法
增量式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
/**
 * 动态开点线段树指针版 (带懒标记，增量式区间修改)
 * 支持：单点修改 / 单点查询 / 区间求和 / 增量式区间修改
 */
class DynamicSegmentTreePointerAdd{
    private class Node{
        int lazy, val;
        Node lChild, rChild;
    }
    int n;
    Node root;
    public DynamicSegmentTreePointerAdd(int n){
        this.n = n;
        this.root = new Node();
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, root);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, root);
    }
    public int query(int i){ // 单点查询 (驱动): 查询 nums[i]
        return query(i, 0, n - 1, root);
    }
    public void add(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        add(l, r, x, 0, n - 1, root);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, root);
    }
    public int min(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, root);
    }
    public int max(int l, int r){ // 区间查询 (驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, root);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, Node cur){
        if(s == t) {
            cur.val += x; // 增量更新
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, cur.lChild);
        else add(idx, x, c + 1, t, cur.rChild);
        pushUp(cur); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, Node cur){
        if(s == t) {
            cur.val = x; // 覆盖更新
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, cur.lChild);
        else update(idx, x, c + 1, t, cur.rChild);
        pushUp(cur);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点查询: 查询 nums[i]，尾递归
    private int query(int i, int s, int t, Node cur){
        if(s == t) return cur.val;
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(i <= c) return query(i, s, c, cur.lChild);
        else return query(i, c + 1, t, cur.rChild);
    }
    // 区间修改: 增量式 [l,r] 区间所有元素加上x
    private void add(int l, int r, int x, int s, int t, Node cur){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            cur.val += (t - s + 1) * x; // 结点i的区间和加上t-s+1个x
            if(s != t) cur.lazy += x; // 结点i不是叶子结点，懒标记值加上x
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) add(l, r, x, s, c, cur.lChild);
        if(r > c) add(l, r, x, c + 1, t, cur.rChild);
        pushUp(cur); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, Node cur){
        if(l <= s && t <= r) return cur.val; // 当前结点代表的区间在所求区间之内
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2, sum = 0;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, cur.lChild);
        if(r > c) sum += sum(l, r, c + 1, t, cur.rChild);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, Node cur){
        if(s == t) return cur.val; // 叶子结点
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(cur.lazy != 0) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, cur.lChild);
        if(r > c) rmin = min(l, r, c + 1, t, cur.rChild);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, Node cur){
        if(s == t) return cur.val;
        addNode(cur);
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(cur.lazy != 0) pushDown(s, c, t, cur);
        if(l <= c) lmax = max(l, r, s, c, cur.lChild);
        if(r > c) rmax = max(l, r, c + 1, t, cur.rChild);
        return Math.max(lmax, rmax);
    }
    // pushup: 更新 cur.val
    private void pushUp(Node cur){
        Node lChild = cur.lChild, rChild = cur.rChild;
        cur.val = lChild.val + rChild.val;
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记
    private void pushDown(int s, int c, int t, Node cur){
        Node lChild = cur.lChild, rChild = cur.rChild;
        lChild.val += (c - s + 1) * cur.lazy; // 更新其左子结点的区间和
        lChild.lazy += cur.lazy; // 传递懒标记
        rChild.val += (t - c) * cur.lazy;
        rChild.lazy += cur.lazy;
        cur.lazy = 0; // 重置当前结点懒惰标记值
    }
    // 动态开点
    private void addNode(Node node){
        if(node.lChild == null) node.lChild = new Node();
        if(node.rChild == null) node.rChild = new Node();
    }
}

覆盖式区间修改版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
/**
 * 动态开点线段树指针版 (带懒标记，覆盖式区间修改)
 * 支持：单点修改 / 单点查询 / 区间查询 / 覆盖式区间修改
 */
class DynamicSegmentTreePointerUpdate{
    private class Node{
        int lazy, val;
        boolean updated;
        Node lChild, rChild;
    }
    int n;
    Node root;
    public DynamicSegmentTreePointerUpdate(int n){
        this.n = n;
        this.root = new Node();
    }
    public void add(int i, int x){ // 单点修改(驱动): 增量式 nums[i] += x
        add(i, x, 0, n - 1, root);
    }
    public void update(int i, int x){ // 单点修改(驱动): 覆盖式 nums[i] = x
        update(i, x, 0, n - 1, root);
    }
    public int query(int i){ // 单点查询(驱动): 查询 nums[i]
        return query(i, 0, n - 1, root);
    }
    public void update(int l, int r, int x){ // 区间修改(驱动): 增量式 [l,r] 区间所有元素加上x
        update(l, r, x, 0, n - 1, root);
    }
    public int sum(int l, int r){ // 区间查询(驱动): nums[l]~nums[r]之和
        return sum(l, r, 0, n - 1, root);
    }
    public int min(int l, int r){ // 区间查询(驱动): 查询[l,r]中的最小值
        return min(l, r, 0, n - 1, root);
    }
    public int max(int l, int r){ // 区间查询(驱动): 查询[l,r]中的最大值
        return max(l, r, 0, n - 1, root);
    }
    // 单点修改: 增量式 令nums[idx] += x。修改叶子结点，无关标记。
    private void add(int idx, int x, int s, int t, Node cur){
        if(s == t) {
            cur.val += x; // 增量更新
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(idx <= c) add(idx, x, s, c, cur.lChild);
        else add(idx, x, c + 1, t, cur.rChild);
        pushUp(cur); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点修改: 覆盖式 令nums[idx] = x。修改叶子结点，无关标记。
    private void update(int idx, int x, int s, int t, Node cur){
        if(s == t) {
            cur.val = x; // 覆盖更新
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(idx <= c) update(idx, x, s, c, cur.lChild);
        else update(idx, x, c + 1, t, cur.rChild);
        pushUp(cur);  // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 单点查询: 查询 nums[i]，尾递归
    private int query(int i, int s, int t, Node cur){
        if(s == t) return cur.val;
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(i <= c) return query(i, s, c, cur.lChild);
        else return query(i, c + 1, t, cur.rChild);
    }
    // 区间修改: 覆盖式 [l,r] 区间所有元素改为x
    private void update(int l, int r, int x, int s, int t, Node cur){
        if(l <= s && t <= r){ // 当前结点代表的区间在所求区间之内
            cur.val = (t - s + 1) * x; // 结点i的区间和等于t-s+1个x
            if(s != t) { // 结点i不是叶子结点
                cur.lazy = x; // 更新懒标记
                cur.updated = true; // 更新updated
            }
            return;
        }
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) update(l, r, x, s, c, cur.lChild);
        if(r > c) update(l, r, x, c + 1, t, cur.rChild);
        pushUp(cur); // 后序动作，自底向上更新结点区间和 tree[i]
    }
    // 区间查询: 求 nums[l]~nums[r]之和
    private int sum(int l, int r, int s, int t, Node cur){
        if(l <= s && t <= r) return cur.val; // 当前结点代表的区间在所求区间之内
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2, sum = 0;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) sum += sum(l, r, s, c, cur.lChild);
        if(r > c) sum += sum(l, r, c + 1, t, cur.rChild);
        return sum;
    }
    // 区间查询: 查询[l,r]中的最小值
    private int min(int l, int r, int s, int t, Node cur){
        if(s == t) return cur.val; // 叶子结点
        addNode(cur); // 动态开点
        int c = s + (t - s) / 2, lmin = Integer.MAX_VALUE, rmin = Integer.MAX_VALUE;
        if(cur.updated) pushDown(s, c, t, cur); // 是否推送标记
        if(l <= c) lmin = min(l, r, s, c, cur.lChild);
        if(r > c) rmin = min(l, r, c + 1, t, cur.rChild);
        return Math.min(lmin, rmin);
    }
    // 区间查询: 查询[l,r]中的最大值
    private int max(int l, int r, int s, int t, Node cur){
        if(s == t) return cur.val;
        addNode(cur);
        int c = s + (t - s) / 2, lmax = Integer.MIN_VALUE, rmax = Integer.MIN_VALUE;
        if(cur.updated) pushDown(s, c, t, cur);
        if(l <= c) lmax = max(l, r, s, c, cur.lChild);
        if(r > c) rmax = max(l, r, c + 1, t, cur.rChild);
        return Math.max(lmax, rmax);
    }
    // pushup: 更新 cur.val
    private void pushUp(Node cur){
        Node lChild = cur.lChild, rChild = cur.rChild;
        cur.val = lChild.val + rChild.val;
    }
    // pushdown: 更新当前结点及其左右子结点的懒标记和updated
    private void pushDown(int s, int c, int t, Node cur){
        Node lChild = cur.lChild, rChild = cur.rChild;
        lChild.val = (c - s + 1) * cur.lazy; // 更新其左子结点的区间和
        lChild.lazy = cur.lazy; // 传递懒标记(增量标记)
        lChild.updated = true;
        rChild.val = (t - c) * cur.lazy;
        rChild.lazy = cur.lazy;
        rChild.updated = true;
        cur.lazy = 0; // 重置当前结点懒惰标记值（增量标记置0）
        cur.updated = false;
    }
    // 动态开点
    private void addNode(Node node){
        if(node.lChild == null) node.lChild = new Node();
        if(node.rChild == null) node.rChild = new Node();
    }
}

总结

本文从基本的静态线段树到动态线段树，介绍了如下内容。

  • 基本原理： 通过 「完全二叉树下标性质」 和 「分治算法」 来理解基本线段树的工作原理。
  • 基本 (静态) 线段树： 首先实现了支持「单点修改」和「区间查询」的基本线段树，可解决 307. 区域和检索 - 数组可修改 。
  • 懒惰标记： 引入 「懒惰标记」 和 「延迟修改」 的概念，用以实现 O(logn)O(logn) 时间复杂度的 「区间修改」。
  • 离散化： 当区间问题与区间元素的绝对位置无关而只与它们的相对位置有关时，可以采用 「离散化」 压缩区间范围，典型题目如 699. 掉落的方块 。具体的离散化方法包括 「紧离散」 和 「松离散」 。
  • 动态开点： 当区间问题具有「强制在线」的特点时，由于无法离散化，迫使我们思考能否实现 「动态开点」 (动态地创建结点) 的线段树。典型题目如 715. Range 模块 。

    • 数组法动态线段树： 若能提前估计树的大小，可用 「结点数组法」 实现动态开点线段树。给出结点数估计方法。

      • 结点数估计: 在已知操作次数上限的情况下可以预估结点数，以便于初始化「结点数组」。

    • 指针法动态线段树： 通过 「结点指针 (引用) 法」 实现的动态开点线段树，无需预估树的大小。

文中我们给出了如下十种线段树的完整的类代码。

线段树类 描述
1. SegmentTreeBasic1SegmentTreeBasic1 基本静态线段树，不带懒惰标记，只支持单点修改和区间查询，实时维护 numsnums
2. SegmentTreeBasic2SegmentTreeBasic2 基本静态线段树，不带懒惰标记，只支持单点修改和区间查询，不维护 numsnums
3. SegmentTreeAddSegmentTreeAdd 静态线段树，带懒惰标记，支持单点修改/单点查询/增量式区间修改/区间查询
4. SegmentTreeUpdateSegmentTreeUpdate 静态线段树，带懒惰标记，支持单点修改/单点查询/覆盖式区间修改/区间查询
5. DynamicSegmentTreeArrayAddDynamicSegmentTreeArrayAdd 结点数组法动态线段树，带懒惰标记，支持单点修改/单点查询/增量式区间修改/区间查询
6. DynamicSegmentTreeArrayUpdateDynamicSegmentTreeArrayUpdate 结点数组法动态线段树，带懒惰标记，支持单点修改/单点查询/覆盖式区间修改/区间查询
7. DynamicSegmentTreePointerAddDynamicSegmentTreePointerAdd 结点指针法动态线段树，带懒惰标记，支持单点修改/单点查询/增量式区间修改/区间查询
8. DynamicSegmentTreePointerUpdateDynamicSegmentTreePointerUpdate 结点指针法动态线段树，带懒惰标记，支持单点修改/单点查询/覆盖式区间修改/区间查询
9. SegmentTreeBasicRangeMaxSegmentTreeBasicRangeMax 区间最大值基本静态线段树，无懒标记，不维护 nums[i]nums[i]，支持单点修改/单点查询/区间查询
10. SegmentTreeBasicSegmentTreeBasic 扩展区间查询基本静态线段树，无懒标记，不维护 nums[i]nums[i]，支持单点修改/单点查询/区间查询

注意，1~8 的实现中，tree[]tree[] 记录的是「区间和」，9记录的「最大值」，10以三个线段树数组同时记录「区间和」、「区间最大值」以及「区间最小值」。总之，将 1~8 中的 tree[]tree[] 用于记录「区间最值」，经过我们在「区间最值查询」小节中的调整，即可得到相应的以 O(logn)O(logn) 时间复杂度实现区间最值查询的线段树版本。

线段树的应用是十分灵活而强大的，本文只讲解了作者所知的最基本的一些内容，更多的应用已然超出了作者的水平。好在这些内容已基本足够求解力扣上几乎所有线段树题目。

※ 推荐清华大学张昆玮写的一份 101 页的 ppt 材料 统计的力量 —— 线段树全接触 ，可作为线段树应用的总览材料。


实战应用

题目 难度 题解
307. 区域和检索 - 数组可修改 中等 题解
699. 掉落的方块 困难 题解
715. Range 模块 困难 题解
218. 天际线问题 困难 题解
729. 我的日程安排表 I 中等 题解
731. 我的日程安排表 II 中等 题解
732. 我的日程安排表 III 困难 题解
253. 会议室 II 中等 题解
2407. 最长递增子序列 II 困难 题解
==== 更多题目追加中 ====

文章更新日志

[2022-09-18]

  • 增加了少量内容，说明 tree[]tree[] 代表「区间和」和「区间最值」时，求最值的方法 (maxmax , minmin) 的时间复杂度的区别。即当 tree[]tree[] 代表「区间和」时，求最值的方法的时间复杂度为 O(n)O(n) ，代表「区间最值」时，为 O(logn)O(logn) 。

[2022-08-03]