并查集从入门到出门

今天，就由你来发明并查集

• 可在作者的 github仓库 中获取本文和其他文章的 markdown 源文件及相关代码。

• 欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题，我将长期维护所有文章。

• 所有文章均用 Typora 完成写作，可使用 Typora 打开文章 md 文件，以获得最佳阅读体验。

⚠️ ⚠️ ⚠️ 本文较长，正文一万两千字 (不含题解) ，尝试展现如何从零开始发明并查集。

❗️ 【NEW】 ❗️

• 9-15: 红黑树从入门到看开

---

$keywords$ :

从零发明并查集 / 连通分量 / 查询与合并 / 按大小求并 / 按秩(高度)求并 / 路径压缩 / 负数技巧 / 反阿克曼函数

前几天 (20220509) 在讨论区发了篇文章 二分查找从入门到入睡 ，得到了蛮不错的反馈，这让我感觉到基础知识的总结和分享很有价值。从前一篇文章的点赞和一些评论中我还发现，虽然我们在力扣上总能看到一些知名 ID 的题解题评，但像我这样的小白用户才是大多数 ，因此我想尝试多分享一些主要面向小白的，我用心总结过的（也许是微不足道的）心得，于是有了这篇文章。

并查集以简单高效著称，理解起来并没有太大的难度，但如果只是 「输入式」 地学习，初学时总会觉得不够透彻，尤其是 「路径压缩」 ，以及 「秩」 的准确内涵。就好比你知道怎么写 $Dijkstra$ ，但你没有推导过一遍 该算法的正确性 ，你做起题来就总是不踏实。所以本文尝试以 「启发式」 的方式讲解，让初学者真正地从思考一个具体的问题开始，从无到有逐步创造一种数据结构解决之（当然并不是真的从零开始，你得知道链表、树、递归等基础知识）。原本你跟着一般教材，比如我手边的 Weiss 那本 数据结构与算法分析：Java语言描述 ，可能需要消化个一两天才能对并查集有掌控感，但我希望通过这篇文章把这个时间压缩到一两个小时之内（毕竟是你在全程发明并查集😄）。对于已经熟悉并查集，甚至是用并查集解决过不少问题的人，这篇文章可能也有一些看点。比如对于如下问题，如果你对自己的答案还有些犹疑的话，可以看看本文。

问题1: 为什么带路径压缩的并查集中基于高度的求并称作「按秩求并」而非「按高度求并」？可否给出严谨的说明？
问题2: 求并时比较大小或比较秩，总是通过两棵树的根的大小或秩比较，而且一次只比较两个根，随着合并的进行，根逐渐变少，大小数组或秩数组的大部分空间似乎没用到，你能优化这部分空间吗？

正文部分将从基本概念入手，呈现并查集的基本样貌，包括其适用的 问题特征 ，「查询」 和 「合并」 是怎么想到的，如何从「简单查询」和「简单求并」得到的基本并查集中看到优化方向，并实现一个优化后的查询，即 「带路径压缩的查询」 ，以及两个优化后的求并，即 「按大小求并」 和 「按秩 (高度) 求并」 。我还会准确地指出 「秩」的内涵 以回答上述「问题1」，并在文章末尾介绍一种 无需大小或秩数组空间的技巧 以回答上述「问题2」。最后会在「实战应用」中给出十几道题目的并查集解法，以便读者自查。

本文标题 意在表达作者的一种希望，即期待对并查集不太熟悉的你，在看完本文后能够 完全掌握 这一数据结构，且能够快速做完相关题目，出门 享受这个暮春（写于2022年暮春）。本文曾发布在个人知乎专栏中，也授权一位朋友发表在他自己的公众号上过。但我从读者的角度，以所谓 「独立发明」并查集 的视角出发，用一种全新的「冷幽默」写作风格（自封的），几乎重写了一遍。

为了说得更透彻，文章依旧是话痨风。文中若有疏漏之处，还希望大家不吝赐教，你所指出的文章中的任何错误我都会及时更正。下面我们开始发明并查集的旅程。

---

yuki的其他文章如下，欢迎阅读指正！

如下所有文章同时也在我的 github 仓库 中维护。

文章	[发布时间] 字数/览/藏/赞 (~2022-10-20)
十大排序从入门到入赘 🔥🔥🔥	[20220516] 2.5万字/64.8k览/3.7k藏/937赞
二分查找从入门到入睡 🔥🔥🔥	[20220509] 2.3万字/38.4k览/2.1k藏/503赞
并查集从入门到出门 🔥🔥	[20220514] 1.2万字/17.9k览/1.0k藏/321赞
图论算法从入门到放下 🔥🔥	[20220617] 5.6万字/19.9k览/1.3k藏/365赞
树ADT系列 (预计13篇)	系列文章，连载中
3. 二叉查找树	[20220801] 5千字
4. AVL树	[20220817] 5千字
5. splay树	[20220817] 5千字
6. 红黑树从入门到看开 🔥🤯🤯🤯	[20220915] 3万字/5.3k览/269藏/72赞
10. 树状数组从入门到下车 🔥🤯	[20220722] 1.4万字/5.8k览/196藏/72赞
11. 线段树从入门到急停 🔥🤯	[20220726] 2.5万字/8.7k览/481藏/138赞
图论相关证明系列	系列文章
1. Dijkstra正确性证明 🤯	[20220531]
2. Prim正确性证明 🤯	[20220919]
3. Bellman-Ford及SPFA正确性证明	[20220602]
4. Floyd正确性证明	[20220602]
5. 最大流最小割定理证明 🤯🤯	[20220719]
6. Edmonds-Karp复杂度证明 🤯🤯	[20220515]
7. Dinic复杂度证明 🤯🤯	[20220531]

---

[2022-07-31]

• 更正了「应用负数技巧」的并查集类的「按秩求并」方法的一处逻辑错误。该错误由 @you-lan-r4 (幽蓝) 发现并指出，感谢 🙏 。
• 修改了若干词句。

---

[TOC]

---

基本概念

我们以一个直观的问题引入并查集 (不相交集) 的概念。

※ 并查集: Union-Find Set ，不相交集: Disjoint Set。

亲戚问题： 有一群人，他们属于不同家族，同一个家族里的人互为亲戚，不同家族的人不是亲戚。已知每个人都知道自己与其他人是否有亲戚关系，求问有几个家族。

亲戚问题代表着一大类能用并查集解决的所谓确定「连通分量」的问题，可以将上述问题图示化如下，不同颜色的集合代表不同家族，集合内的人 (元素) 互为亲戚。从图论的角度来说，同一个集合内的元素是相互「连通」的，那么一个集合就是一个「连通分量」。用集合的语言来说，问题涉及的元素可划归到互相 没有交集 的集合，因此也称这样的结构为 「不相交集」 。

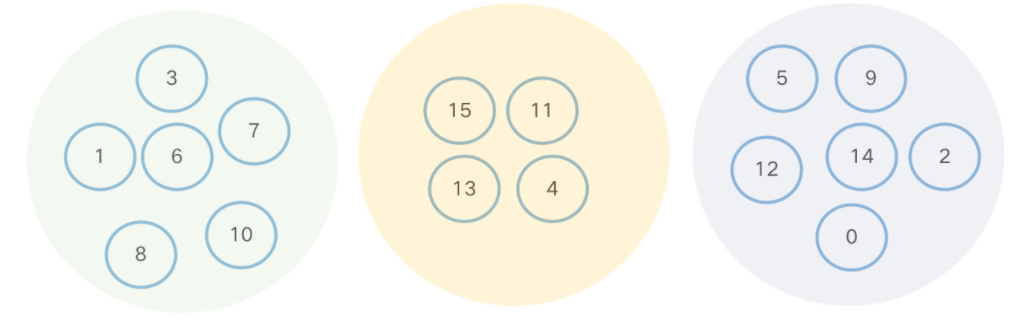
于是我们可以这样概括性地描述并查集：

并查集 (不相交集) 是一种描述不相交集合的数据结构，即若一个问题涉及多个元素，它们可划归到不同集合，同属一个集合内的元素等价（即可用任意一个元素作为代表，比如上述的互为亲戚即互相等价），不同集合内的元素不等价。

这基本上就是对并查集的完整描述了，十分简单。问题涉及的元素初始时总是自己构成一个单元素集合，求解问题需要通过合并操作将等价元素归入一个集合中。为了能够合并等价元素，我们必须查询希望合并的对象元素属于哪个集合，以决定是否要执行合并。因此 主要操作就是「查询」与「合并」 (注意，此刻我们当然还不知道如何查询如何求并，但并不妨碍我们看出这两个操作的必要性) 。

「不相交」描述的是问题元素构成集合之后各个集合不相交的状态，「并查」描述的是处理问题时的操作。后文中两种称呼都会出现。

上面的亲戚问题只用于引入并查集的概念，而本文剩下的内容，会以 547: 省份数量 问题为研究对象，一步步 发明并查集 以解决该问题。

LeetCode 547. 省份数量
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。
省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例1:
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
示例2
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

不难看出这是一个典型的并查集问题。如果我们能够通过矩阵信息将同一省份的城市都加入到同一个集合，最终有多少个省份就会有多少个不相交集合。

从现在开始，行文视角换成正在读本文的你。对于上述问题，你在草稿纸上稍作勾画，写下了如下处理过程 (draft版)：

1. 初始时，每个城市是否与其他城市同属一省是未知的，此时每个城市构成单元素集合。

2. 为了知道哪些城市同属一省，需要遍历矩阵，若 $(i, j)$ 为 1，说明 $i, j$ 两个城市同属一省，可以合并在一起，得到一个 2 元素集合。在集合扩大的过程中，需要找到一个代表，以便多元素集合之间的合并。即当询问 $i$ 与 $j$ 是否应当合并时，需先确定 $i$ 和 $j$ 各自的代表，若相同，那么她们在之前就已经通过其他城市合并在一起了，若不同，则合并之，即向其中一个城市宣告它的代表，使她可以知道自己属于哪个省。现在，「查询」与「合并」变得更具体了。

3. 对未确定归属的城市进行上述的查询合并操作，当结束矩阵遍历时，所有城市就都知道了自己的代表。此时再遍历一遍所有城市，「查询」她们的代表，有多少个不同的代表，就有多少个不同的省份，于是问题得到解决。

通过上述对处理过程的思考，你发现 「代表」 在这一过程中至关重要，且所谓「同属一省的城市 (形成了集合) 」并不是静态的将这些城市放在了一起（放到表中或者其他什么静态的数据结构中），而是 动态地 查询它们的代表才知道的。一个迫切要解决的问题就是如何保存及表示「代表」。再回顾一遍查询操作，假设集合中的某个元素 (省会城市) $x$ 为该集合的代表，查询城市 $y$ 是否属于 $x$ 所在的省时，虽然不能直接得知这一信息，但 $y$ 可能知道自己与其他城市是否在同一省，而这个其他城市又知道自己与 $x$ 在同一省，或者经过「若干跳」来追溯到 $x$ ，那么你就能够知道 $y$ 与 $x$ 为同一省。这种向着一个方向串联的关系使你立刻想到以 (单向) 链表 来实现 (这是你的独创，虽然后面你会知道用树的概念更合适，但谁让你现在还 一无所知 呢)。于是你将每个城市想象成单向链表中的一个结点，以尾节点 (省会城市) 作为代表，每个元素 (城市) 指向它的后继 (通过矩阵中的 1 得知) ，连续地向 $next$ 查询，一定能查询到尾结点。查询两个节点元素的尾结点是否相同，即可知道他们是否属于同一集合。你有了「查询」的感觉，并且当你思考「合并」操作时，也隐隐感觉到也许可以通过改变链表指针来实现，但你还不确定。

总之，你勾勒出了并查集处理问题的主要过程为： 初始化 (单元素集合) 、合并和查询 。不待稍歇，你即刻拍马上路。

处理过程

初始化

你首先尝试完成 初始化 。虽然前面你有了链表的方案，但你更希望从最简单的 (实际上也是最常用的) 的数据形式入手，如果也能实现那当然更好。于是你采用了 0 到 $n - 1$ 的整数代表问题涉及的 $n$ 个元素，并以 数组 储存之。自然地，下标即代表元素，值为与该元素有 「等价」 关系的元素，效果上等于你之前链表想法中结点的 $next$ 指针 (引用) ，看起来能行。在亲戚关系中该等价关系为是否互为亲戚，在省份问题中等价关系为是否同属一省。对于省份问题，你创建了一个 $capital[]$ 数组 ( $capital$ 即省会，虽然对于城市 $i$， $capital[i]$ 是与 $i$ 在矩阵中有「联系」的城市， 不一定是省会，但你想不到更好的数组名，变量命名是你一生的课题 ，暂时就这样吧)， $capital$ 大小为输入矩阵的一维长度，即城市数量。初始时，每个元素只知道 自己与自己「等价」 ，因此创建这个数组后，遍历并使得 $capital[i] = i$ 。这样初始化就完成了，看起来十分 OK👌。

// 初始化
int[] capital = new int[isConnected.length];
for(int i = 0; i < isConnected.length; i++) {
    capital[i] = i;
}

编写代码解题时，初始化过程可以在主方法中完成，也可以在并查集类 $UnionFind$ 的构造器中完成。你选择在构造器中完成初始化，并写下如下代码。

class Solution{
    // 在主方法(findCycleNum)中new UnionFind
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        UnionFind uf = new UnionFind(isConnected); // 通过构造器完成初始化
  
        // 求解过程 ???
  
        return ???;
    }
}

// UnionFind类，只写我们当前知道的。
class UnionFind{
    private int[] capital;
    // 其他字段???
    
    public UnionFind(int[][] isConnected){ // 构造方法
        this.capital = new int[isConnected.length];
        for(int i = 0; i < isConnected.length; i++){ 
            capital[i] = i;
            // 其他字段的初始化???
        }
    }
}

接着你写了个输入矩阵，一共有 6 个城市 $\{0, 1, 2, 3, 4, 5\}$ ，isConnected[i][j] = 1 表示 $i$ 与 $j$ 为同一省。

// 输入矩阵M
{
{1, 0, 0, 0, 1, 0}, // 0-0, 0-4
{0, 1, 0, 0, 0, 1}, // 1-1, 1-5
{0, 0, 1, 1, 0, 1}, // 2-2, 2-3, 2-5
{0, 0, 1, 1, 0, 0}, // 3-2, 3-3
{1, 0, 0, 0, 1, 0}, // 4-0, 4-4
{0, 1, 1, 0, 0, 1}, // 5-1, 5-2, 5-5
}

初始化后得到如下 5 个单元素集合。

合并

你现在开始尝试实现 合并方法 ($union$) 。在你设计的处理过程中已经写到，合并的依据是查询，你先假设自己已经实现了「查询」方法 $find(x)$ ，该方法返回 $x$ 的当前代表。合并 $x$ 和 $y$ 的前提是 find(x) != find(y) ，因为若 find(x) == find(y) ，说明二者已经在同一集合中了（同一省）。具体做法如下，对于 $x$，$y$ 两个城市，若 find(x) != find(y) ，就令 capital[find(y)] = find(x) ，当然也可以是 capital[find(x)] = find(y) ，选用其中一种即可。你一开始可能想要写成 capital[x] = y，但马上发现这么写只能表示 $y$ 是 $x$ 的代表，而你的目的是用 $y$ 目前的代表 ( $find(y)$ 的返回值) 来作为 $x$ 的代表 ( $find(x)$ 的返回值) 的代表，这样才能使得 $x$ 目前的集合 整体并入 $y$ 所在的集合。

到这你停顿了一下，又强调着提醒了一下自己，这里的「合并」并非真的把元素「静态地」装到了一个什么数据结构中，而是要通过 $find$ 才知道某个元素属于哪个集合，所以「合并 $x$ 与 $y$ 」就是「把 $y$ 所在集合合并到 $x$ 所在集合中」，也就是 「使 $y$ 所在树的根指向 $x$ 所在树的根」 ，这样以后查询原 $y$ 所在集合的任意元素，指向原根后，会继续指向 $x$ 所在集合的根，也就知道此时这些元素已经合并到 $x$ 所在集合中了（在实现查询方法后你会有更深的体会）。合并方法就这么实现好了，并不复杂，你的信心开始上涌。

// union方法
public void union(int x, int y) {
    if(find(x) != find(y)){
        capital[find(y)] = find(x); // 令 x 的代表作为 y 的代表的代表
    }
}
// 在main方法中遍历矩阵，调用union执行合并的过程的写法如下：
for(int i = 0; i < n; i++){
    for(int j = i + 1; j < n; j++){
        if(isConnected[i][j] == 1) uf.union(i, j);
    }
}

于是主方法扩充为如下：

class Solution{
    // 在主方法(findCycleNum)中new UnionFind
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        UnionFind uf = new UnionFind(isConnected); // 通过构造器完成初始化
        // 两个for，遍历矩阵完成合并
        for(int i = 0; i < n; i++){
            for(int j = i + 1; j < n; j++){
                if(isConnected[i][j] == 1) uf.union(i, j);
            }
        }
        return ???; // 完成合并后我们已经完成求解，但现在还不知道该返回什么
    }
}

现在你想试试这个合并方法能不能有效处理输入矩阵，并看看会「合并」成何种状态。为方便，你把前面的输入矩阵 $isConnected$ 再一次写在这里。 遍历前三行，你画出了遍历到 $isConnected[2][3]$ 和 $isConnected[2][5]$ 的状态（建议动手画一下，加深理解）。可以看到，遍历前三行后，就已经得到了最终的两个不相交集，所以对于这个输入，一共有两个省。

// 输入矩阵M
{
{1, 0, 0, 0, 1, 0}, // 0-0, 0-4
{0, 1, 0, 0, 0, 1}, // 1-1, 1-5
{0, 0, 1, 1, 0, 1}, // 2-2, 2-3, 2-5
{0, 0, 1, 1, 0, 0}, // 3-2, 3-3
{1, 0, 0, 0, 1, 0}, // 4-0, 4-4
{0, 1, 1, 0, 0, 1}, // 5-1, 5-2, 5-5
}

当你画出 $union$ 的过程后，自然地发现，数据的结构呈现出 「树」 的形态，原先的单向链表的「尾结点」为树的 「根」 ，但与通常的树不同，这里的链接关系是从孩子结点指向父结点。现在，你非常自然地将并查集结构从一开始的「单向链表」转换成了「树」。

※ 作者按：我认为用树来理解不是特别重要，这个结构按链表理解完全没问题，一个「集合」也可以描述成一条或多条相交于尾结点的链表，「尾结点」等同于树中的「根」，后续出现的「树高」的概念也可以说是「最长链」的长度等等，只不过确实不如树的形象和树的语言描述来得方便。总之后续转换为树的语言来描述这里的「集合」）。

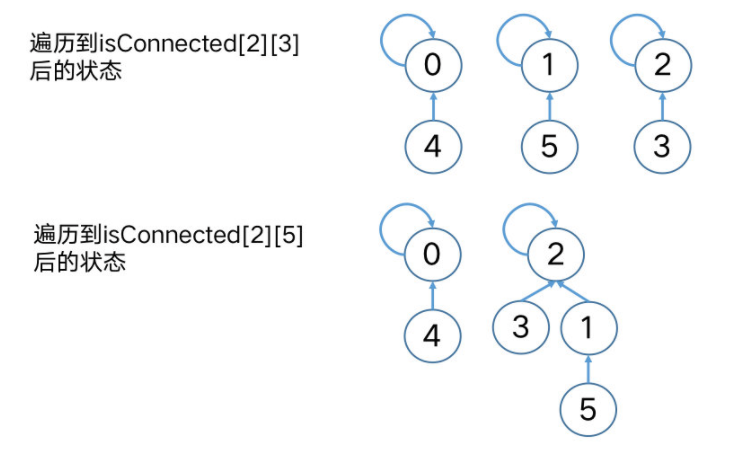
再谈合并语句

前面我们说到 $union(x,y)$ 是要将 $y$ (或 $x$ ) 所在树的根指向 $x$ (或 $y$ ) 所在树的根，因此要写成 capital[find(y)] = find(x) (或 capital[find(x)] = find(y) ) 。现在我们具体看看为什么 capital[y] = x 这样的写法为什么是错误的。如下所示的两个三元素集合，1 为 $\{1,2,3\}$ 的根，4 为 $\{4,5,6\}$ 的根。以 $capital[y] = x$ 执行 $union(3, 5)$ ，那么两棵树会合并，合并后 $find(2)$ 和 $find(6)$ 查到的根分别是 1 和 4 ，所以当询问 2 和 6 是否在同一集合时会出错。读者朋友们可以把「小结」中的代码的 capital[find(y)] = find(x) 改成 capital[y] = x ，实际验证后会发现确实无法通过该题。

    1          4      
   / \        / \
  2   3  <-  5   6    

查询

你现在开始尝试实现 查询方法 ( $find$ 方法) 。之前已经说过，若集合以单向链表（暂时还用链表的语言描述）的形式组织，尾结点为集合代表 (省会)。那么查询应该是一个递归的过程，熟悉链表写法的你立即写出如下 尾递归 代码。

※ 当然也可以用迭代来实现，这里采用递归方式实现，后续你会知道用递归而非迭代实现的好处。

// 如果用链表组织集合，find可实现如下
public Node find(Node x){
    if(x.next == null) return x;
    return find(x.next);
}

这相当理想，不过别忘了，虽然将集合想象成链表，但目前 $capital$ 是一个数组，要怎样沿着 $x$ 到找到它的代表元呢？如果做不到这一点你很可能要回到初始化推倒重来了。想到这里，你意识到要先思考此时该 如何找到代表元 。初始化单元素集合时，capital[i] = i ，如果此时合并 $i$ 和 $j$ ，令 capital[find(j)] = find(i) ，因为刚开始 find(j) = j ，find(i) = i ，所以这个合并其实就是 capital[j] = i ，并且要令此后 find(j) = i 。你发现，代表元的特点是 find(i) = i ，即自己指向自己，而非代表元 find(j) = i ( $i$ 是 $j$ 的代表) 不具备这个特点。于是仿照前面链表的写法，你轻松写出如下 $find$ 方法。当 capital[x] = x 时，找到代表元，否则就找当前代表元的代表元，因为从 $x$ 到它的代表元，一定是串联在一条链上的，而对于尾结点 $t$ ，一定满足 capital[t] = t ，因此可以保证找到 $x$ 的代表元 $t$ 。可以看到，无论是 $union$ 还是 $find$ ，无论从理解上还是从实现上，都异常简单（这正是并查集的一大特色，短小精悍，以少量的代码完成高效的处理，你后续还会反复体会到这一点）。

// find方法
public int find(int x) {
    if(capital[x] == x) return x; // 只有根节点满足capital[x] = x
    return find(capital[x]);  
}

小结

至此你得到了基本的并查集实现，主要方法 $find$ 和 $union$ 都只有数行代码，十分简洁。你回顾了一下刚才的实现，写下如下概括性的总结。

• 初始化： 初始化代表下标 $i$ (城市 $i$ ) 的省会 ( $capital[i]$ ) 的 $capital$ 数组，一开始令 capital[i] = i 。
• 合并： 以查询为基础，$union(x, y)$ 将 $y$ 当前的代表元「指向」 $x$ 当前的代表元。
• 查询： 为尾递归方法，$find(x)$ 不断在链上沿着 $x$ 到它的代表元的方向前进，直到找到代表元(尾结点)。

现在，你已经 「独立发明」 了基本并查集，写下如下代码，并验证了它确实能够解决省份问题，你感到一阵兴奋。

※ 最终的省份数量可以在合并完成后对所有元素执行一次 $find(x)$ ，统计不同结果的个数得到。更聪明的做法是设置一个 unionCount = 0 ，表示合并的次数，在 $union$ 方法内添加一行代码，使得发生合并时 unionCount++ 实现累计，最后元素总数减去合并次数即为不相交集数量，也即省份数量。

class Solution{
    // 在主方法(findCycleNum)中new UnionFind
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        UnionFind uf = new UnionFind(isConnected); // 通过构造器完成初始化
        // 两个for，遍历矩阵完成合并
        for(int i = 0; i < n; i++){
            for(int j = i + 1; j < n; j++){
                if(isConnected[i][j] == 1) uf.union(i, j);
            }
        }
        return n - uf.unionCount; // 完成合并后我们已经完成求解，但现在还不知道该返回什么
    }
}

// UnionFind类，只写我们当前知道的。
class UnionFind{
    private int[] capital;
    int unionCount = 0; // 合并次数
    public UnionFind(int[][] isConnected){ // 构造器
        this.capital = new int[isConnected.length];
        for(int i = 0; i < isConnected.length; i++){ 
            capital[i] = i;
        }
    }
    // union方法
    public void union(int x, int y) {
        if(find(x) != find(y)){
            capital[find(y)] = find(x);
            unionCount++; // 实时统计合并次数
        }
    }
    // find方法
    public int find(int x) {
        if(capital[x] == x) return x; // 只有根节点满足capital[x] = x
        return find(capital[x]);  
    }
}

治学十分严谨的你开始研究目前的实现，并思考这一基本实现是否存在什么问题，或者有什么可以优化的地方。你首先从数据规模上考虑，若元素较多时，你发现将得到一条很长的链，对头节点查询其代表元时，需要遍历整条链。例如上述 $\{1, 2, 3, 5\}$ 这个集合，如果还有 $\{6\}, \{7\}, \{8\}$ 这三个单结点元素，且令 $\{1, 2, 3, 5\}$ 连续地与它们合并，即执行 $union(6, 5), union(7, 5), union(8, 5)$ 之后，得到如下。

※ 对于本题，因为只需要遍历矩阵右上三角执行合并，因此 $union(x,y)$ 总有 $x > y$ ， 上述 $union(6, 5), union(7, 5), union(8, 5)$ 实际上并不会执行，这么写只是为了引出后续内容而设置的假想情形。不过，在别的题目中，若 $union(x, y)$ 时， $x$ 总是一个单元素集合的话，是完全有可能出现链状树的。

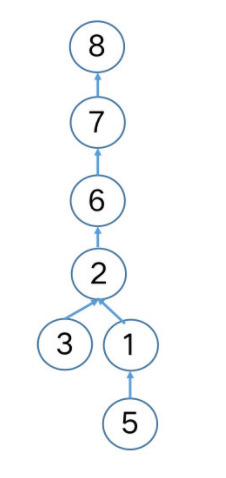
你发现，简单直接的合并将导致较高的树，若再继续执行 $union(5, 9)$ ，首先进行的 $find(5)$ 将会依次向父节点方向查询 $1, 2, 6, 7, 8$ ，查询效率低下。设想，如果能将树的高度降低，例如除根节点外的所有节点直接挂在根节点下（ 放射状 ，或者也有人说是 菊花状 ），那么 $find$ 的复杂度将为常数级，$union$ 也会因此变为常数级操作。基于这个思考，你将在下一节继续发明更好的求并方法，使得两棵树合并后得到的新树拥有更低的树高。

补充说明：寻找等价关系

在省份数量问题中，矩阵已给出等价信息，使得我们可以直接遍历 $isConnected[i][j]$ ，根据其值是否为 1 来直接求并，但对于有的问题，开始时等价信息并不明显，需要先找到这样的等价关系，然后才能求并。例如 128: 最长连续序列 问题，可以用并查集求解，但需要在开始时对 $i$ 和 $i+1$ 执行一次合并操作，这个「等价」是不太明显的。具体过程（代码）可参考后续内容。

求并优化

以目前的实现求解省份数量问题，你已经发现，合并 $x$ 和 $y$ 所在树 (集合) 时，只是简单地将 $y$ 所在树的根指向 $x$ 所在树的根 $capital[find(y)] = find(x)$ ，最坏的情况下将得到一棵链状的树，较高的树高将导致较高的查询 (及合并) 复杂度。你希望以某种策略使合并后得到树高较小的树。几乎不费思忖，你就得到了一个自然的想法：在合并时，不再默认将 $y$ 所在树 (的根) 挂到 $x$ 所在树 (的根) 上，而是先 比较这两棵树的大小 ，让较小的树挂到较大的树上，因为 较小的树的树高总是倾向于较低 。如果较小的那棵树低于较大的那棵树，合并后树高不变！你迫不及待继续码起来。

按大小求并

现在，你尝试实现这种 「按大小求并」 的做法。这很简单，只需要在合并前比较两棵树的大小即可，如下，「按大小求并」的 $union$ 方法对你来说就是「分分钟」（此时你已经有点膨胀了，不过作为并查集发明人，倒也不为过）。（为了从更广泛的意义上描述，此后不再特别强调「省份数量」问题，且把 $capital$ 数组改为更一般的 $parent$ 数组，表示父结点。）

※ 用 $parent$ 而不是 $father$ ，就像说孩子结点而不是儿子结点，用 $child$ 而不是 $son$ ，都是名称上的性别正义，不过中文语境中很少说“亲结点”，因此还是描述为父结点。

// Union方法：按大小求并
public void union(int x, int y){
    int xRoot = find(x), yRoot = find(y);
    // 根节点不同才求并
    if(xRoot != yRoot) {
        if(size[yRoot] <= size[xRoot]){ // 当y所在树大小小于等于x所在树大小时
            parent[yRoot] = xRoot; // 将yRoot挂在xRoot上
            size[xRoot] += size[yRoot]; // 更新x所在树的大小
        } else {
            parent[xRoot] = yRoot;
            size[yRoot] += size[xRoot];
        }
    }
}

你新增了一个与 $parent$ 大小相同的 $size$ 数组，$size[i]$ 表示 $i$ 结点所在树的大小。$UnionFind$ 类中需要添加 $size$ 数组字段和相应的初始化内容（单结点集合的大小为 1）。如下代码在构造器中初始化树大小数组 $size []$ 。补充后如下，并且你稍微修改了构造器的入参，不是以矩阵为入参，而是以一维数组为入参， $parent$ 数组的初始化改为写在主方法中。因为你觉得这样有利于使 $UnionFind$ 类的写法统一且稳定，不必总是对不同问题进行调整。你对这一修改还算满意。

// 初始化
int[] parent = new int[isConnected.length];
for(int i = 0; i < isConnected.length; i++) {
    parent[i] = i;
}
UnionFind uf = new UnionFind(parent);

// UnionFind类(部分)
class UnionFind{
    private int[] parent, size; // size保存树的大小
    public UnionFind(int[] parent) {
        this.parent = parent;
        this.size = new int[parent.length];
        for (int i = 0; i < parent.length; i++) {
            this.size[i] = 1; // 初始时单节点树大小为1
        } // 或者 Arrays.fill(size, 1);
    }
}

按大小求并的方法就这样实现出来了。不过在欣赏这个实现之余，你难免会回想自己当初 为何出发 ，起初你希望合并后的树拥有较低的树高，但是一棵大小较小的树完全有可能高于大小较大的树，比如链状树在结点较少时也很容易高于菊花树。那为何不直接按高度求并呢？而且按高度求并还有一个好处，新树的高度变化只发生在两棵树高度相等时，此时高度加 1 ，而按大小求并时，每次合并都要修改新树的大小。沿着这个想法，下一节你将继续发明 「按高度求并」。

按秩(高度)求并

不是「按高度求并」吗，怎么还有个 「秩 ( $rank$ ) 」 ？现说明如下，但该说明的内容你只能在下一节发明「路径压缩」后才会理解，此处按下不表，你可以先将「秩 ( $rank$ )」暂时等同于「高度 ( $height$ ) 」。

当并查集的查找方法不具有「带路径压缩」的效果时，本节所述方法就是严格的「按高度求并」。

当并查集应用了「带路径压缩」的查找方法时，$height$ 将不能表示严格的「树高」的概念，为严谨，需改称「按高度求并」为「按秩求并」。

类似「按大小求并」的做法，你立即写出「按秩 (高度) 求并」的如下方法（初始化 $rank$ 数组写法与 $size$ 数组一致，此处省略。另外下面代码的写法有点不规范，括号内单行语句的情况你都省略了括号，不过你并不是很在意，心想规范个腿，我没写成一行算客气的了）。

// union方法：按秩(高度)求并，先判断是否在同一集合
public void union(int x, int y){
    int xRoot = find(x), yRoot = find(y);
    if( xRoot != yRoot){
        if(rank[yRoot] <= rank[xRoot]) parent[yRoot] = xRoot;
        else parent[xRoot] = yRoot;
        if(rank[xRoot] == rank[yRoot]) rank[xRoot]++; 
    }
}

你敏锐地发现还可以有一种去掉 if(xRoot != yRoot) 判断的写法。因为你发现即便 xRoot == yRoot ，根据 rank[xRoot] == rank[yRoot] ，将执行 parent[yRoot] = xRoot ，仍是根结点指向自己，并未改变什么。在不同集合元素求并操作较多时，这样做可以节省一点 xRoot != yRoot 判断的时间。当然，这并不重要，你只是想多展现一些不同的写法。你还注意到，采用这种写法后，在决定是否要增加秩 (树高) 时，要判断是否有 xRoot != yRoot 。即当两棵树秩 (高度) 相等且为不同集合时，新树的秩 (高度) 加 1。

// union方法：按秩(高度)求并，不判断是否在同一集合
public void union(int x, int y){
    int xRoot = find(x), yRoot = find(y);
    if(rank[yRoot] <= rank[xRoot]) parent[yRoot] = xRoot;
    else parent[xRoot] = yRoot;
    if(rank[xRoot] == rank[yRoot] && xRoot != yRoot){
        rank[xRoot]++; 
    }
}

秩 (高度) 较小的树的秩 (高度) 无需更新，因为每次求一个元素所在集合的高度都会先找到该集合的树的根，秩 (高度) 较小的树在合并后其树根在新树中就不是树根了。这一点你当然了若于胸。

现在你回过头重新审视前述导致树高较高的基本合并方法，并尝试使用优化的「按秩 (高度) 合并」方法看看效果。对于 $\{1, 2, 3, 5\}$ 集合，连续地合并它与单节点集合 $\{6\}, \{7\}, \{8\}$ ，即执行 $union(6, 5), union(7, 5), union(8, 5)$ ，在应用按秩 (高度) 求并之后，得到如下。

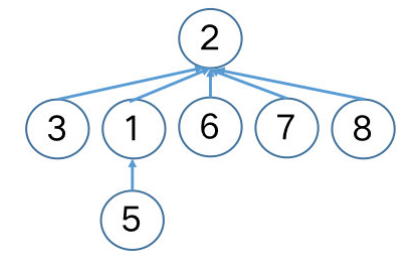
效果十分理想。但结点 5 显得异常扎眼，如果能将节点 5 也直接连到根节点 2 下，将得到最完美的高度为 2 的树。这是否能做到呢？一番踌躇后，你发现在 $union$ 方法中无法做到这一点，因为 $union$ 的作用只是让一个树根指向另一个树根。那 $find$ 方法能实现吗？勤学好问的你继续逼问自己，并想到 $find(5)$ 从 5 沿着父结点方向走向根，看起来可以在这个过程中做些文章。于是，你再接再厉，在下一节中继续这一优化。如果实现该优化，将使得 5 到根结点 2 的路径缩短，因此你在这里提前把这个优化命名为 「路径压缩」，优化后的 $find$ 方法称作 「带路径压缩的查找」。

路径压缩

前面提到，在 $find(5)$ 时，如果能在查询过程中将 5 的父结点改为 2，就完成了「路径压缩」，熟悉递归的你立刻感觉到这很容易，只需在 $find$ 方法中修改一行代码，就可以让 $find$ 在查询根节点的同时执行这个「压缩」的操作。于是你写下如下代码，改动了 $return$ 语句，将递归的 $find[parent[x]]$ 赋值给 $parent[x]$ ，如下。略作推敲，你肯定该写法正确无误，可以让 当前查找的节点到根节点路径上所有的节点都指向根节点 。

// find方法：带路径压缩
public int find(int x) {
    if(parent[x] == x) return x;
    return parent[x] = find(parent[x]);  
}

你继续审视前述按秩 (高度) 合并的扎眼的 5 ，在更新了「带路径压缩」的 $find$ 方法后，重新执行一次 $union$ 看下会发生什么。对 $\{1, 2, 3, 5\}$ 集合，连续地与单节点集合 $\{6\}, \{7\}, \{8\}$ 合并。首先执行 $union(6, 5)$ ，方法内会执行 $find(5)$ 来查找5的根结点，在带路径压缩的 $find$ 中，5 在寻找其所在树的根节点的过程中，实时地令其到根节点路径上的所有节点都指向了根节点，于是原路径被压缩，继续合并 $\{7\}$ 和 $\{8\}$ 之后你画出下图。

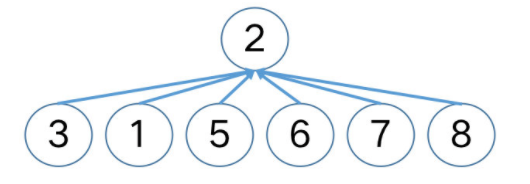
终于得到了一棵对于查询 (以及合并) 来说最完美的树，心情不错的你为防万一，又检查了一遍实现过程，并有一个 不大不小中发现 。5 指向 2 发生在 $union(6, 5)$ 时 (其内调用 $find(5)$ ) ， $find$ 方法不会修改树的高度，「压缩」前后 $rank[2]$ 保持不变，即 $rank[2] = 3$ ，但经过 $find$ 的压缩，树的高度已经变为 2 了。这时你突然有所领悟，原来这就是称做「按秩求并」而非「按高度求并」原因。一声「なるほど」之后你快速写下如下总结（「好记忆不如烂笔头」是你小学三年级的座右铭，你还把这句话刻在了书桌右上角）：

「按秩求并」而非「按高度求并」：

在应用带路径压缩的查询和按秩求并后，$rank[root]$ 记录的数字是树实际高度的一个上界，树的实际高度可能小于此值。

对于「秩 ( $rank$ )」，你还有这样的思考: 按高度求并的优化原本是用「高度 ( $height$ )」来指导树的合并，但因为 「同时」 应用了 「路径压缩」 优化，导致程序记录的 $height$ 信息不再是严格定义下的「高度」，这就好像树高被 $find$ 给压缩了，但 $height$ 这个变量没察觉到这个变化，导致 $height$ 不再能表达「真实高度」。因此为了严谨，我们不能再使用 $height$ 这个单词 (这个概念) ，转而采用另一个词 (另一个概念) 来指代此时的「高度」。找啊找，发现 $rank$ 这个单词很合适。中文的「秩」是「$rank$」这个词的翻译，就是我们理解的「排名」那样，指一种「不精确的突出相对意味的大小」，Webster 词典对 $rank$ 的第一条释义为: relative standing or position。你当然也可以选择别的词来形容，比如 almost height, rough height 之类的，只不过都不如 $rank$ 更合适。

至此，你完成了一个中等偏大的成就：先是独立发明基本并查集，再通过观察树的形态发现优化方向，主动提出优化方案，并最终实现了两种求并优化（「按大小求并」和「按秩求并」）和一种查询优化（「带路径压缩的查询」）。你略感激动，但也没有四下声张，只是把尚未完稿的文章分享给了一个朋友，还顺手编辑了一张喵喵表情，「并查集，就这？就这？」。

※ Webster词典中给出的 「$rank$ (秩) 」 一词的释义。

类的实现代码

现在你作为并查集发明人，继续总结如下内容。

通过上述对实际问题处理过程的讲解，我们已经给出了能够处理集合代表元查询及合并问题的并查集数据结构。在按大小或按秩求并时，需要保存大小或秩 (高度) 信息的数组。现给出如下包含 直接求并，按大小求并，按秩求并，直接查询，带路径压缩查询 等方法的实现。实际使用时只需按需选择一种求并和一种查询方法即可，按秩求并 + 带路径压缩查询 的组合在多数情况下因其效率更高而成为首选。

class UnionFind{
    private int[] parent, rank, size; // 实际代码中，按秩求并和按大小求并选择其一
    public UnionFind(int[] parent) {
        this.parent = parent;
        this.rank = new int[parent.length];
        this.size = new int[parent.length];
        Arrays.fill(rank, 1); // 实际代码中，按秩求并和按大小求并选择其一
        Arrays.fill(size, 1); // 实际代码中，按秩求并和按大小求并选择其一
    }
    // 直接查找
    public int findDirect(int x) {
        if(parent[x] == x) return x;
        return findDirect(parent[x]);
    }
    // 带路径压缩的查找
    public int find(int x) {
        if(parent[x] == x) return x;
        return parent[x] = find(parent[x]);
    }
    // 直接求并
    public void unionDirect(int x, int y) {
        int xRoot = find(x), yRoot = find(y);
        if(xRoot != yRoot){
            parent[yRoot] = xRoot;
        }
    }
    // 按大小求并
    public void unionBySize(int x, int y){
        int xRoot = find(x), yRoot = find(y);
        if(xRoot != yRoot) { // 根节点不同才求并
            if(size[yRoot] <= size[xRoot]){
                parent[yRoot] = xRoot;
                size[xRoot] += size[yRoot];
            } else {
                parent[xRoot] = yRoot;
                size[yRoot] += size[xRoot];
            }
        }
    }
    // 按秩求并
    public void union(int x, int y){
        int xRoot = find(x), yRoot = find(y);
        if( xRoot != yRoot){
            if(rank[yRoot] <= rank[xRoot]) {
                parent[yRoot] = xRoot;
            } else {
                parent[xRoot] = yRoot;
            }
            if(rank[xRoot] == rank[yRoot]) {
                rank[xRoot]++;
            }
        }
    }
}

无需大小/秩数组空间的技巧

你还在一本书上学到一种技巧，并搬运到了自己的教程上。如果元素的表示不涉及负数（通常如此）的话，可以用一个小技巧来节省大小或秩数组的开销。在以前的说明中，初始化集合时，我们令每一个元素的父节点指向自己，即 parent[x] = x ，表示这是根节点。本技巧以 parent[x] < 0 表示根节点，初始时所有结点不再指向自己，而是置为 -1 ，即 parent[i] = -1 。这样的可行之处在于，$find(x)$ 会一直递归找到根，除了根的 $parent[root]$ 为负数，其他元素 $y$ 的 $parent[y]$ 都是真实存在的父结点的下标，下标自然是非负数。需要注意的是，因其为负数，在两棵树比较大小或秩(高度)时，值越小，则大小或秩 (高度) 越大。在按大小求并时， $size[root]$ 的更新方法不变，但在按秩 (高度) 求并时，新树高度增高 1 时需令 rank[root]-- 。

应用此技巧，给出如下完整实现。同样地，实际使用时只需按需选择一种求并和一种查询方法即可。

※ 此技巧学习自Weiss的 数据结构与算法分析：Java语言描述 。另外，在不用负数技巧的版本中，由于根节点相同不影响结果，考虑到在不同集合元素求并操作较多时，在 $union$ 方法中可以省去 xRoot != yRoot 的判断。这个版本中，必须要执行 xRoot != yRoot 的判断，否则当两个同集合元素比较时，将使得 parent[xRoot] = xRoot ，也即原为一个负数的 parent[xRoot] 的值变成了一个非负数 ( $xRoot$ ) ，将导致程序错误。

/**
 * 应用负数技巧的并查集
 */
class UnionFind2{
    private int[] parent;
    public UnionFind2(int[] parent) {
        this.parent = parent;
    }
    // 直接查找
    public int findDirect(int x) {
        if(parent[x] < 0) return x; // 只有代表元满足 parent[x] < 0
        return findDirect(parent[x]);
    }
    // 带路径压缩的查找
    public int find(int x) {
        if(parent[x] < 0) return x;
        return parent[x] = find(parent[x]);
    }
    // 直接求并
    public void unionDirect(int x, int y) {
        int xRoot = find(x), yRoot = find(y);
        if(xRoot != yRoot){
            parent[yRoot] = xRoot;
        }
    }
    // 按大小求并
    public void unionBySize(int x, int y){
        int xRoot = find(x), yRoot = find(y);
        if(xRoot != yRoot) { // 根节点不同才求并
            if(parent[xRoot] <= parent[yRoot]){ // 负数比较，较小者树较大，xRoot所在树更大(或相等)
                parent[xRoot] += parent[yRoot]; // 更新树的大小
                parent[yRoot] = xRoot;
            } else {
                parent[yRoot] += parent[xRoot];
                parent[xRoot] = yRoot;
            }
        }
    }
    // 按秩求并
    public void union(int x, int y){
        int xRoot = find(x), yRoot = find(y);
        if(xRoot != yRoot) {
            if(parent[xRoot] < parent[yRoot]){ // xRoot所在树秩更大，yRoot挂到xRoot之下
                parent[yRoot] = xRoot;
            } else if(parent[xRoot] > parent[yRoot]){ // yRoot所在树秩更大，xRoot挂到yRoot之下
                parent[xRoot] = yRoot;
            } else{ // 秩等大，yRoot挂到xRoot之下
                parent[xRoot]--; // xRoot所在树秩加1 (负数，实际减1)
                parent[yRoot] = xRoot;
            }
        }
    }
}

复杂度分析

这个部分你终于感到力有不逮，严格的 复杂度证明 你看了八遍，最终选择放弃，暂时只能写下如下内容（但你在行文中假装自己知道什么是 反阿克曼函数 ）。

时间复杂度：严格的分析很复杂，省略。带路径压缩的按秩求并的并查集，其查询与合并操作的时间复杂度均为 $O(α(n))$ ( $α(n)$ 表示增长十分缓慢的反阿克曼函数)，对于任何实际的问题的 $n$ ，$α(n)$ 不会超过 5 。因此可以认为此复杂度为 $O(1)$ 。初始化 $parent[] / size[] / rank[]$ 数组的时间复杂度为 $O(n)$ 。

空间复杂度：取决于 $parent[] / size[] / rank[]$ 数组所占空间，为 $O(n)$ 。

实战应用

在「处理过程」中介绍了应用不相交集处理问题的通用过程，如下一些例题中我们将看到，对于不同的具体问题，各步骤的应用是灵活的。

1. 128.最长连续数列。只需在 $find()$ 时以路径压缩方式合并，除给定初始时的等价关系用到主动合并(直接求并)外，不再调用 $union$ 。
2. 547.省份数量。等价关系在输入矩阵中是明显的，只需在 isConnected[i][j] = 1 时主动合并 $union(i, j)$ 即可，$find()$ 中可以不带合并 (路径压缩)，当然也可以带路径压缩以提高效率。
3. 200.岛屿数量。与省份数量问题的输入都是矩阵，但岛屿数量问题的初始时单节点元素是矩阵中的每一个 “1”，而省份数量问题是列(或行)中的每一个元素。
4. 399. 除法求值 和 1631. 最小体力消耗路径 的并查集解法需要一定的问题抽象能力。

以下题目的并查集解法都十分经典，如果你能够想到应用并查集，应用本文介绍的内容，解题应当是轻松愉快的。也一并给出题解，供读者朋友们自练自查。

题目	难度	题解
323. 无向图中连通分量的数目	中等	题解
547.省份数量	中等	题解
200.岛屿数量	中等	题解
695. 岛屿的最大面积	中等	题解
785. 判断二分图	中等	题解
684. 冗余连接	中等	题解
128.最长连续数列	中等	题解
839. 相似字符串组	困难	题解
399. 除法求值	中等	题解
1631. 最小体力消耗路径	中等	题解
==== 持续更新中 ====

🐮🐮🐮
牛啊，你竟然真的看到这里了。

---

文章更新日志

[2022-06-11]

• 「实战应用」中新增「323. 无向图中连通分量的数目」的并查集题解。
• 优化文章可读性，新增若干补充说明。

[2022-06-05]

• 「实战应用」中新增「1631. 最小体力消耗路径」的并查集题解。
• 修改了「实战应用」的展现方式，不再在本帖中直接贴出题解，而以表格形式罗列，给出题解链接。